Java如何實作折半插入排序演算法

排序演算法介紹

排序演算法是透過特定的演算法因式將一組或多組資料依照既定模式進行重新排序。最終序列依照一定的規律進行呈現。

在排序演算法中，穩定性和效率是我們經常要考慮的問題。

穩定性：穩定是指當兩個相同的元素同時出現於某個序列之中，則經過一定的排序演算法之後，兩者在排序前後的相對位置不會改變。

複雜度分析：

（1）時間複雜度：即從序列的初始狀態到經過排序演算法的變換移位等操作變到最終排序好的結果狀態的過程所花費的時間度量。

（2）空間複雜度：就是從序列的初始狀態經過排序移位變換的過程一直到最終的狀態所花費的空間開銷。

常見的排序演算法分為以下幾種：

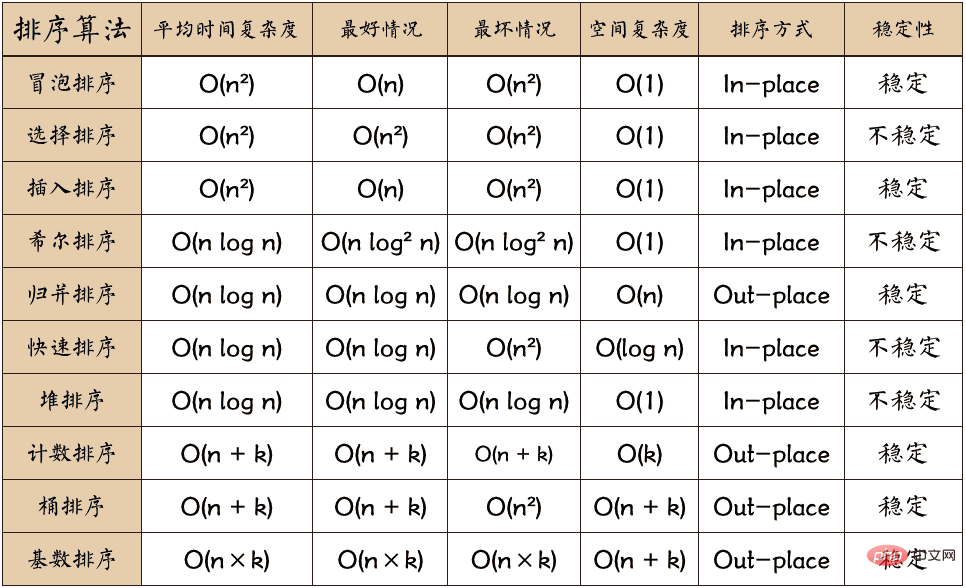
折半插入排序

原理

折半插入排序（Binary Insertion Sort）是插入排序演算法的一種改進。不斷的依序將元素插入前面已排好序的序列中。由於前半部為已排好序的數列，這樣我們不用依序依序尋找插入點，可以採用折半查找的方法來加快尋找插入點的速度。

程式碼實作

在將一個新元素插入已排好序的陣列的過程中，尋找插入點時，將待插入區域的首元素設為a[low] ，末元素設定為a[high] ，則每輪比較時將待插入元素與a[m] ，其中m = (low high)/2 相比較，如果比參考元素小，則選擇a[low]到a[ m-1]為新的插入區域(即high=m-1)，否則選擇a[m 1] 到a[high] 為新的插入區域（即low=m 1），如此直至low

總之：利用已排好的元素有序的特點，使用折半查找的特點來快速找到要插入的位置。

    // Binary Insertion Sort method    
    private static void binaryInsertSort(int[] array){
       
        for(int i = 1; i < array.length; i++){
           
            int temp = array[i];            
            int low = 0;            
            int high = i - 1;  
           
            while(low <= high){                
                int mid = (low + high) / 2;                
                if(temp < array[mid]){                    
                    high = mid - 1;                
                }else{                    
                    low = mid + 1;
                }       
            }
           
            for(int j = i; j >= low + 1; j--){            
                array[j] = array[j - 1];                                                      
            }       
           
            array[low] = temp;       
        }   
    }

複雜度分析

折半插入排序演算法是一種穩定的排序演算法，比直接插入演算法明顯減少了關鍵字之間比較的次數，因此速度比直接插入排序演算法快，但記錄移動的次數沒有變，所以折半插入排序演算法的時間複雜度還是O(n^2)，與直接插入排序演算法相同。

時間複雜度

最好的情況：O(n)。如果元素排序正向有序，開始的時候就直接找到了位置，不需要尋找和移位。

最壞的情況：O(n^2)。如果元素排序反向有序，那麼每次都需要進行資料查找。

平均複雜度：O(n^2)。

空間複雜度：O(1)。僅需幾個儲存空間用於記錄資訊的關鍵單元，即空間複雜度為O(1)。

範例：

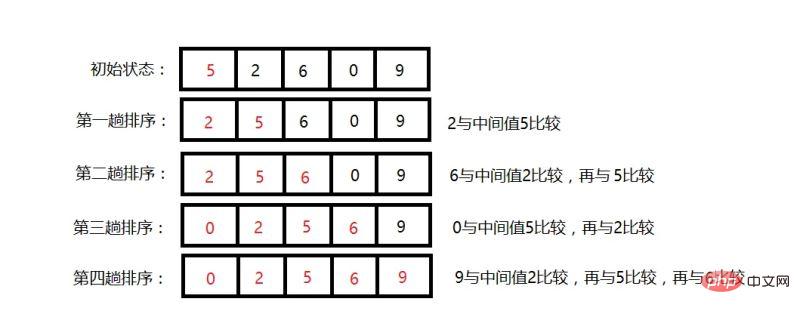
演算法實踐

#演算法的整體想法已經在上面講述了，下面直接使用一個例子來試試水。

折半插入排序

題目描述：

給你一個整數陣列 nums，請你將該陣列升序排列。

範例1：

輸入：nums = [5,2,3,1]

輸出：[1,2,3,5]

範例2：

輸入：nums = [5,1,1,2,0,0]

#輸出：[0,0,1,1,2,5]

提示：

1

-5 * 104

class Solution {
    public int[] sortArray(int[] nums) {
        for(int i = 1; i < nums.length; i++){
           
            int temp = nums[i];            
            int low = 0;            
            int high = i - 1;  
           
            while(low <= high){                
                int mid = (low + high) / 2;                
                if(temp < nums[mid]){                    
                    high = mid - 1;                
                }else{                    
                    low = mid + 1;
                }       
            }
           
            for(int j = i; j >= low + 1; j--){            
                nums[j] = nums[j - 1];                                                      
            }       
           
            nums[low] = temp;       
        }   
        return nums;
    }
}

以上是Java如何實作折半插入排序演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章！