java中並查集的範例分析

一、概述​​

並查集：一種樹型資料結構，用來解決一些不相交集合的合併及查詢問題。例如：有n個村莊，查詢2個村莊之間是否有連接的路，連接2個村莊

兩大核心：

查找(Find) : 找出元素所在的集合

合併(Union) : 將兩個元素所在集合合併為一個集合

二、實作

並查集有兩種常見的實作想法

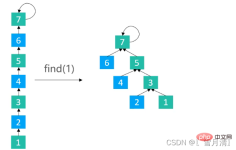
快查（Quick Find）

• 尋找（Find）的時間複雜度：O（1）

• 合併（Union）的時間複雜度：O（n）

快並（Quick Union）

• 找出（Find）的時間複雜度：O（logn）可以優化至O（a（n））a（n）

• #合併（Union）的時間複雜度：O（logn）可以最佳化至O（a（n ））a（n）

使用陣列實作樹型結構，陣列下標示為元素，陣列儲存的值為父節點的值

#建立抽象類別Union Find

public abstract class UnionFind {
 
	 int[] parents;
	/**
	 * 初始化并查集
	 * @param capacity
	 */
	public UnionFind(int capacity){
		
		if(capacity < 0) {
			throw new IllegalArgumentException("capacity must be >=0");
		}
        //初始时每一个元素父节点（根结点）是自己
		parents = new int[capacity];
		for(int i = 0; i < parents.length;i++) {
			parents[i] = i;
		}
	}
	
   /**
     *  检查v1 v2 是否属于同一个集合
     */
	public boolean isSame(int v1,int v2) {
		return find(v1) == find(v2);
	}
 
    /**
     *  查找v所属的集合 （根节点）
     */
	public  abstract int find(int v);
 
	/**
     *  合并v1 v2 所属的集合
     */
	public abstract void union(int v1, int v2);
	
		
	// 范围检查
	public   void rangeCheck(int v)  {
		if(v<0 || v > parents.length)
			throw new IllegalArgumentException("v is out of capacity");
	}
}

2.1 Quick Find實作

以Quick Find實現的並查集，樹的高度最高為2，每個節點的父節點就是根節點

public class UnionFind_QF extends UnionFind {
	public UnionFind_QF(int capacity) {
		super(capacity);
		
	}
 
  // 查
@Override
	public  int  find(int v) {
		rangeCheck(v);
		return parents[v];
	}
 
 // 并 将v1所在集合并到v2所在集合上
@Override
public void union(int v1, int v2) {
    // 查找v1 v2 的父（根）节点
	int p1= find(v1);
	int p2 = find(v2);
	if(p1 == p2) return;
  
    //将所有以v1的根节点为根节点的元素全部并到v2所在集合上 即父节点改为v2的父节点
	for(int i = 0; i< parents.length; i++) {
		if(parents[i] == p1) {
			parents[i] = p2;
		}
	}
	
  }
}

2.2 Quick Union實作

##

public class UnionFind_QU extends UnionFind {
 
	public UnionFind_QU(int capacity) {
		super(capacity);
		
	}
 
	//查某一个元素的根节点
	@Override
	public int find(int v) {
   //检查下标是否越界
		rangeCheck(v);
   
  // 一直循环查找节点的根节点
		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}
 
//V1 并到 v2 中
	@Override
	public void union(int v1, int v2) {
	
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
      //将v1 根节点 的 父节点 修改为 v2的根结点 完成合并
		parents[p1] = p2;
	}
}

三、最佳化

#並且查集常用快並來實現，但是快並有時會出現樹不平衡的情況

#有兩種優化思路：rank優化，size優化 

3.1基於size的優化

核心思想：元素少的樹嫁接到元素多的樹

public class UniondFind_QU_S extends UnionFind{
 
   // 创建sizes 数组记录 以元素（下标）为根结点的元素（节点）个数
	private int[] sizes;
 
	public UniondFind_QU_S(int capacity) {
		super(capacity);
 
		sizes = new int[capacity];
 
   //初始都为 1
		for(int i = 0;i < sizes.length;i++) {
			sizes[i] = 1;
			}
		
	}
 
	@Override
	public int find(int v) {
 
		rangeCheck(v);
 
		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}
 
	@Override
	public void union(int v1, int v2) {
	
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
 
		//如果以p1为根结点的元素个数 小于 以p2为根结点的元素个数 p1并到p2上，并且更新p2为根结点的元素个数
	if(sizes[p1] < sizes[p2]) {
		    parents[p1] = p2;
		    sizes[p2] += sizes[p1];
		
 // 反之 则p2 并到 p1 上，更新p1为根结点的元素个数
	}else {
			parents[p2] = p1;
			sizes[p1] += sizes[p2];
		}
	}
}

基於size優化還有可能導致樹不平衡

3.2基於rank優化

核心思想：矮的樹嫁接到高的樹

public class UnionFind_QU_R extends UnionFind_QU {
   // 创建rank数组  ranks[i] 代表以i为根节点的树的高度
 private int[] ranks;
 
	public UnionFind_QU_R(int capacity) {
		super(capacity);
 
		ranks = new int[capacity];
 
		for(int i = 0;i < ranks.length;i++) {
			ranks[i] = 1;
		}
 
	}
    
	public void union(int v1, int v2) {
 
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
    
    // p1 并到 p2 上 p2为根 树的高度不变
		if(ranks[p1] < ranks[p2]) {
			parents[p1] = p2;
			
  // p2 并到 p1 上 p1为根 树的高度不变
		} else if(ranks[p1] > ranks[p2]) {
			parents[p2] = p1;
 
		}else {
    // 高度相同 p1 并到 p2上，p2为根 树的高度+1
			parents[p1] = p2;
			ranks[p2] += 1;
		}
	}
}

基於rank優化，隨著Union次數的增多，樹的高度依然會越來越高  導致find操作變慢

有三種想法可以繼續優化：路徑壓縮、路徑分裂、路徑減半

#3.2.1路徑壓縮（Path Compression ）

find時使路徑上的所有節點都指向根節點，從而降低樹的高度

/**
 *  Quick Union -基于rank的优化  -路径压缩
 *
 */
public class UnionFind_QU_R_PC extends UnionFind_QU_R {
 
	public UnionFind_QU_R_PC(int capacity) {
		super(capacity);
		
	}
 
	@Override
	public int find(int v) {
		rangeCheck(v);
 
		if(parents[v] != v) {
 
        //递归 使得从当前v 到根节点 之间的 所有节点的 父节点都改为根节点
			parents[v] = find(parents[v]);
		}
		return parents[v];
	}
}

雖然能降低樹的高度，但是實現成本稍高 

3.2 .2路徑分裂（Path Spliting）

使路徑上的每個節點都指向其祖父節點

/**
 *  Quick Union -基于rank的优化  -路径分裂
 *
 */
public class UnionFind_QU_R_PS extends UnionFind_QU_R {
 
	public UnionFind_QU_R_PS(int capacity) {
		super(capacity);
		
	}
 
	@Override
	public int find(int v) {
		rangeCheck(v);
		while(v != parents[v]) {
 
			int p = parents[v];
			parents[v] = parents[parents[v]];
			v = p;
		}
		return v;
	}
}

3.2.3路徑減半（Path Halving）

使路徑上每隔一個節點就指向其祖父節點

/**
 *  Quick Union -基于rank的优化  -路径减半
 *
 */
public class UnionFind_QU_R_PH extends UnionFind_QU_R {
 
	public UnionFind_QU_R_PH(int capacity) {
		super(capacity);
		
	}
	
	
    public int find(int v) {
    	rangeCheck(v);
 
		while(v != parents[v]) {
			parents[v] = parents[parents[v]];
			v = parents[v];
		}
		return v;
	}	 
 }

使用Quick Union 基於rank的最佳化路徑分裂或路徑減半

可以確保每個操作的均攤時間複雜度為O(a(n)) , a(n)

以上是java中並查集的範例分析的詳細內容。更多資訊請關注PHP中文網其他相關文章！