Java實作最小高度樹的方法

題設要求

樹是一個無向圖，其中任何兩個頂點只透過一條路徑連接。換句話說，一個任何沒有簡單環路的連通圖都是一棵樹。

給你一棵包含 n 個節點的樹，標記為 0 到 n - 1 。給定數字n 和一個有n - 1 條無向邊的edges 列表（每一個邊都是一對標籤），其中edges[i] = [ai, bi] 表示樹中節點ai 和bi 之間存在一條無向邊。

可選擇樹中任何一個節點作為根。當選擇節點 x 為根節點時，設結果樹的高度為 h 。在所有可能的樹中，具有最小高度的樹（即，min(h)）稱為 最小高度樹 。

請你找出所有的 最小高度樹 並按 任意順序 返回它們的根節點標籤列表。

樹的 高度 是指根節點和葉節點之間最長向下路徑上邊的數量。

範例1：

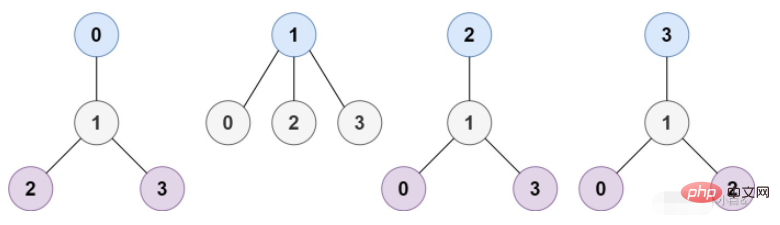
輸入：n = 4, edges = [[1,0],[1,2],[1,3] ]
輸出：[1]
解釋：如圖所示，當根是標籤為1 的節點時，樹的高度是1 ，這是唯一最小的高度樹。

範例2：

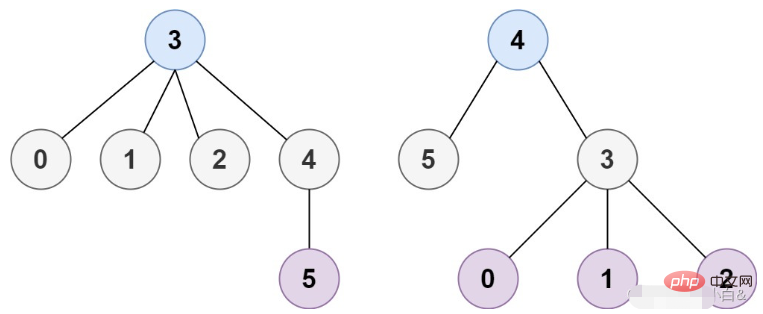
輸入：n = 6, edges = [[3,0],[3,1],[3 ,2],[3,4],[5,4]]
輸出：[3,4]

提示：
1 edges.length == n - 1
0 ai != bi
所有(ai, bi) 互不相同
給定的輸入保證是一棵樹，並且不會有重複的邊

解題思路

  由上述兩個圖我們可以得出結論：題中需要解的是樹裡面的中心節點，而每個樹的中心節點不會超過兩個。

  而我們想要求得樹裡面的中心節點，我們就可以逐層FBS（也就是逐層將出度為一的葉子節點剪掉），直至剪到最後一層，就可以將結果輸出了！

演算法

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        List<Integer> res = new ArrayList<Integer>();
        //如果只有一个节点，则它就是最小高度树
        if(n == 1){
            res.add(0);
            return res;
        }

        //每个节点的邻居数量
        int [] degree = new int[n];
        //每个节点的邻居
        HashMap<Integer,List<Integer>> map = new HashMap<>();

        for(int [] edge : edges){
            int a = edge[0];
            int b = edge[1];

            degree[a]++;
            degree[b]++;

            if(map.get(a) == null){
                map.put(a,new ArrayList<Integer>());//key:节点   value:邻居
            }

            if(map.get(b) == null){
                map.put(b,new ArrayList<Integer>());//key:节点   value:邻居
            }

            map.get(a).add(b);
            map.get(b).add(a);
        }

        //建立队列
        LinkedList<Integer> leafNodes = new LinkedList<Integer>();//表示叶子节点
        //将所有度为1的节点入队
        for(int i = 0;i < degree.length;i++){
            if(degree[i] == 1){
                leafNodes.add(i);
            }
        }

        while(leafNodes.size() > 0){
            res.clear();
            //每一层节点的数量
            int size = leafNodes.size();

            for(int i = 0;i < size;i++){
                int leaf = leafNodes.poll();
                //将当前节点加入到结果集
                res.add(leaf);

                List<Integer> neighbors = map.get(leaf);
                //将出度减一，也就是将最外层的叶子节点剪掉
                for(int neighbor : neighbors){
                    degree[neighbor]--;
                    if(degree[neighbor] == 1){
                        //叶子节点入队
                        leafNodes.add(neighbor);
                    }
                }
            }
        }
        return res;
    }
}

以上是Java實作最小高度樹的方法的詳細內容。更多資訊請關注PHP中文網其他相關文章！