Python實現八種機率分佈公式及資料視覺化教程

機率和統計知識是資料科學和機器學習的核心；我們需要統計和機率知識來有效地收集、審查、分析資料。

現實世界中有幾個現象實例被認為是統計性質的（即天氣資料、銷售資料、財務資料等）。這意味著在某些情況下，我們已經能夠開發出方法來幫助我們透過可以描述資料特徵的數學函數來模擬自然。 「機率分佈是一個數學函數，它給出了實驗中不同可能結果的發生機率。」了解數據的分佈有助於更好地模擬我們周圍的世界。它可以幫助我們確定各種結果的可能性，或估計事件的變異性。所有這些都使得了解不同的機率分佈在數據科學和機器學習中非常有價值。 均勻分佈最直接的分佈是均勻分佈。均勻分佈是一種機率分佈，其中所有結果的可能性均等。例如，如果我們擲一個公平的骰子，落在任何數字上的機率是 1/6。這是一個離散的均勻分佈。但是並不是所有的均勻分佈都是離散的－它們也可以是連續的。它們可以在指定範圍內取任何實際值。 a 和b 之間連續均勻分佈的機率密度函數(PDF) 如下：讓我們來看看如何在Python 中對它們進行編碼：

import numpy as np
import matplotlib.pyplot as plt 
from scipy import stats 
 
# for continuous
a = 0 
b = 50 
size = 5000 
 
X_continuous = np.linspace(a, b, size) 
continuous_uniform = stats.uniform(loc=a, scale=b) 
continuous_uniform_pdf = continuous_uniform.pdf(X_continuous) 
 
# for discrete 
X_discrete = np.arange(1, 7) 
discrete_uniform = stats.randint(1, 7) 
discrete_uniform_pmf = discrete_uniform.pmf(X_discrete)
 
# plot both tables 
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,5)) 
# discrete plot 
ax[0].bar(X_discrete, discrete_uniform_pmf) 
ax[0].set_xlabel("X") 
ax[0].set_ylabel("Probability") 
ax[0].set_title("Discrete Uniform Distribution") 
# continuous plot 
ax[1].plot(X_continuous, continuous_uniform_pdf) 
ax[1].set_xlabel("X") 
ax[1].set_ylabel("Probability") 
ax[1].set_title("Continuous Uniform Distribution") 
plt.show()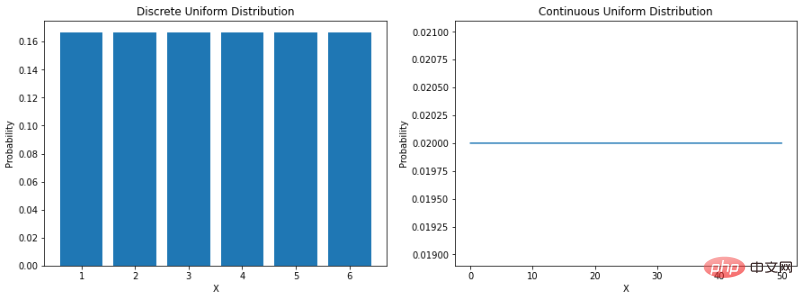

##高斯分佈

高斯分佈可能是最常聽到也熟悉的分佈。它有幾個名字：有人稱它為鐘形曲線，因為它的機率圖看起來像鐘形，有人稱它為高斯分佈，因為首先描述它的德國數學家卡爾高斯命名，還有一些人稱它為常態分佈，因為早期的統計學家注意到它一再發生。常態分佈的機率密度函數如下：σ 是標準差，μ 是分佈的平均值。要注意的是，在常態分佈中，平均數、眾數和中位數都是相等的。當我們繪製常態分佈的隨機變數時，曲線圍繞著平均值對稱——一半的值在中心的左側，一半在中心的右側。並且，曲線下的總面積為 1。

mu = 0 
variance = 1 
sigma = np.sqrt(variance) 
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(x, stats.norm.pdf(x, mu, sigma)) 
plt.title("Normal Distribution") 
plt.show()

對於常態分佈來說。經驗規則告訴我們數據的百分比落在平均值的一定數量的標準差內。這些百分比是：

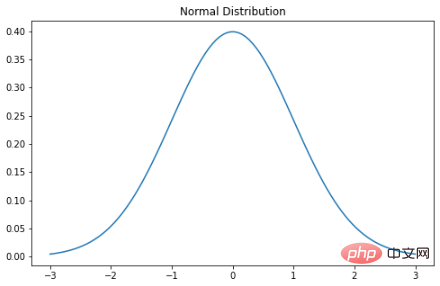
68% 的資料落在平均值的一個標準差內。
• 95% 的資料落在平均值的兩個標準差內。
• 99.7% 的資料落在平均值的三個標準差範圍內。

對數常態分佈

對數常態分佈是對數呈常態分佈的隨機變數的連續機率分佈。因此，如果隨機變數 X 是對數常態分佈的，則 Y = ln(X) 具有常態分佈。這是對數常態分佈的 PDF：對數常態分佈的隨機變數只取正實數值。因此，對數常態分佈會建立右偏曲線。讓我們在 Python 中繪製它：

X = np.linspace(0, 6, 500) 
 
std = 1 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
 
fig, ax = plt.subplots(figsize=(8, 5)) 
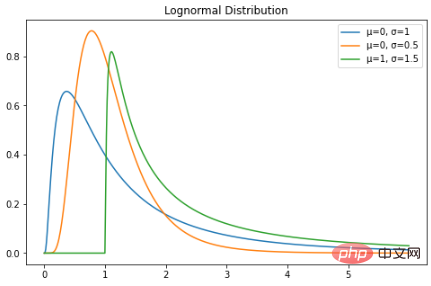
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=1") 
ax.set_xticks(np.arange(min(X), max(X))) 
 
std = 0.5 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=0.5") 
 
std = 1.5 
mean = 1 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=1, σ=1.5") 
 
plt.title("Lognormal Distribution") 
plt.legend() 
plt.show()

泊松分佈

泊松分佈以法國數學家西蒙·丹尼斯·泊鬆的名字命名。這是一個離散的機率分佈，這意味著它計算具有有限結果的事件——換句話說，它是一個計數分佈。因此，泊松分佈用於顯示事件在指定期間內可能發生的次數。如果一個事件在時間上以固定的速率發生，那麼及時觀察到事件的數量（n）的機率可以用泊松分佈來描述。例如，顧客可能以每分鐘 3 次的平均速度到達咖啡館。我們可以使用泊松分佈來計算 9 位客戶在 2 分鐘內到達的機率。下面是機率質量函數公式：λ 是一個時間單位的事件率——在我們的例子中，它是 3。 k 是出現的次數－在我們的例子中，它是 9。這裡可以使用 Scipy 來完成機率的計算。

from scipy import stats 

print(stats.poisson.pmf(k=9, mu=3))

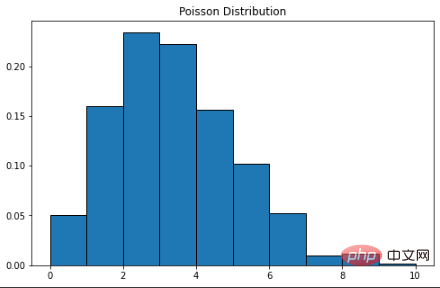
0.002700503931560479

泊松分佈的曲線類似常態分佈，λ 表示峰值。

X = stats.poisson.rvs(mu=3, size=500) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X, density=True, edgecolor="black") 
plt.title("Poisson Distribution") 
plt.show()

指數分佈

#

指数分布是泊松点过程中事件之间时间的概率分布。指数分布的概率密度函数如下：λ 是速率参数，x 是随机变量。

X = np.linspace(0, 5, 5000) 
 
exponetial_distribtuion = stats.expon.pdf(X, loc=0, scale=1) 
 
plt.subplots(figsize=(8,5)) 
plt.plot(X, exponetial_distribtuion) 
plt.title("Exponential Distribution") 
plt.show()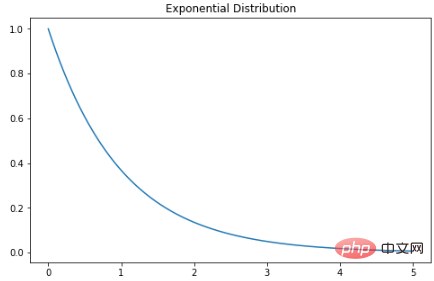

二项分布

可以将二项分布视为实验中成功或失败的概率。有些人也可能将其描述为抛硬币概率。参数为 n 和 p 的二项式分布是在 n 个独立实验序列中成功次数的离散概率分布，每个实验都问一个是 - 否问题，每个实验都有自己的布尔值结果：成功或失败。本质上，二项分布测量两个事件的概率。一个事件发生的概率为 p，另一事件发生的概率为 1-p。这是二项分布的公式：

• P = 二项分布概率
• = 组合数
• x = n次试验中特定结果的次数
• p = 单次实验中，成功的概率
• q = 单次实验中，失败的概率
• n = 实验的次数

可视化代码如下：

X = np.random.binomial(n=1, p=0.5, size=1000) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X) 
plt.title("Binomial Distribution") 
plt.show()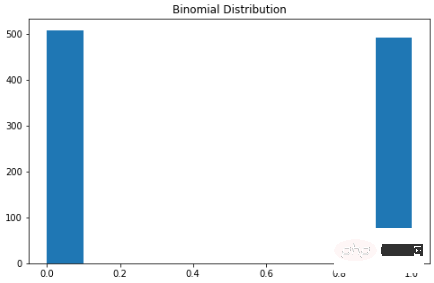

学生 t 分布

学生 t 分布（或简称 t 分布）是在样本量较小且总体标准差未知的情况下估计正态分布总体的均值时出现的连续概率分布族的任何成员。它是由英国统计学家威廉·西利·戈塞特（William Sealy Gosset）以笔名“student”开发的。PDF如下：n 是称为“自由度”的参数，有时可以看到它被称为“d.o.f.” 对于较高的 n 值，t 分布更接近正态分布。

import seaborn as sns 
from scipy import stats 
 
X1 = stats.t.rvs(df=1, size=4) 
X2 = stats.t.rvs(df=3, size=4) 
X3 = stats.t.rvs(df=9, size=4) 
 
plt.subplots(figsize=(8,5)) 
sns.kdeplot(X1, label = "1 d.o.f") 
sns.kdeplot(X2, label = "3 d.o.f") 
sns.kdeplot(X3, label = "6 d.o.f") 
plt.title("Student's t distribution") 
plt.legend() 
plt.show()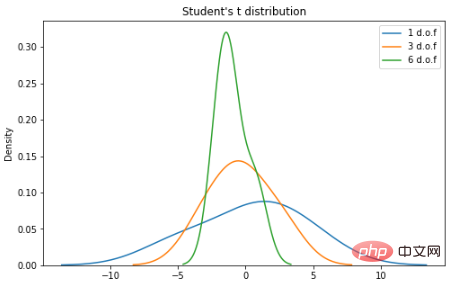

卡方分布

卡方分布是伽马分布的一个特例；对于 k 个自由度，卡方分布是一些独立的标准正态随机变量的 k 的平方和。PDF如下：这是一种流行的概率分布，常用于假设检验和置信区间的构建。在 Python 中绘制一些示例图：

X = np.arange(0, 6, 0.25) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=3), label="3 d.o.f") 
plt.title("Chi-squared Distribution") 
plt.legend() 
plt.show()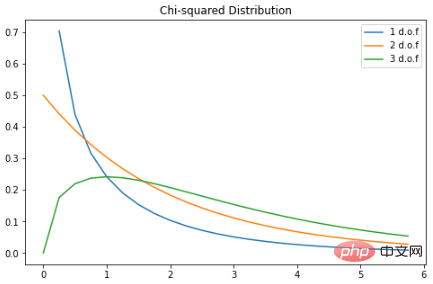

掌握统计学和概率对于数据科学至关重要。在本文展示了一些常见且常用的分布，希望对你有所帮助。

以上是Python實現八種機率分佈公式及資料視覺化教程的詳細內容。更多資訊請關注PHP中文網其他相關文章！