隨著深度學習模型的應用和推廣,人們逐漸發現模型常常會利用資料中存在的虛假關聯(Spurious Correlation)來獲得較高的訓練表現。但由於這類關聯在測驗資料上往往並不成立,因此這類模型的測驗表現往往不盡人意 [1]。其本質是由於傳統的機器學習目標(Empirical Risk Minimization,ERM)假設了訓練測試集的獨立同分佈特性,而在現實中該獨立同分佈假設成立的場景往往有限。在許多現實場景中,訓練資料的分佈與測試資料分佈通常表現出不一致性,即分佈偏移(Distribution Shifts),旨在提升模型在該類別場景下效能的問題通常被稱為分佈外泛化( Out-of-Distribution)問題。關注學習資料中的相關性而非因果性的 ERM 等一類方法往往難以應對分佈偏移。儘管近年來湧現了許多方法借助因果推論(Causal Inference)中的不變性原理(Invariance Principle)在分佈外泛化(Out-of-Distribution)問題上取得了一定的進展,但在圖數據上的研究依然有限。這是因為圖數據的分佈外泛化比傳統的歐式數據更困難,為圖機器學習帶來了更多的挑戰。本文以圖分類任務為例,對借助因果不變性原理的圖分佈外泛化進行了探究。

近年來,借助因果不變性原理,人們在歐式資料的分佈外泛化問題中取得了一定的成功,但對圖數據的研究仍然有限。與歐式資料不同,圖的複雜性對因果不變性原理的使用以及克服分佈外泛化難題提出了獨特的挑戰。
為了回應該挑戰,我們在本工作中將因果不變性融入圖機器學習中,並提出了因果啟發的不變圖學習框架,為解決圖資料的分佈外泛化問題提供了新的理論與方法。
論文已在 NeurIPS 2022 發表,本工作由香港中文大學、香港浸會大學, 騰訊 AI Lab 以及雪梨大學合作完成。

- 論文標題:Learning Causally Invariant Representations for Out-of-Distribution Generalization on Graphs
- #論文連結:https://openreview.net/forum?id=A6AFK_JwrIW
- 專案碼:https: //github.com/LFhase/CIGA
圖資料的分佈外泛化
圖資料的分佈外泛化難在哪?
圖神經網路近年來在涉及圖結構的機器學習應用,如推薦系統、AI 輔助製藥等領域,取得了巨大的成功。然而,由於現有的大部分的圖機器學習演算法都依賴資料的獨立同分佈假設,使得當測試資料和訓練資料出現偏移(Distribution Shifts)時,演算法的效能會極大下降。同時,因為圖資料結構的複雜性,導致圖資料的分佈外泛化相比於歐式資料更普遍且更具挑戰性。

圖 1. 圖上的分佈偏移範例。
首先,圖資料的分佈偏移可以出現在圖的節點特徵分佈中(Attribute-level Shifts)。例如,在推薦系統中,訓練資料涉及的商品可能採自一些比較流行的類別,涉及到的用戶也可能來自於某些特定地區,而在測試階段,系統則需要妥善處理所有類別以及地區的用戶和商品[2,3,4]。此外,圖資料的分佈偏移也可以出現在圖的結構分佈中(Structure-level Shifts)。早在2019 年,人們就注意到,在較小的圖上進行訓練得到的圖神經網路難以學到有效的注意力(Attention)權重以泛化到更大的圖上[5],這也推動了一系列相關工作的提出[6,7]。在現實場景中,這兩類分佈偏移往往可能同時出現,而這些不同層級的分佈偏移也可以和所要預測的標籤具有不同的虛假關聯模式。如在推薦系統中,來自特定類別的商品與特定地區的使用者往往會在商品使用者互動圖上展現獨特的拓樸結構 [4]。在藥物分子屬性預測中,訓練時涉及的藥物分子可能偏小,同時預測的結果也會受到實驗測定環境的影響 [8]。
此外,歐式空間的分佈外泛化往往會假設資料來自於多個環境(Environment)或領域(Domain),並進一步假設訓練期間模型能夠取得訓練資料中每個樣本所屬的環境,以此來發掘跨越環境的不變性。然而,要獲得數據的環境標籤往往需要和數據相關的一些專家知識,而由於圖數據的抽象性,使得圖數據的環境標籤獲得更加昂貴。因此,大部分現有的圖資料集如 OGB 都不含此類環境標籤訊息,即便少部分如 DrugOOD 資料集存在環境標籤,但也存在不同程度的雜訊。
現有方法能否解決圖上的分佈外泛化問題?
為了對圖資料分佈外泛化的挑戰有一個直觀的理解,我們基於Spurious-Motif [9] 資料集建構新的資料以進一步實例化上述幾大挑戰,並嘗試使用現有的方法如歐式數據上分佈外泛化的訓練目標IRM [10],或者俱有更強表達能力的GNN [11],分析能否透過已有的方法解決圖數據的分佈外泛化問題。

圖 2. Spurious Motif 資料集範例。
Spurious Motif 任務如圖2 所示,主要根據輸入的圖中是否含有特定結構的子圖(如House,或Cycle)對圖標籤進行判斷,其中節點顏色代表節點的屬性。使用此資料集可以比較清晰地測試不同層級的分佈偏移對圖神經網路效能的影響。對於一個使用ERM 進行訓練的普通GNN 模型:
- 如果訓練階段大部分有House 子圖的樣本都節點大部分綠色,而Cycle 則是藍色,那麼在測試階段,模型則傾向於預測任何含大量綠色節點的圖為“House”,而藍色節點的圖為“Cycle”。
- 如果訓練階段大部分有House 子圖的樣本都與一個六邊形子圖共同出現,那麼在測試階段,模型則傾向於判定任何含有六邊形結構的圖為「House」。
此外,模型在訓練時無法獲得任何和環境標籤相關的信息,得到實驗結果如圖 3 所示(更多結果可以查閱論文附錄 D)。

圖 3. 現有方法在不同圖分佈偏移下的表現。
如圖3 所示,普通的GCN 不論是在使用ERM 或IRM 訓練,都無法應對圖的結構偏移(Struc);而在增加了圖節點屬性偏移(Mixed)以及圖大小分佈偏移後(圖3 中),模型性能將進一步降低;此外即便使用具有更強表達能力的kGNN 也難以避免嚴重的性能損失(平均性能的降低,或更大的變異數)。
由此,我們自然引出所要研究的問題:如何才能得到一個具有應對多種圖分佈偏移的 GNN 模型?
主題分佈外泛化的因果模型
為了解決上述問題,我們需要對學習目標,即不變圖神經網路(Invariant GNN),進行定義,即在最糟糕的環境下仍舊表現良好的模型(嚴謹的定義參見論文):
定義1(不變圖神經網路)給定一系列收集自不同的具有因果關聯的環境的圖分類資料集#,其中包含被認為是來自環境e 的獨立同分佈樣本,考慮一個圖神經網路##和分別是作為輸入的圖空間和樣本空間,f 是不變圖神經網絡,當且僅當,即最小化所有環境的最壞經驗損失(worst empirical risk),其中為模型在環境中的經驗損失。
模型在訓練時只能獲得部分的訓練環境#中的數據,如果不對數據的過程進行任何假設,則不變圖神經網路定義所要求的minmax 最適性是很難做到的。因此,我們從因果推論(Causal Inference)的角度使用因果模型(Structural Causal Model)對圖的生成過程進行建模,並對環境之間的關聯進行刻畫,以嘗試定義圖資料上的因果不變性。

圖 4. 圖表資料產生過程的因果模型。
不失一般性,我們將所有影響圖產生的隱變數納入隱空間,並將圖的生成過程建模為 #。此外,對於隱變數
#。此外,對於隱變數 ,根據其是否受環境E 影響,我們將其劃分為不變性隱變數(invariant latent variable)
,根據其是否受環境E 影響,我們將其劃分為不變性隱變數(invariant latent variable) 以及虛假隱變量(spurious latent variable)
以及虛假隱變量(spurious latent variable) 。對應地,隱變數C 與S 分別會影響G 的某個子圖的生成,分別記作不變子圖
。對應地,隱變數C 與S 分別會影響G 的某個子圖的生成,分別記作不變子圖 以及假子圖
以及假子圖 ,如圖4 (a) 所示,而C 主要控制了圖的標籤Y。這也可以進一步推出
,如圖4 (a) 所示,而C 主要控制了圖的標籤Y。這也可以進一步推出 ,即 C 與 Y 相比於 S 有更高的互資訊。這樣的生成過程與許多實際例子相對應,如一個分子的藥化屬性通常由某個關鍵的基團(分子子圖)決定(如羥基 - HO 之於分子的水溶性)。
,即 C 與 Y 相比於 S 有更高的互資訊。這樣的生成過程與許多實際例子相對應,如一個分子的藥化屬性通常由某個關鍵的基團(分子子圖)決定(如羥基 - HO 之於分子的水溶性)。
此外,C 與Y,S以及E 在隱空間有多種類型的交互,主要跟進虛假隱變量S 與標籤Y 是否在有不變隱變量C 之外額外的關聯,即 ,可歸納為兩種:如圖4 (b) 的FIIF(Fully Informative Invariant Feature)以及圖4 (c) 的PIIF(Partially Informative Invariant Feature)。其中 FIIF 表示給定不變訊息後標籤與虛假相關量獨立。 PIIF 則相反。需要說明的是,為了盡可能地涵蓋更多的圖分佈偏移,我們的因果模型致力於對各種圖生成模型的廣泛的建模。如有更多關於圖生成過程的知識,圖 4 所示的因果模型則可以進一步泛化到更具體的例子。如在附錄 C.1 中,我們展示如何透過增加額外圖極限(graphon)的假設,將因果圖泛化至先前 Bevilacqua 等人用於分析圖大小分佈偏移的工作 [7]。
,可歸納為兩種:如圖4 (b) 的FIIF(Fully Informative Invariant Feature)以及圖4 (c) 的PIIF(Partially Informative Invariant Feature)。其中 FIIF 表示給定不變訊息後標籤與虛假相關量獨立。 PIIF 則相反。需要說明的是,為了盡可能地涵蓋更多的圖分佈偏移,我們的因果模型致力於對各種圖生成模型的廣泛的建模。如有更多關於圖生成過程的知識,圖 4 所示的因果模型則可以進一步泛化到更具體的例子。如在附錄 C.1 中,我們展示如何透過增加額外圖極限(graphon)的假設,將因果圖泛化至先前 Bevilacqua 等人用於分析圖大小分佈偏移的工作 [7]。
是基於上述的因果分析,我們可以知道,當模型只使用不變子圖來預測的時,也就是只使用 之間的關聯,模型的預測才不會受到環境E 的改變而影響;反之,如果模型的預測依賴於任何與S 或
之間的關聯,模型的預測才不會受到環境E 的改變而影響;反之,如果模型的預測依賴於任何與S 或 有關的信息,其預測結果將會因為E 的變化發生極大的改變,從而出現性能損失。因此,我們的目標可以從學習一個不變圖神經網絡,進一步細化至:a) 識別潛在的不變子圖;b) 用識別的子圖預測 Y。為了進一步與資料產生的演算法過程相對應,我們進一步將圖神經網路分割成子圖辨識網路(Featurizer GNN)
有關的信息,其預測結果將會因為E 的變化發生極大的改變,從而出現性能損失。因此,我們的目標可以從學習一個不變圖神經網絡,進一步細化至:a) 識別潛在的不變子圖;b) 用識別的子圖預測 Y。為了進一步與資料產生的演算法過程相對應,我們進一步將圖神經網路分割成子圖辨識網路(Featurizer GNN) 與分類網路(Classifier GNN)
與分類網路(Classifier GNN) #,且
#,且 ,其中
,其中 為
為 的子圖空間。那麼模型的學習目標則可表示為如公式 (1) 所示:
的子圖空間。那麼模型的學習目標則可表示為如公式 (1) 所示:

其中, ,為子圖辨識網路對不變子圖的預測;
,為子圖辨識網路對不變子圖的預測; ##為
##為







 ##與Y 的互訊息,通常,最大化
##與Y 的互訊息,通常,最大化 可以透過最小化使用
可以透過最小化使用 預測Y 的經驗損失實現。然而,由於E 的缺失,我們難以直接使用E 對
預測Y 的經驗損失實現。然而,由於E 的缺失,我們難以直接使用E 對
進行獨立性 的驗證,為此,我們必須尋求其他等價條件以識別需要的不變子圖。
的驗證,為此,我們必須尋求其他等價條件以識別需要的不變子圖。  因果啟發的不變圖學習
因果啟發的不變圖學習
- 不同環境,中與相同不變隱變數C 的不變子圖是這兩個環境中互資訊最大的兩個子圖,即;

中對應不同不變隱變數C 的不變子圖兩個不變子圖就是這個環境中互資訊最小的兩個子圖,即
 ;
; ##結合上述兩個性質,我們可以推出
##結合上述兩個性質,我們可以推出

由於在實務上我們難以直接觀察得到,我們則可以透過公式(2) 中的代理人使用。 
 同時,當
同時,當 和
和
注意到,在最大化時, 可能會出現
可能會出現


 ##中的假子圖部分與被移除的不變子圖部分享有同樣的和相關的互資訊。那麼,我們能否反其道而行之,同時最大化
##中的假子圖部分與被移除的不變子圖部分享有同樣的和相關的互資訊。那麼,我們能否反其道而行之,同時最大化 以去除
以去除 中可能的假子圖部分呢?答案是肯定的,我們可以利用
中可能的假子圖部分呢?答案是肯定的,我們可以利用 與 Y 的關聯令其與
與 Y 的關聯令其與 的估計互相競爭。需要注意的是,在最大化
的估計互相競爭。需要注意的是,在最大化 時需要保證
時需要保證
不會超過
又將陷入平凡解。結合這額外的條件,我們可以將關於不變子圖大小的假設從公式(3) 移除,得到如下CIGAv2:
圖5. 因果啟發的不變圖學習框架示意圖。 
其中 對應著公式(4) 中的正樣本,而
對應著公式(4) 中的正樣本,而 則對應於
則對應於 的圖表示。當
的圖表示。當 時,公式(5) 提供了對於
時,公式(5) 提供了對於 的一種基於von Mises-Fisher kernel density 的非參數再代入熵估計(Nonparameteric Resubstitution Entropy Estimator )[13,14]。最終CIGA 核心部分的實現如圖5 所示,即透過在隱表示空間拉近同個類別不變子圖的圖表示,同時最大化不同類別不變子圖的圖表示,以最大化
的一種基於von Mises-Fisher kernel density 的非參數再代入熵估計(Nonparameteric Resubstitution Entropy Estimator )[13,14]。最終CIGA 核心部分的實現如圖5 所示,即透過在隱表示空間拉近同個類別不變子圖的圖表示,同時最大化不同類別不變子圖的圖表示,以最大化  。此外,對於公式(4) 中的另一個約束,我們則可以透過鉸鏈損失(hinge loss)的思路進行實現,即
。此外,對於公式(4) 中的另一個約束,我們則可以透過鉸鏈損失(hinge loss)的思路進行實現,即 ,只優化預測時經驗損失大於對應的不變子圖的虛假子圖。
,只優化預測時經驗損失大於對應的不變子圖的虛假子圖。
實驗與討論
在實驗中,我們使用16 個合成或來自真實世界的資料集,對CIGA 在不同圖分佈偏移下進行了充分的驗證。在實驗中,我們使用可解釋 GNN 框架 [9] 實現了 CIGA 的原型,而實際上 CIGA 有更多實現的方式。具體的資料集以及實驗細節詳見文中實驗部分。
合成資料集上圖結構分佈偏移以及混合分佈偏移的表現
我們首先基於SPMotif資料集[9] 建構了SPMotif-Struc 以及SPMotif-Mixed 資料集,其中SPMotif-Struc 包含了特定子圖與圖中其他子圖結構的虛假關聯,以及圖大小的分佈偏移;而SPMotif-Mixed 則在SPMotif-Struc 的基礎上新增了圖節點屬性層級的分佈偏移。表中第一欄為 ERM 以及可解釋 GNN 的基線,第二欄則為歐式空間最先進的分佈外泛化演算法。從結果可以發現,不論是更好的GNN 框架還是歐式空間的分佈外泛化演算法,都受制於圖上的分佈偏移,且當更多的分佈偏移出現時,性能損失(更小的平均分類性能或更大的變異數)將進一步增強。相對的,CIGA 則能在不同強度的分佈偏移下保持良好的性能,並極大超越最好的基線表現。

#真實資料集上各類別圖分佈偏移的表現
### #我們接著在真實資料集和各種真實資料中存在的圖分佈偏移進一步測試了CIGA 的表現,包括來自AI 輔助製藥中藥物分子屬性預測的DrugOOD 中三種不同環境劃分(實驗環境Assay,分子骨架Scaffold,分子大小Size)的三個資料集,包含了各種真實應用場景的圖分佈偏移;基於歐式空間中經典的影像資料集ColoredMNIST [10] 轉換得到的CMNIST-SP,主要包含圖節點屬性的PIIF 類型分佈偏移;基於自然語言情感分類資料集SST5 以及Twitter 轉換得到的Graph-SST5 以及Twitter [15],並且額外添加了圖度數的分佈偏移。此外,我們也使用了先前研究較多的 4 個分子圖大小分佈偏移資料集 [7],######


測試結果如上表所示,可以發現,在真實資料中,由於任務難度增加,使用更好架構的GNN或歐式空間的分佈外泛化最佳化目標訓練所得到的模型表現甚至比使用ERM 訓練所得到的普通GNN 模型還弱。這現像也與歐式空間中較難任務下的分佈外泛化實驗觀察得到的現象類似 [16],反應了真實資料上的分佈外泛化難度以及現有方法的不足。與之相對地,CIGA 則能在所有的真實資料和圖分佈偏移上獲得提升,甚至在某些資料集如 Twitter、PROTEINS 中達到經驗最優的 Oracle 水準。在最新的圖分佈外泛化測試基準 GOOD 上圖分類資料集的初步測試也顯示了 CIGA 是目前最好且能應對各種各樣的圖分佈偏移的圖分佈外泛化演算法。
由於使用了可解釋GNN 作為CIGA 的原型實現架構,我們也對模型識別得到的DrugOOD 中的進行了可視化,發現CIGA 確實發現了一些比較一致的分子基團用於分子屬性預測。這可以為後續 AI 輔助製藥提供更好的依據。

圖 6. DrugOOD 中 CIGA 辨識得到的部分不變子圖。
總結及展望
本文透過因果推論的角度,首次將因果不變性引入至多種圖分佈偏移下的圖分佈在外泛化問題中,並提出了一個全新的具有理論保證的解決架構CIGA。大量實驗也充分驗證了 CIGA 優秀的分佈外泛化效能。放眼未來,基於CIGA,我們可以進一步探索更好的實現框架[17],或為CIGA 引入更好的具有理論保障的資料增強方法[3,18],並在理論上建模納入圖上的協變數偏移(Covariate Shift)[19],以進一步提升CIGA 辨識不變子圖的能力,促進圖神經網路在AI 輔助製藥等真實應用情境的真實落地使用。
以上是港中文等提出的因果表示學習方法針對複雜直面圖資料分佈的外泛化問題的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 AI技能差距正在減慢供應鏈Apr 26, 2025 am 11:13 AM
AI技能差距正在減慢供應鏈Apr 26, 2025 am 11:13 AM經常使用“ AI-Ready勞動力”一詞,但是在供應鏈行業中確實意味著什麼? 供應鏈管理協會(ASCM)首席執行官安倍·埃什肯納齊(Abe Eshkenazi)表示,它表示能夠評論家的專業人員
 一家公司如何悄悄地努力改變AIApr 26, 2025 am 11:12 AM
一家公司如何悄悄地努力改變AIApr 26, 2025 am 11:12 AM分散的AI革命正在悄悄地獲得動力。 本週五在德克薩斯州奧斯汀,Bittensor最終遊戲峰會標誌著一個關鍵時刻,將分散的AI(DEAI)從理論轉變為實際應用。 與閃閃發光的廣告不同
 NVIDIA釋放NEMO微服務以簡化AI代理開發Apr 26, 2025 am 11:11 AM
NVIDIA釋放NEMO微服務以簡化AI代理開發Apr 26, 2025 am 11:11 AM企業AI面臨數據集成挑戰 企業AI的應用面臨一項重大挑戰:構建能夠通過持續學習業務數據來保持準確性和實用性的系統。 NeMo微服務通過創建Nvidia所描述的“數據飛輪”來解決這個問題,允許AI系統通過持續接觸企業信息和用戶互動來保持相關性。 這個新推出的工具包包含五個關鍵微服務: NeMo Customizer 處理大型語言模型的微調,具有更高的訓練吞吐量。 NeMo Evaluator 提供針對自定義基準的AI模型簡化評估。 NeMo Guardrails 實施安全控制,以保持合規性和適當的
 AI為藝術與設計的未來描繪了一幅新圖片Apr 26, 2025 am 11:10 AM
AI為藝術與設計的未來描繪了一幅新圖片Apr 26, 2025 am 11:10 AMAI:藝術與設計的未來畫卷 人工智能(AI)正以前所未有的方式改變藝術與設計領域,其影響已不僅限於業餘愛好者,更深刻地波及專業人士。 AI生成的藝術作品和設計方案正在迅速取代傳統的素材圖片和許多交易性設計活動中的設計師,例如廣告、社交媒體圖片生成和網頁設計。 然而,專業藝術家和設計師也發現AI的實用價值。他們將AI作為輔助工具,探索新的美學可能性,融合不同的風格,創造新穎的視覺效果。 AI幫助藝術家和設計師自動化重複性任務,提出不同的設計元素並提供創意輸入。 AI支持風格遷移,即將一種圖像的風格應用
 Zoom如何徹底改變與Agent AI的合作:從會議到里程碑Apr 26, 2025 am 11:09 AM
Zoom如何徹底改變與Agent AI的合作:從會議到里程碑Apr 26, 2025 am 11:09 AMZoom最初以其視頻會議平台而聞名,它通過創新使用Agentic AI來引領工作場所革命。 最近與Zoom的CTO XD黃的對話揭示了該公司雄心勃勃的願景。 定義代理AI 黃d
 對大學的存在威脅Apr 26, 2025 am 11:08 AM
對大學的存在威脅Apr 26, 2025 am 11:08 AMAI會徹底改變教育嗎? 這個問題是促使教育者和利益相關者的認真反思。 AI融入教育既提出了機遇和挑戰。 正如科技Edvocate的馬修·林奇(Matthew Lynch)所指出的那樣
 原型:美國科學家正在國外尋找工作Apr 26, 2025 am 11:07 AM
原型:美國科學家正在國外尋找工作Apr 26, 2025 am 11:07 AM美國科學研究和技術發展或將面臨挑戰,這或許是由於預算削減導致的。據《自然》雜誌報導,2025年1月至3月期間,美國科學家申請海外工作的數量比2024年同期增加了32%。此前一項民意調查顯示,75%的受訪研究人員正在考慮前往歐洲和加拿大尋找工作。 過去幾個月,數百項NIH和NSF的撥款被終止,NIH今年的新撥款減少了約23億美元,下降幅度接近三分之一。洩露的預算提案顯示,特朗普政府正在考慮大幅削減科學機構的預算,削減幅度可能高達50%。 基礎研究領域的動盪也影響了美國的一大優勢:吸引海外人才。 35
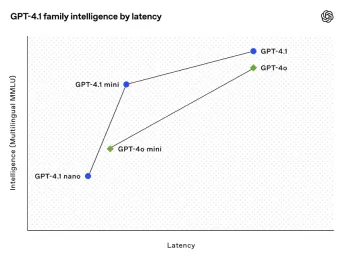 所有有關打開AI最新的GPT 4.1家庭的信息 - 分析VidhyaApr 26, 2025 am 10:19 AM
所有有關打開AI最新的GPT 4.1家庭的信息 - 分析VidhyaApr 26, 2025 am 10:19 AMOpenai推出了強大的GPT-4.1系列:一個專為現實世界應用設計的三種高級語言模型家族。 這種巨大的飛躍提供了更快的響應時間,增強的理解和大幅降低了成本


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

EditPlus 中文破解版
體積小,語法高亮,不支援程式碼提示功能

Atom編輯器mac版下載
最受歡迎的的開源編輯器

MinGW - Minimalist GNU for Windows
這個專案正在遷移到osdn.net/projects/mingw的過程中,你可以繼續在那裡關注我們。 MinGW:GNU編譯器集合(GCC)的本機Windows移植版本,可自由分發的導入函式庫和用於建置本機Windows應用程式的頭檔;包括對MSVC執行時間的擴展,以支援C99功能。 MinGW的所有軟體都可以在64位元Windows平台上運作。

Dreamweaver CS6
視覺化網頁開發工具

SecLists
SecLists是最終安全測試人員的伙伴。它是一個包含各種類型清單的集合,這些清單在安全評估過程中經常使用,而且都在一個地方。 SecLists透過方便地提供安全測試人員可能需要的所有列表,幫助提高安全測試的效率和生產力。清單類型包括使用者名稱、密碼、URL、模糊測試有效載荷、敏感資料模式、Web shell等等。測試人員只需將此儲存庫拉到新的測試機上,他就可以存取所需的每種類型的清單。






