Java二元搜尋樹的增、插、刪和創建範例詳解

①概念

二元搜尋樹又稱為二元排序樹，它或是一棵空樹**，或是具有以下性質的二元樹:

若它的左子樹不為空，則左子樹上所有節點的值都小於根節點的值

若它的右子樹不為空，則右子樹上所有節點的值都大於根節點的值

它的左右子樹也分別為二元搜尋樹

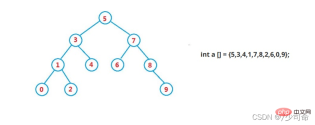
②運算-尋找

二元搜尋樹的查找類似於二分法查找

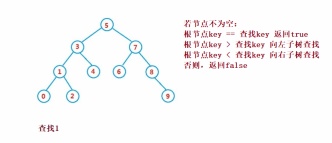
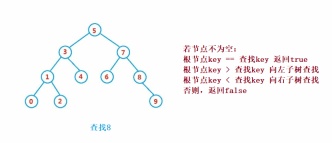
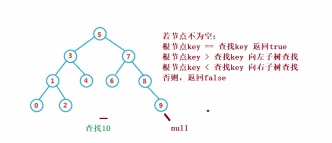
public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(cur.val < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }

③操作-插入

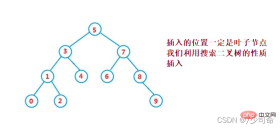
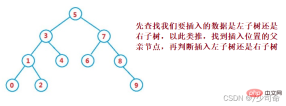
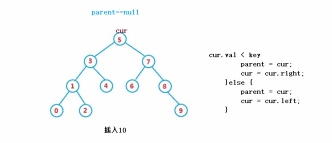
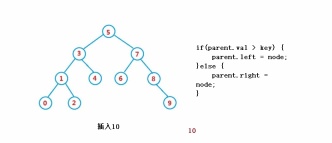
  public boolean insert(int key) {
        Node node = new Node(key);
        if(root == null) {
            root = node;
            return true;
        }
 
        Node cur = root;
        Node parent = null;
 
        while(cur != null) {
            if(cur.val == key) {
                return false;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //parent
        if(parent.val > key) {
            parent.left = node;
        }else {
            parent.right = node;
        }
 
        return true;
    }

④操作-刪除

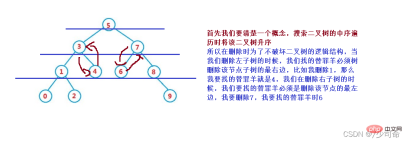
刪除操作較為複雜，但理解了其原理還是比較容易

設待刪除結點為cur, 待刪除結點的雙親結點為parent

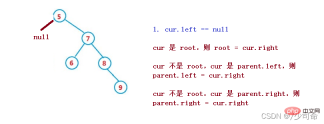
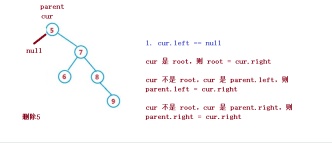
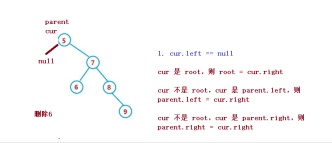
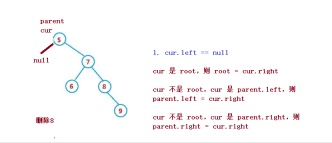
1. cur.left == null

1. cur 是root，則root = cur.right

2. cur 不是root，cur 是parent.left，則parent.left = cur.right

3. cur 不是root，cur 是parent.right，則parent.right = cur.right

##2. cur.right == null

1. cur 是root，則root = cur.left

2. cur 不是root，cur 是parent.left，則parent.left = cur.left

3. cur 不是root，cur 是parent.right，則parent.right = cur.left

第二種情況和第一種情況相同，只是方向相反，這裡不再畫圖

3. cur.left != null && cur.right != null

#需要使用替換法進行刪除，即在它的右子樹中尋找中序下的第一個結點(關鍵碼最小)，用它的值填補到被刪除節點中，再來處理該結點的刪除問題

當我們在左右子樹都不為空的情況下進行刪除，刪除該節點會破壞樹的結構，因此用替罪羊的方法來解決，實際刪除的過程還是上面的兩種情況，這裡還是用到了搜尋二元樹的性質

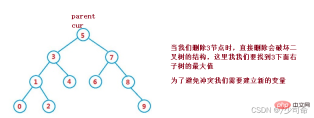
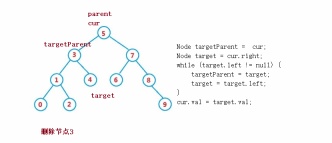
public void remove(Node parent,Node cur) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node targetParent =  cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
 
  public void removeKey(int key) {
        if(root == null) {
            return;
        }
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                remove(parent,cur);
                return;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }

⑤效能分析

插入和刪除操作都必須先查找，查找效率代表了二元搜尋樹中各個操作的效能。

對有n個結點的二元搜尋樹，若每個元素尋找的機率相等，則二元搜尋樹平均找出長度是結點在二元搜尋樹的深度的函數，即結點越深，則比較次數越多。

但對於同一個關鍵碼集合，如果各關鍵碼插入的次序不同，可能會得到不同結構的二元搜尋樹：

最優情況下，二元搜尋樹為完全二元樹，其平均比較次數為：

最差情況下，二元搜尋樹退化為單支樹，其平均比較次數為：

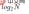
⑥完整代码

public class TextDemo {
 
    public static class Node {
        public int val;
        public Node left;
        public Node right;
 
        public Node (int val) {
            this.val = val;
        }
    }
 
 
    public Node root;
 
    /**
     * 查找
     * @param key
     */
    public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(cur.val < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }
 
    /**
     *
     * @param key
     * @return
     */
    public boolean insert(int key) {
        Node node = new Node(key);
        if(root == null) {
            root = node;
            return true;
        }
 
        Node cur = root;
        Node parent = null;
 
        while(cur != null) {
            if(cur.val == key) {
                return false;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //parent
        if(parent.val > key) {
            parent.left = node;
        }else {
            parent.right = node;
        }
 
        return true;
    }
 
    public void remove(Node parent,Node cur) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node targetParent =  cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
 
    public void removeKey(int key) {
        if(root == null) {
            return;
        }
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                remove(parent,cur);
                return;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }
 
}

以上是Java二元搜尋樹的增、插、刪和創建範例詳解的詳細內容。更多資訊請關注PHP中文網其他相關文章！