Java中如何使用堆疊來解決Top-k問題？

1、什麼是堆？

堆疊結構

堆其實就是一種二元樹，但是普通的二元樹是以鍊式結構進行儲存資料的，而堆是以數組進行順序儲存資料的。那麼什麼樣的二元樹才適合用順序儲存的方式呢？

我們假設一顆普通的二元樹可以用數組存儲，那麼就可以得到如下結構：

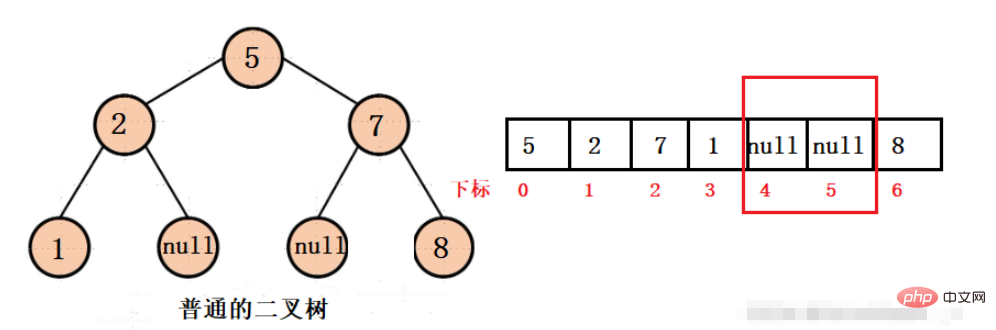
我們可以看到，當二元樹中間有空值時，數組的儲存空間會被浪費，那麼什麼情況下空間才不會被浪費呢？那就是完全二元樹。

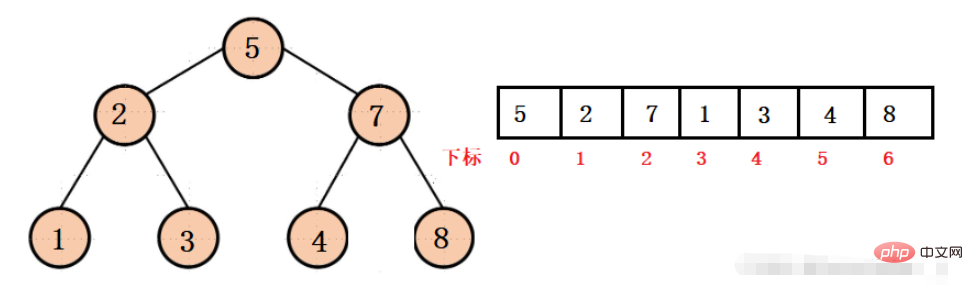
從以上結構中，我們不能用鍊式結構的指標來存取孩子節點或父親節點，只能透過對應下標來訪問，其實也比較簡單。

例如下圖：

知道2 節點的下標是1，那麼

他的左孩子下標是：2 * 2 1 = 3

他的右孩子下標是：2 * 2 2 = 4

相反，已知1 節點的下標是3，3 節點的下標是4，那麼

1 節點的父親節點下標是：(3 - 1) / 2 = 1

3 節點的父親節點下標是：(4 - 1) / 2 = 1

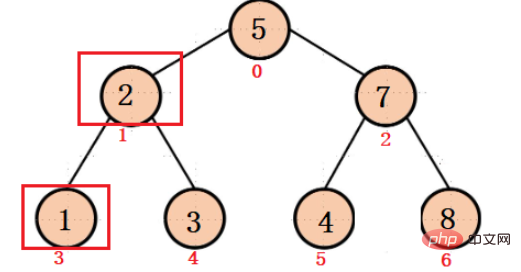
#大根堆VS 小根堆

大根堆（最大堆）

大根堆保證，每顆二叉樹的根節點都大於左右孩子節點

從最後一棵子樹的根節點開始調整，來到每顆子樹的根節點，使得每棵子樹都向下調整為大根堆，最後再向下做最後調整，保證二叉樹整體是大根堆（這個調整主要是為了後面的堆排序）。

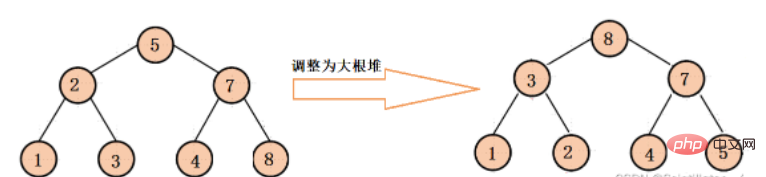
具體調整過程如下：

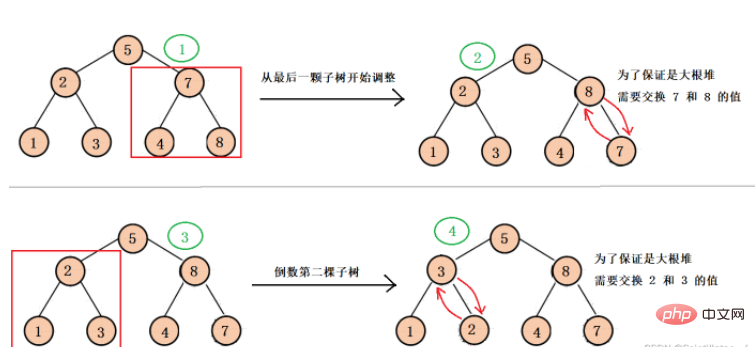
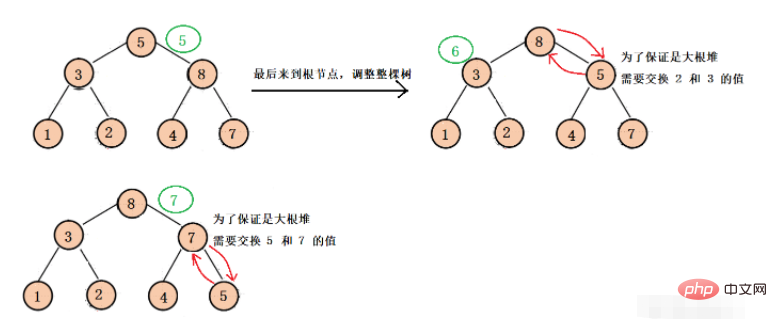
怎麼用程式碼實作呢？

我們先從最後一棵子樹調整，那麼就要拿到最後一顆子樹的根節點parent ，我們知道數組最後一個節點下標是len - 1，而這個節點是最後一棵子樹的左孩子或右孩子，根據孩子下標就可以拿到根節點下標( parent ) ，parent-- 就可以讓每顆子樹都進行調整，直到來到根節點，再向下調整最後一次，便可以得到大根堆。

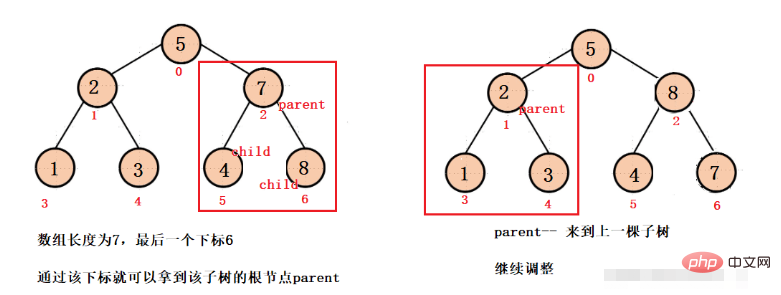
// 将数组变成大根堆结构
public void createHeap(int[] arr){
    for (int i = 0; i < arr.length; i++) {
        elem[i] = arr[i];// 放入elem[],假设不需要扩容
        usedSize++;
    }
    // 得到根节点parent, parent--依次来到每颗子树的根节点，
    for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {
        // 依次向下搜索，使得每颗子树都变成大根堆
        shiftDown(parent,usedSize);
    }
}
// 向下搜索变成大根堆
public void shiftDown(int parent,int len){
    int child = parent*2+1;// 拿到左孩子
    while (child < len){
        // 如果有右孩子,比较左右孩子大小,得到较大的值和父节点比较 
        if (child+1 < len && (elem[child] < elem[child+1])){
            child++;
        }
        // 比较较大的孩子和父节点,看是否要交换
        int max = elem[parent] >= elem[child] ? parent : child;
        if (max == parent) break;// 如果不需要调整了，说明当前子树已经是大根堆了，直接 break
        swap(elem,parent,child);
        parent = child;// 继续向下检测，看是否要调整
        child = parent*2+1;
    }
}
public void swap(int[] arr,int i,int j){
  	int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

小根堆（最小堆）

小根堆保證，每顆二元樹的根節點都小於左右孩子節點

調整過程同上。

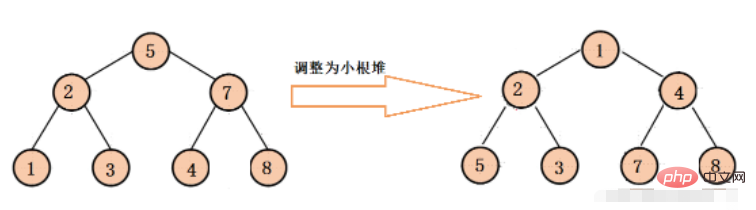
優先權佇列（PriorityQueue）

#在java中，提供了堆這種資料結構（PriorityQueue），也叫優先權佇列，當我們創建一個這樣的物件時，就得到了一個沒有添加資料的小根堆，我們可以向裡面添加或刪除元素，每向裡面刪除或添加一個元素，系統會整體進行一次調整，重新調整為小根堆。

// 默认得到一个小根堆
PriorityQueue<Integer> smallHeap = new PriorityQueue<>();
smallHeap.offer(23);
smallHeap.offer(2);
smallHeap.offer(11);
System.out.println(smallHeap.poll());// 弹出2，剩余最小的元素就是11，会被调整到堆顶，下一次弹出
System.out.println(smallHeap.poll());// 弹出11

 // 如果需要得到大根堆，在里面传一个比较器
 PriorityQueue<Integer> BigHeap = new PriorityQueue<>(new Comparator<Integer>() {
     @Override
     public int compare(Integer o1, Integer o2) {
         return o2 - o1;
     }
 });

2、top-k問題解決想法

#例：有一堆元素，讓你找出前三個最小的元素。

思路一： 將陣列從小到大排序，拿到陣列前3個元素。但可以發現這樣時間複雜度太高，不可取。

想法二： 將元素全部放入一個堆結構中，然後彈出三個元素，每次彈出的元素都是當前堆最小的，那麼彈出的三個元素就是前最小的三個元素。

這種思路可以做，但是假設我有1000000個元素，只彈出前三個最小的元素，那麼就要用到大小為1000000的堆。這麼做空間複雜度太高，不建議用這種方法。

思路三：

我們需要得到三個最小的元素，那就建一個大小為3的堆，假設目前的堆結構中剛好放滿了3個元素，那麼這三個元素就是目前最小的三個元素。假設第四個元素是我們想要的元素之一，那麼前三個至少有一個元素不是我們想要的，就需要彈出，那麼彈出誰呢？

我們要得到的是前三個最小的元素，所以目前堆結構中最大的元素一定不是我們想要的，所以這裡我們建造一個大根堆。彈出該元素，然後放入第四個元素，直到遍歷完整個陣列。

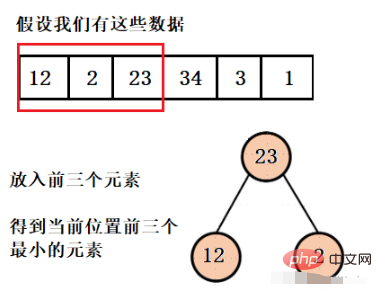
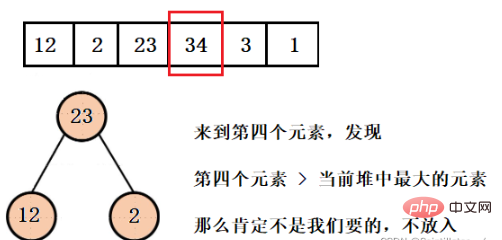
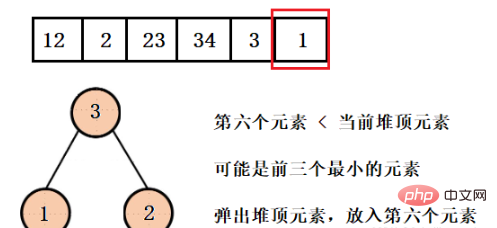
这样我们就得到了只含有前三个最小元素的堆，并且可以看到堆的大小一直都是3，而不是有多少数据就建多大的堆，然后再依次弹出元素就行了。

// 找前 k个最小的元素
public static int[] topK(int[] arr,int k){
     // 创建一个大小为 k的大根堆
     PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k,new Comparator<Integer>() {
         @Override
         public int compare(Integer o1, Integer o2) {
             return o2 - o1;
         }
     });
     for (int i = 0; i < arr.length; i++) {
         if (i < k){
             // 放入前 k 个元素
             maxHeap.offer(arr[i]);
         }else{
             // 从第 k+1个元素开始进行判断是否要入堆
             if (maxHeap.peek() > arr[i]){
                 maxHeap.poll();
                 maxHeap.offer(arr[i]);
             }
         }
     }
     int[] ret = new int[k];
     for (int i = 0; i < k; i++) {
         ret[i] = maxHeap.poll();
     }
     return ret;
 }

以上是Java中如何使用堆疊來解決Top-k問題？的詳細內容。更多資訊請關注PHP中文網其他相關文章！