如何使用Python實現遺傳演算法

遺傳演算法是模仿自然界生物演化機制發展出來的隨機全局搜尋和最佳化方法，它藉鑒了達爾文的進化論和孟德爾的遺傳學說。其本質是一種高效、平行、全局搜尋的方法，它能在搜尋過程中自動獲取和累積有關搜尋空間的知識，並自適應的控制搜尋過程以求得最優解。遺傳演算法操作使用適者生存的原則，在潛在的解決方案族群中逐次產生一個近似最優解的方案，在遺傳演算法的每一代中，根據個體在問題域中的適應度值和從自然遺傳學中藉鏡的再造方法進行個體選擇，產生一個新的近似解。這個過程導致族群中個體的演化，所得到的新個體比原來個體更能適應環境，就像自然界中的改造。

遺傳演算法具體步驟：

（1）初始化：設定演化代數計數器t=0、設定最大演化代數T、交叉機率、變異機率、隨機產生M 個個體作為初始族群P

（2）個體評估：計算族群P 中各個個體的適應度

（3）選擇運算：將選擇算子作用於群體。以個體適應度為基礎，選擇最優個體直接遺傳到下一代或透過配對交叉產生新的個體再遺傳到下一代

（4）交叉運算：在交叉機率的控制下，對群體中的個體兩兩進行交叉

（5）變異運算：在變異機率的控制下，對群體中的個體進行變異，即對某一個體的基因進行隨機調整

（6） 經過選擇、交叉、變異運算之後得到下一代群體P1。

重複以上（1）-（6），直到遺傳代數為 T，以進化過程中所得到的具有最優適應度個體作為最優解輸出，終止計算。

旅行推銷員問題（Travelling Salesman Problem， TSP）：有n 個城市，一個推銷員要從其中某一個城市出發，唯一走遍所有的城市，再回到他出發的城市，求最短的路線。

應用遺傳演算法求解 TSP 問題時需要進行一些約定，基因是一組城市序列，適應度是依照這個基因的城市順序的距離和分之一。

1.2 實驗代碼

import random
import math
import matplotlib.pyplot as plt
# 读取数据
f=open("test.txt")
data=f.readlines()
# 将cities初始化为字典，防止下面被当成列表
cities={}
for line in data:
    #原始数据以\n换行，将其替换掉
    line=line.replace("\n","")
    #最后一行以EOF为标志，如果读到就证明读完了，退出循环
    if(line=="EOF"):
        break
    #空格分割城市编号和城市的坐标
    city=line.split(" ")
    map(int,city)
    #将城市数据添加到cities中
    cities[eval(city[0])]=[eval(city[1]),eval(city[2])]
 
# 计算适应度，也就是距离分之一，这里用伪欧氏距离
def calcfit(gene):
    sum=0
    #最后要回到初始城市所以从-1，也就是最后一个城市绕一圈到最后一个城市
    for i in range(-1,len(gene)-1):
        nowcity=gene[i]
        nextcity=gene[i+1]
        nowloc=cities[nowcity]
        nextloc=cities[nextcity]
        sum+=math.sqrt(((nowloc[0]-nextloc[0])**2+(nowloc[1]-nextloc[1])**2)/10)
 
    return 1/sum
 
# 每个个体的类，方便根据基因计算适应度
class Person:
    def __init__(self,gene):
        self.gene=gene
        self.fit=calcfit(gene)
class Group:
    def __init__(self):
        self.GroupSize=100  #种群规模
        self.GeneSize=48    #基因数量，也就是城市数量
        self.initGroup()
        self.upDate()
    #初始化种群，随机生成若干个体
    def initGroup(self):
        self.group=[]
        i=0
        while(i<self.GroupSize):
            i+=1
            #gene如果在for以外生成只会shuffle一次
            gene=[i+1 for i in range(self.GeneSize)]
            random.shuffle(gene)
            tmpPerson=Person(gene)
            self.group.append(tmpPerson)
 
    #获取种群中适应度最高的个体
    def getBest(self):
        bestFit=self.group[0].fit
        best=self.group[0]
        for person in self.group:
            if(person.fit>bestFit):
                bestFit=person.fit
                best=person
        return best
    #计算种群中所有个体的平均距离
    def getAvg(self):
        sum=0
        for p in self.group:
            sum+=1/p.fit
        return sum/len(self.group)
    #根据适应度，使用轮盘赌返回一个个体，用于遗传交叉
    def getOne(self):
        #section的简称，区间
        sec=[0]
        sumsec=0
        for person in self.group:
            sumsec+=person.fit
            sec.append(sumsec)
        p=random.random()*sumsec
        for i in range(len(sec)):
            if(p>sec[i] and p<sec[i+1]):
                #这里注意区间是比个体多一个0的
                return self.group[i]
    #更新种群相关信息
    def upDate(self):
        self.best=self.getBest()
# 遗传算法的类，定义了遗传、交叉、变异等操作
class GA:
    def __init__(self):
        self.group=Group()
        self.pCross=0.35    #交叉率
        self.pChange=0.1    #变异率
        self.Gen=1  #代数
 
    #变异操作
    def change(self,gene):
        #把列表随机的一段取出然后再随机插入某个位置
        #length是取出基因的长度，postake是取出的位置，posins是插入的位置
        geneLenght=len(gene)
        index1 = random.randint(0, geneLenght - 1)
        index2 = random.randint(0, geneLenght - 1)
        newGene = gene[:]       # 产生一个新的基因序列，以免变异的时候影响父种群
        newGene[index1], newGene[index2] = newGene[index2], newGene[index1]
        return newGene
 
    #交叉操作
    def cross(self,p1,p2):
        geneLenght=len(p1.gene)
        index1 = random.randint(0, geneLenght - 1)
        index2 = random.randint(index1, geneLenght - 1)
        tempGene = p2.gene[index1:index2]   # 交叉的基因片段
        newGene = []
        p1len = 0
        for g in p1.gene:
              if p1len == index1:
                    newGene.extend(tempGene)     # 插入基因片段
                    p1len += 1
              if g not in tempGene:
                    newGene.append(g)
                    p1len += 1
        return newGene
 
    #获取下一代
    def nextGen(self):
        self.Gen+=1
        #nextGen代表下一代的所有基因
        nextGen=[]
        #将最优秀的基因直接传递给下一代
        nextGen.append(self.group.getBest().gene[:])
        while(len(nextGen)<self.group.GroupSize):
            pChange=random.random()
            pCross=random.random()
            p1=self.group.getOne()
            if(pCross<self.pCross):
                p2=self.group.getOne()
                newGene=self.cross(p1,p2)
            else:
                newGene=p1.gene[:]
            if(pChange<self.pChange):
                newGene=self.change(newGene)
            nextGen.append(newGene)
        self.group.group=[]
        for gene in nextGen:
            self.group.group.append(Person(gene))
            self.group.upDate()
 
    #打印当前种群的最优个体信息
    def showBest(self):
        print("第{}代\t当前最优{}\t当前平均{}\t".format(self.Gen,1/self.group.getBest().fit,self.group.getAvg()))
 
    #n代表代数，遗传算法的入口
    def run(self,n):
        Gen=[]  #代数
        dist=[] #每一代的最优距离
        avgDist=[]  #每一代的平均距离
        #上面三个列表是为了画图
        i=1
        while(i<n):
            self.nextGen()
            self.showBest()
            i+=1
            Gen.append(i)
            dist.append(1/self.group.getBest().fit)
            avgDist.append(self.group.getAvg())
        #绘制进化曲线
        plt.plot(Gen,dist,&#39;-r&#39;)
        plt.plot(Gen,avgDist,&#39;-b&#39;)
        plt.show()
 
ga=GA()
ga.run(3000)
print("进行3000代后最优解：",1/ga.group.getBest().fit)

1.3 實驗結果

下圖是進行一次實驗的結果截圖，求出的最優解是11271

為避免實驗的偶然性，進行10 次重複實驗，並求平均值，結果如下。

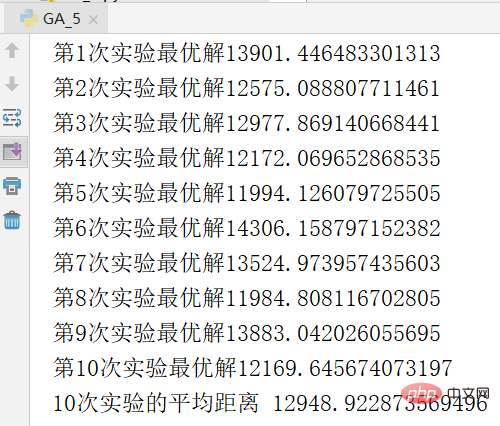
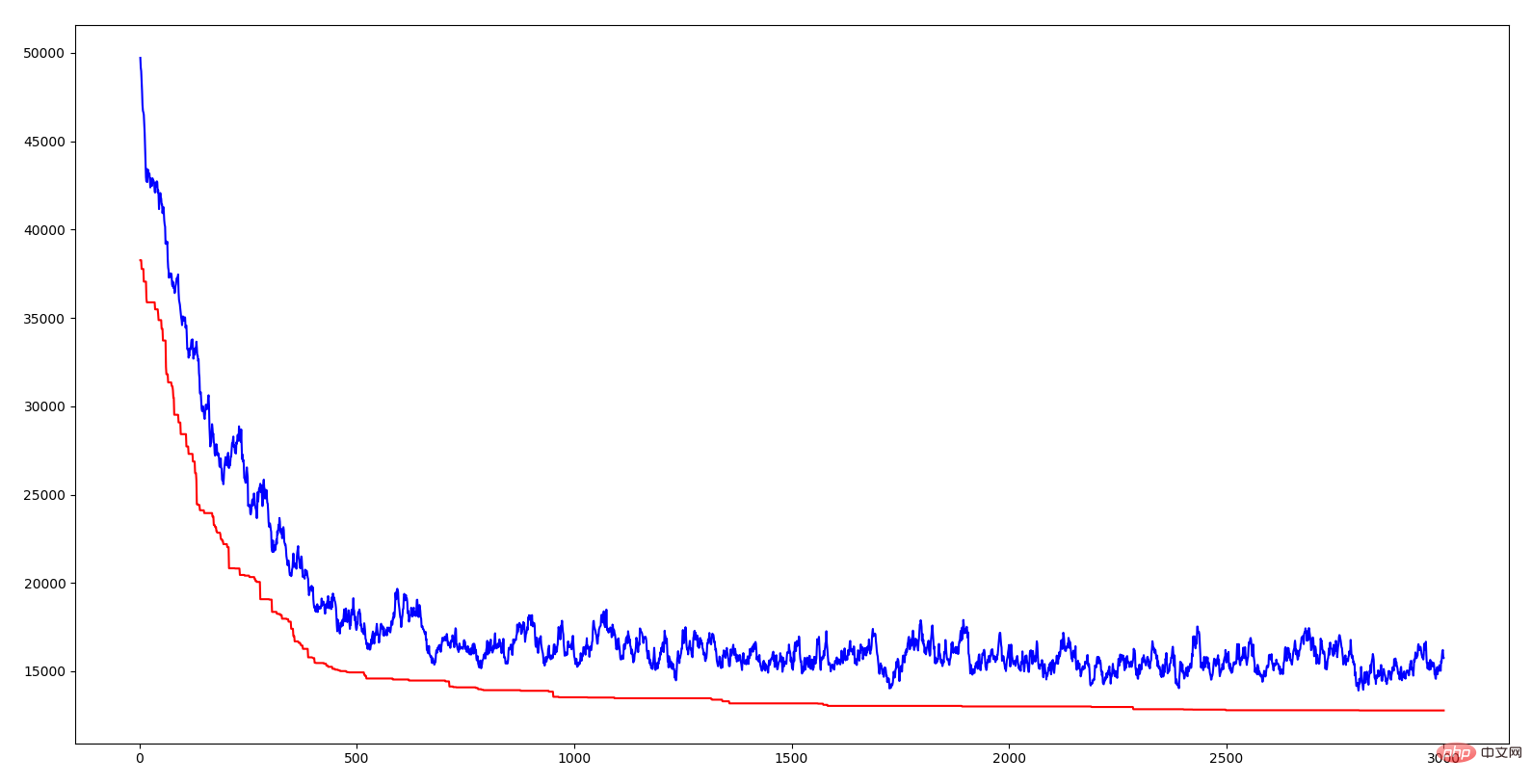
上圖橫座標是代數，縱座標是距離，紅色曲線是每一代的最優個體的距離，藍色曲線是每一代的平均距離。可以看出兩條線都呈現下降趨勢，也就是說都在進化。平均距離下降說明由於優良基因的出現（也就是某一段城市序列），使得這種優良的性狀很快就傳播到整個群體。就像自然界中的優勝劣汰一樣，具有適應環境的基因才能生存下來，相應的，生存下來的都是具有優良基因的。演算法中引入交叉率和變異率的意義就在於既要保證當前優良基因，又要試圖產生更優良的基因。如果所有個體都交叉，那麼有些優良的基因片段可能會遺失；如果都不交叉，那麼兩個優秀的基因片段無法組合為更優秀的基因；如果沒有變異，那就無法產生更適應環境的個體。不得不感嘆自然的智慧是如此強大。

上面說到的基因片段就是 TSP 中的一小段城市序列，當某一段序列的距離和相對較小時，就說明這段序列是這幾個城市的相對較好的遍歷順序。遺傳演算法透過將這些優秀的片段組合起來實現了 TSP 解的不斷優化。而組合的方法正是藉鏡自然的智慧，遺傳、變異、適者生存。

1.4 實驗總結

1、如何在演算法中實作「優勝劣汰」？

所謂優勝劣汰也就是優良的基因保留，不適應環境的基因淘汰。在上述 GA 演算法中，我使用的是輪盤賭，也就是在遺傳的步驟中（無論是否交叉），根據每個個體的適應度來挑選。這樣就能達到適應度高得個體有較多的後代，也就達到了優勝劣汰的目的。

在具體的實現過程中，我犯了個錯誤，起初在遺傳步驟篩選個體時，我每選出一個個體就將這個個體從群體中刪除。現在想想，這種做法十分愚蠢，儘管當時我已經實現了輪盤賭，但如果選出個體就刪除，那麼就會導致每個個體都會平等地生育後代，所謂的輪盤賭也不過是能讓適應度高的先進行遺傳。這種做法完全背離了「優勝劣汰」的初衷。正確的做法是選完個體進行遺傳後再重新放回群體，這樣才能保證適應度高的個體會進行多次遺傳，產生更多後代，將優良的基因更廣泛的播撒，同時不適應的個體會產生少量後代或直接被淘汰。

2 、如何保證演化一直是正向進行？

所謂正向進行也就是下一代的最優個體一定比上一代更適應或同等適應環境。我採用的方法是最優個體直接進入下一代，不參與交叉變異等操作。這樣能夠防止因這些操作而「污染」了當前最優秀的基因而導致反向演化的出現。

我在實作過程中還出現了另一個問題，是傳引用還是傳值所導致的。對個體的基因進行交叉和變異時用的是一個列表，Python 中傳列表時傳的實際上是一個引用，這樣就導致個體進行交叉和變異後會改變個體本身的基因。導致的結果就是進化非常緩慢，並且伴隨反向進化。

3、交叉如何實現？

選定一個個體的片段放入另一個體，並將不重複的基因的依序放入其他位置。

在實現這一步時，因為學生物時對真實染色體行為的固有認識，“同源染色體交叉互換同源區段”，導致我錯誤實現該功能。我只將兩個個體的相同位置的片段互換來完成交叉，顯然這樣的做法是錯誤的，這會導致城市的重複出現。

4、剛開始寫這個演算法時，我是半 OOP，半面向過程地寫。

後續測試過程中發現要改參數，更新個體資訊時很麻煩，於是全部改為 OOP，然後方便多了。對於這種模擬真實世界的問題，OOP 有很大的靈活性和簡單性。

5、如何防止局部最優解？

在測試過程中發現偶爾會出現局部最優解，在很長時間內不會繼續進化，而此時的解又離最優解較遠。即使是後續調整後，儘管離最優解近了，但依然是“局部最優”，因為還沒有達到最優。

演算法在起初會收斂得很快，而越往後就會越來越慢，甚至根本不動。因為到後期，所有個體都有著相對來說差不多的優秀基因，這時的交叉對於進化的作用就很弱了，進化的主要動力就成了變異，而變異就是一種暴力算法了。運氣好的話能很快變異出更好的個體，運氣不好就得一直等。

防止局部最優解的解決方法是增大族群規模，這樣就會有更多的個體變異，就會有更大可能性產生演化的個體。而增大族群規模的弊端是每一代的計算時間會變長，也就是說這兩者是互相抑制的。龐大的族群規模雖然最終能避免局部最優解，但是每一代的時間很長，需要很長時間才能求出最優解；而較小的種群規模雖然每一代計算時間快，但在若干代後就會陷入局部最優。

猜想一種可能的最佳化方法，在演化初期用較小的族群規模，以此來加快演化速度，當適應度達到某一閾值後，增加族群規模和變異率來避免局部最優解的出現。用這種動態調整的方法來權衡每一代運算效率和整體運算效率之間的平衡。

以上是如何使用Python實現遺傳演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章！