Python常見的歸一化方法有什麼作用

資料歸一化是深度學習資料預處理中非常關鍵的步驟，可以起到統一量綱，防止小資料被吞噬的作用。

一：歸一化的概念

歸一化就是把所有資料都轉換成[0,1]或[-1,1]之間的數，其目的是為了取消各維度資料之間的數量級差異，避免因為輸入輸出資料數量級差異大而造成網路預測誤差過大。

二：歸一化的作用

1. 為了後面資料處理的方便，歸一化可以避免一些不必要的數值問題。

2. 為了程式運行時收斂速度更快

3. #統一量綱。樣本資料的評量標準不一樣，需要對其量綱化，統一評量標準，這算是應用層面的需求。

4. 避免神經元飽和。是說當神經元的活化在接近0或1時，在這些區域，梯度幾乎為0，這樣在反向傳播過程中，局部梯度就會接近0，這樣非常不利於網路的訓練。

5. 保證輸出資料中數值小的不會被吞食。

三：歸一化的型別

1：線性歸一化

線性歸一化也稱為最小-最大規範化；離散標準化，是對原始資料的線性變換，將資料值對應到[0,1]之間。用公式表示為：

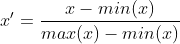
差標準化保留了原來資料中存在的關係，是消除量綱和資料取值範圍影響的最簡單的方法。程式碼實作如下：

def MaxMinNormalization(x,Max,Min):
    x = (x - Min) / (Max - Min);
    return x

適用範圍：比較適用在數值比較集中的情況

#缺點：

1. 如果max和min不穩定，很容易使得歸一化的結果不穩定，使得後續使用效果也不穩定。如果遇到超過目前屬性[min,max]取值範圍的時候，會造成系統報錯。需要重新確定min和max。

2. 如果數值集中的某個數值很大，則規範化後各值接近0，並且將會相差不大。 （如 1,1.2,1.3,1.4,1.5,1.6,10）這組數據。

2：零-平均值歸一化（Z-score標準化）

Z-score標準化也被稱為標準差標準化，經過處理的資料的平均值為0，標準差為1。其轉換公式為：

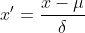
其中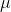為原始資料的平均值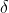，為原始資料的標準差，是目前用的最多的標準化公式

這種方法給予原始資料的平均值（mean）和標準差（standard deviation）進行資料的標準化。經過處理的資料符合標準常態分佈，即平均值為0，標準差為1，這裡的關鍵在於複合標準常態分佈

程式碼實作如下：

def Z_ScoreNormalization(x,mu,sigma):
    x = (x - mu) / sigma;
    return x

3：小數定標規範化

這種方法透過移動屬性值的小數位，將屬性值對應到[-1,1]之間，移動的小數位數取決於屬性值絕對值的最大值。轉換公式為：

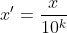
4:非線性歸一化 

這個方法包含log，指數，正切

適用範圍：經常用在資料分析比較大的場景，有些數值很大，有些很小，將原始值進​​行映射。

四：批次歸一化（BatchNormalization）

1：引入

在以往的神經網路訓練時，僅對輸入層資料進行歸一化處理，卻沒有在中間層進行歸一化處理。雖然我們對輸入資料進行了歸一化處理，但是輸入資料經過了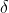這樣的矩陣乘法之後，其資料分佈很可能發生很大改變，並且隨著網路的層數不斷加深。數據分佈的變化將會越來越大。因此這種在神經網路中間層進行的歸一化處理，使得訓練效果更好的方法就被稱為批歸一化（BN）

2：BN演算法的優點

1. 減少了人為選擇參數

2. 減少了對學習率的要求，我們可以使用初始狀態下很大的學習率或使用較小的學習率時，演算法也能夠快速訓練收斂。

3. 破解了原來的資料分佈，一定程度上緩解了過擬合（防止每批訓練中某一個樣本經常被挑選到）

4. #減少梯度消失，加快收斂速度，提高訓練精度。

3：批次歸一化（BN）演算法流程

輸入：上一層輸出結果X={x1,x2,.....xm} ,學習參數，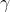

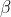
演算法流程：

1）計算上一層輸出資料的平均值：

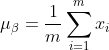
其中，m是這次訓練樣本batch的大小。

2）計算上一層輸出資料的標準差：

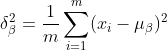
#3)歸一化處理得到

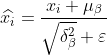
公式中的是為了避免分母為0而加進去接近於0的很小的值。

4）重構，將經過上面歸一化處理得到的資料進行重構，得到：

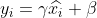
其中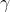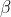，為可學習的參數。

以上是Python常見的歸一化方法有什麼作用的詳細內容。更多資訊請關注PHP中文網其他相關文章！