Python如何實作arctan換算角度

笛卡爾座標系

對於平面座標系，任一射線OP與x軸夾角θ的範圍，可以取[0,2π)或(-&pi ;,π]，如無特殊說明，我們統一使用後者。
將笛卡爾空間座標系中的點Pc = ( x , y , z ) 表示成球體座標系中的形式Ps = ( θ , ϕ , r )。

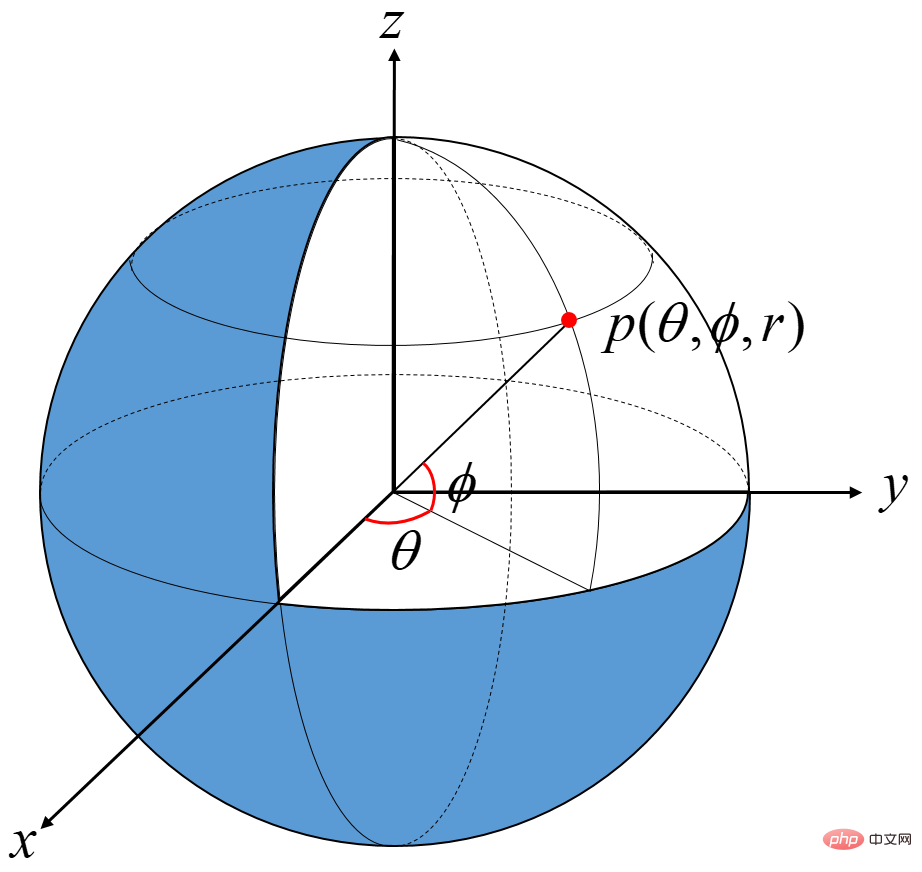
其中

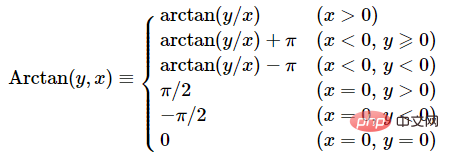
##根據球坐標的定義，要求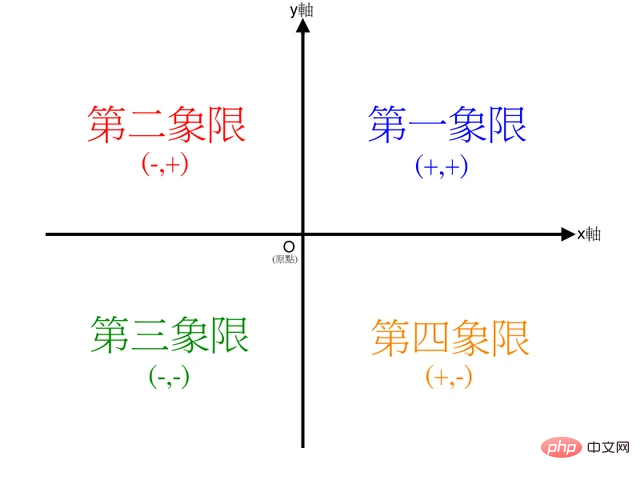θ∈[−π,π]，ϕ∈[−π/2,π/2] ，r∈[0 , ∞)

。

對於

θ
• ，正切函數的週期是π，因此反正切函數arctan 一般也只取一個週期，其定義域是R，值域是(−π /2 , π/2) 。為了解決這個問題，引入了 Arctan 函數，也就是 arctan2 函數。

atan2 函數的使用atan2(delta_y , delta_x)

• import math
  a = math.atan2(400,-692.820)
  # 2.6179936760992044
  angle = a/math.pi*180
  # 149.99998843242386

  atan 函數的使用atan(delta_y / delta_x)<pre class="brush:py;">import math delta_y = 400 delta_x = -692.820 if delta_x == 0: b = math.pi / 2.0 angle = b/math.pi*180 if delta_y == 0: angle = 0.0 elif delta_y &lt; 0: angle -= 180 else: b = math.atan(delta_y/delta_x) angle = b/math.pi*180 if delta_y &gt; 0 and delta_x &lt; 0: angle = angle + 180 if delta_y &lt; 0 and delta_x &lt; 0: angle = angle - 180 b,angle # (-0.5235989774905888, 149.99998843242386)</pre>atan和atan2 的異同

• 參數的個數不同

#兩者傳回值都是弧度

• 如果delta_x等於0，atan2仍然可以計算，但是atan 則需要提前判斷，否則就會導致程式出錯

象限的處理

• atan2(b,a)是4象限反正切，它的取值不僅取決於正切值b/a，還取決於點(b,a) 落入哪個象限：

• 當點(b,a) 落入第一象限(b>0, a>0)時，atan2(b,a)的範圍是0 ~ pi /2

當點(b,a)落入第二象限(b>0, a5cc264eb0c2caa0366c126b3140b350b0)時，atan2(b,a)的範圍是-pi/2～０

而atan(b/a) 僅根據正切值為a/b求對應的角度(可以看作只是2象限反正切)：

當b/a > 0 時，atan(b/a)取值範圍是0 ~ pi/2

當b/a 27ee3fc971958576d2cb6daca80e0bf60, a>0)###或###第四象限(bfaf8bb8ba0f442a0df2432c638c997200)###時，###atan2(b ,a) = atan(b/a) ###############點(b,a) 落入###第二象限(b>0, a1939fb0dc03ee0abc22f3b6e24d1a0b20，故atan(b/ a) 取值範圍是###0 ~ pi/2###，而此時atan2(b,a)的範圍是###-pi～-pi/2###，故atan(b/a ) 計算角度值要減180。 ############結論： atan 和 atan2函數，建議用 atan2函數###

以上是Python如何實作arctan換算角度的詳細內容。更多資訊請關注PHP中文網其他相關文章！