首次引入!用因果推理做部分可觀測強化學習
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB轉載
- 2023-04-15 11:07:021120瀏覽
這篇《Fast Counterfactual Inference for History-Based Reinforcement Learning》提出一種快速因果推理演算法,使得因果推理的計算複雜度大幅降低-降低到可以和online 強化學習結合的程度。
本文理論貢獻主要有兩點:
1、提出了時間平均因果效應的概念;
#2、將著名的後門準則從單變量介入效應估計推廣到多變量介入效應估計,稱為步進後門準則。
背景
需要準備關於部分可觀測強化學習和因果推理的基礎知識。這裡不做太多介紹,給幾個傳送門:
部分可觀測強化學習:
##POMDP解說https:// www.zhihu.com/zvideo/1326278888684187648
##因果推理:深度神經網路中的因果推理https://zhuanlan.zhihu .com/p/425331915
動機
從歷史資訊中擷取/編碼特徵是解決部分可觀測強化學習的基本手段。主流方法是使用sequence-to-sequence(seq2seq)模型來編碼歷史,例如領域內流行使用的LSTM/GRU/NTM/Transformer的強化學習方法都屬於這一類。這一類方法的共同之處在於,根據歷史資訊和學習訊號(環境獎勵)的相關性來編碼歷史,即一個歷史資訊的相關性越大所分配的權重也就越高。
然而,這些方法不能消除由取樣導致的混雜相關性。舉一個撿鑰匙開門的例子,如下圖:
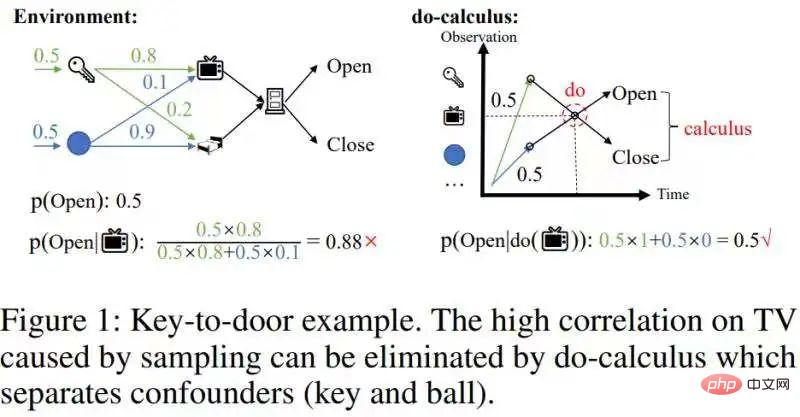
去除這種混雜的相關性。
這種混雜相關性可以透過因果推理中的do-calculus來去除[1]:分離可能造成混淆的後門變數鑰匙和球,從而切斷後門變數(鑰匙/球)和電視機之間的統計相關性,然後將p(Open| ,鑰匙/球)的條件機率關於後門變數(鑰匙/球)進行積分(Figure 1右圖),得到真實的效果p(Open|do( ))=0.5。由於有因果效應的歷史狀態相對稀疏,當我們去除混雜的相關性以後,可以大幅壓縮歷史狀態的規模。
因此,我們希望用因果推理來去除歷史樣本中混雜的相關性,然後再用seq2seq來編碼歷史,從而獲得更緊湊的歷史表徵。(本文動機)
[1]註:這裡考慮的是使用後門調整的do-calculus,附一個科普連結https://blog.csdn .net/qq_31063727/article/details/118672598# 在歷史序列中執行因果推理,不同於一般的因果推理問題。歷史序列中的變數既有時間維也有空間維度,即觀測-時間組合 以往的因果推理方法是基於單變量介入檢測,一次只能do一個變數。在具有龐大規模的歷史狀態上進行因果推理,將造成極高的時間複雜度,難以和online RL演算法結合。 [2]註:單變量介入因果效應的正式定義如下 如上圖所示,給定歷史 ,要估計對轉移變數 ##的因果效應,做以下兩步驟:1)幹預歷史狀態do ,2)以先前的歷史狀態 #為後門變量,為反應變量,計算如下積分即為所要求取的因果效應 既然單變量幹預檢測難以和online RL結合,那麼開發多變量幹預檢測方法就是必須的了。 本文的核心觀察(假設)是,因果狀態在空間維上稀疏。這個觀察是自然而普遍的,例如拿鑰匙開門,過程中會觀測到很多狀態,但鑰匙這個觀測值才決定了是否能開門,這個觀測值在所有觀測取值中佔比稀疏。利用這個稀疏性我們可以透過多變量幹預一次就篩選出大量沒有因果效應的歷史狀態。 但是時間維上因果效應並不稀疏,同樣是拿鑰匙開門,鑰匙可以被agent在絕大部分時刻都觀測到。時間維上因果效應的稠密性會妨礙我們進行多變量幹預──無法一次去除大量沒有因果效應的歷史狀態。 基於上述兩點觀察,我們的核心思路是,先在空間維上做推理,再在時間維上做推理。 利用空間維上的稀疏性大幅減少介入的次數。 為了單獨估計空間因果效應,我們提出先求取時間平均因果效應,就是把多個歷史狀態的因果效用在時間上進行平均(具體定義請見原文)。 基於這個idea,我們將問題聚焦:要解決的核心問題是如何計算幹預多個不同時間步上取值相同的變數(記作 ,可以看到,時間步靠後的 方法我們改進後門準則,提出一個適用於估計多變量聯合幹預效應估計的準則。對於任兩個被幹預的變數 (i 和 的
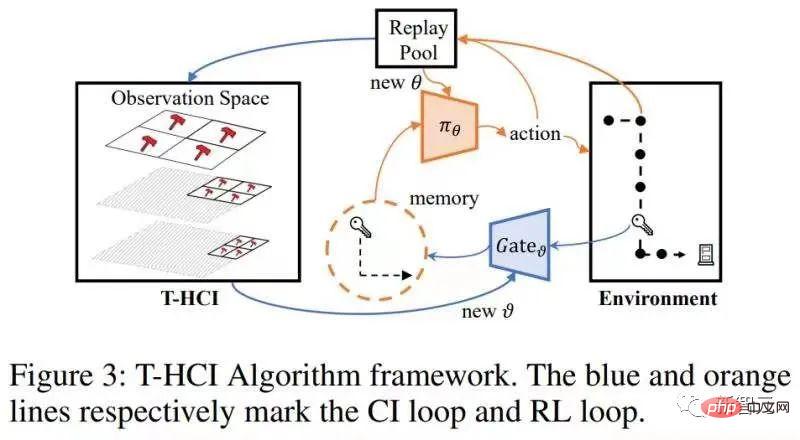
#上式使用了更一般的變數表示符X 。 具體到部分可觀測強化學習問題上,用觀測o取代上式的x後,有以下因果效應計算公式: Theorem 2. Given #至此,論文給出了計算空間因果效應(即時間平均因果效應)的公式,這一段方法將乾預的次數由O( 演算法結構圖如下 #演算法包含兩個loops,一個是T-HCI loop,一個是策略學習loop,兩者交換進行:在策略學習loop裡,agent被採樣學習一定回合數量,並將樣本存在replay pool中;在T-HCI loop中,利用儲存的樣本進行上述的因果推理過程。 Limitations:空間維上的因果推理對歷史規模的壓縮幅度已經夠大了。儘管時間維上做因果推理可以進一步壓縮歷史規模,但考慮到計算複雜度需要平衡,本文在時間維上保留了相關性推理(在有空間因果效應的歷史狀態上端到端使用LSTM),沒有使用因果推理。 實驗上驗證了三個點,回應了前面的claims:1) Can T-HCI improve the sample efficiency of RL methods? 2) Is the computational overhead of T-HCI acceptable in practice? 3) Can T-HCI mine observations with causal effects? 詳見論文的實驗章節,這裡就不佔用篇幅了。當然,有興趣的小夥伴還可私訊我/留言哦。 未來可拓展的方向 #說兩點,以拋磚引玉: 1、HCI不限於強化學習的類型。雖然本文研究的是online RL,但HCI也能自然地拓展到offline RL、model-based RL等等,甚至於可以考慮將HCI應用於模仿學習; 2.HCI可視為一種特殊的hard attention方法-有因果效性的序列點獲注意力權值1,反之獲注意力權值0。從這個角度來看,有些序列預測問題也可能嘗試使用HCI來處理。 困難
 ,其中o是觀測,t是時間戳(相較之下MDP就很友善了,馬可夫狀態只有空間維)。兩個維度的交疊,使得歷史觀測的規模相當龐大-以
,其中o是觀測,t是時間戳(相較之下MDP就很友善了,馬可夫狀態只有空間維)。兩個維度的交疊,使得歷史觀測的規模相當龐大-以 表示每個時間戳上的觀測取值個數,用T來表示時間總長度,則歷史狀態的值有
表示每個時間戳上的觀測取值個數,用T來表示時間總長度,則歷史狀態的值有  種(其中正體O( )為複雜度符號)。 [2]
種(其中正體O( )為複雜度符號)。 [2]

 )的聯合因果效應。這是因為後門準則不適用於多個歷史變數的聯合幹預:如下圖所示,考慮聯合幹預雙變量
)的聯合因果效應。這是因為後門準則不適用於多個歷史變數的聯合幹預:如下圖所示,考慮聯合幹預雙變量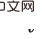 和
和
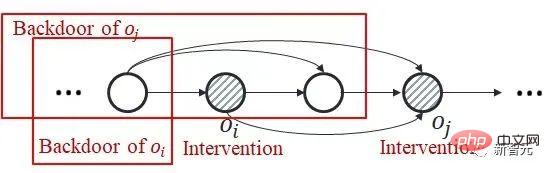
 的一部分後門變數裡包含了
的一部分後門變數裡包含了 ,兩者不存在公共的後門變數。
,兩者不存在公共的後門變數。  和
和 步進後門調整準則(step-backdoor adjustment formula)
步進後門調整準則(step-backdoor adjustment formula)

 該準則分離了,介於相鄰兩個時間步的變數之間的其他變量,稱為步進後門變數。在滿足這個準則的因果圖中,我們可以估計任兩個被幹預變數的聯合因果效應。包括兩個步驟:step 1、以時間步上小於i的變數作為後門變量,估計do
該準則分離了,介於相鄰兩個時間步的變數之間的其他變量,稱為步進後門變數。在滿足這個準則的因果圖中,我們可以估計任兩個被幹預變數的聯合因果效應。包括兩個步驟:step 1、以時間步上小於i的變數作為後門變量,估計do
 #因果效應;step 2、以取定的
#因果效應;step 2、以取定的 後門變數與取定的
後門變數與取定的 為條件,以介於
為條件,以介於 與之間的變數為新的關於
與之間的變數為新的關於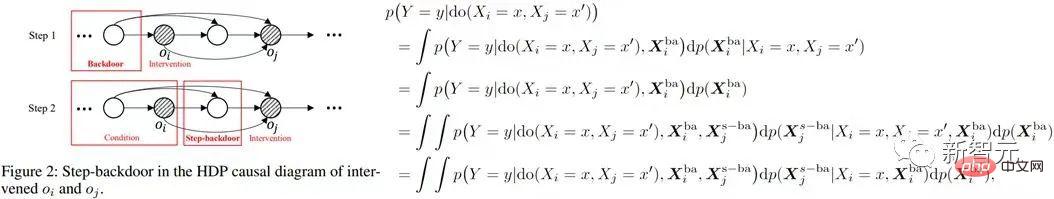 的後門變數(即關於
的後門變數(即關於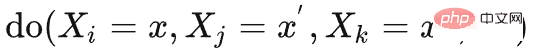 條件因果效應。則聯合因果效應為這兩部分的乘積積分。步進後門準則將普通的後門準則使用了兩步,如下圖所示
條件因果效應。則聯合因果效應為這兩部分的乘積積分。步進後門準則將普通的後門準則使用了兩步,如下圖所示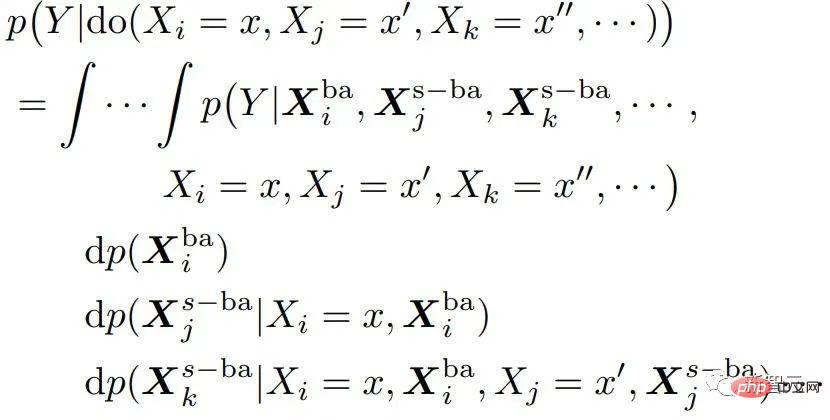
 and
and  , the causal effect of Do(o) can be estimated by
, the causal effect of Do(o) can be estimated by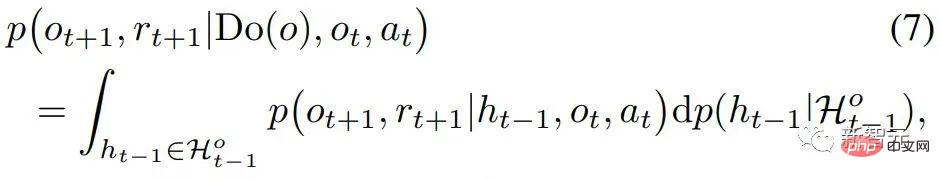
 )降低為O(
)降低為O( )。接下來,就是利用(本章開頭提及)空間因果效應的稀疏性,進一步對介入次數完成指數級縮減。將對一個觀測的干預替換為對一個觀測子空間的干預——這是一個利用稀疏性加速計算的通常思路(請見原文)。在本文中,發展了一個稱為Tree-based history counterfactual inference (T-HCI)的快速反事實推理演算法,這裡不作贅述(詳見原文)。其實基於步進後門準則後續還可以開發很多歷史因果推理演算法,T-HCI只是其中的一個。最後的結果是Proposition 3 (Coarse-to-fine CI). If
)。接下來,就是利用(本章開頭提及)空間因果效應的稀疏性,進一步對介入次數完成指數級縮減。將對一個觀測的干預替換為對一個觀測子空間的干預——這是一個利用稀疏性加速計算的通常思路(請見原文)。在本文中,發展了一個稱為Tree-based history counterfactual inference (T-HCI)的快速反事實推理演算法,這裡不作贅述(詳見原文)。其實基於步進後門準則後續還可以開發很多歷史因果推理演算法,T-HCI只是其中的一個。最後的結果是Proposition 3 (Coarse-to-fine CI). If , the number of interventions for coarse-to-fine CI is
, the number of interventions for coarse-to-fine CI is #)。
#)。 
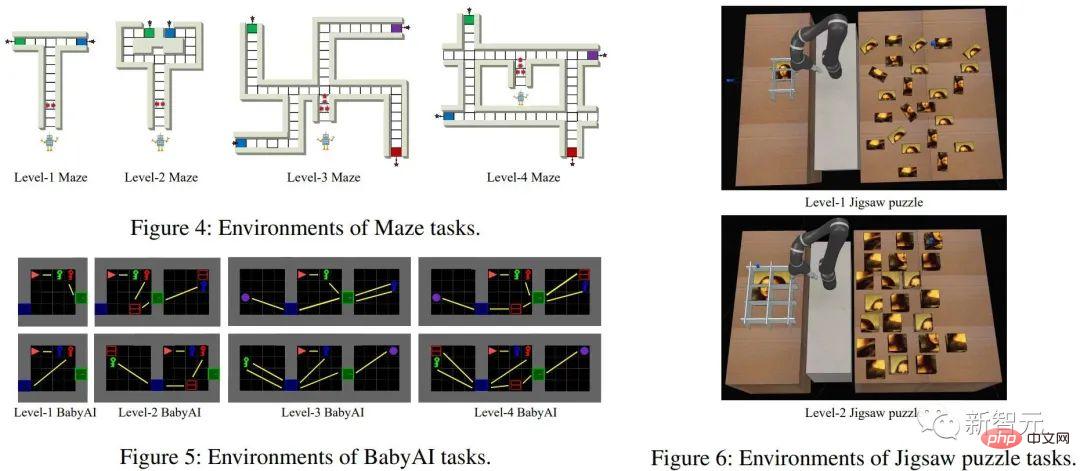
驗證
以上是首次引入!用因果推理做部分可觀測強化學習的詳細內容。更多資訊請關注PHP中文網其他相關文章!

