NP完備破解羊了個羊？

近日，羊了個羊火遍了網絡，一時間關於第二關怎樣難、如何通關的文章也多了起來，但是從計算複雜性（computational complexity）的角度討論遊戲難度的文章應該還沒有，所以這次我也寫一篇關於計算複雜度的文章來碰瓷。

遊戲的機制是比較簡單的，簡單說來就是地圖上有一些不同類型的方塊，玩家可以選擇方塊放入自己的槽位中（槽位有上限，是個常數），如果插槽中有三個相同類型的方塊就消去，遊戲目標是消去所有方塊。遊戲的困難在於地圖上的方塊是堆疊起來的，被疊在下方的方塊不能被選擇，只有在上方的方塊被放入槽位後才能被選擇（也就是解鎖），有時被疊在下方的方塊的類型都由於被遮蔽而不可知。

事實上，羊了個羊與有些小遊戲的機制很類似，而其中許多小遊戲已經被證明是NP-complete 的，所以我們比較確信也能證明推廣了的羊了個羊是NP-complete 的。這裡我們給一個比較弱的、簡單的歸約構造，來說明推廣的羊了個羊遊戲是 NP-complete。這裡我們說的推廣是指方塊類型的數量不限制於常數，被遮擋的方塊類型是確定的且已知的，槽位數量固定為3（槽位數量是其他常數也可以用類似方法，只要在遊戲初期迫使玩家拿一個特殊類型的方塊，而在遊戲最後才能消去，整個過程中這個方塊佔用了一個槽位，相當於少了一個槽位）。當然，這裡我們不考慮遊戲道具的影響。

本文的歸約主要抄襲的是Computational Complexity of Games and Puzzles 網頁上證明Mah-Jongg 遊戲（一個類似連連看的遊戲，有的地方也叫麻將）是NP -complete 的歸約。

我們仍然使用 3-SAT 這個經典的 NP-complete 問題作為歸約問題。我們對於 3-SAT 公式中的每個變數設定 3 個方塊堆，一個方塊堆用於模擬變數的賦值（TRUE or FALSE），一個方塊堆對應於賦值為 FALSE，一個堆對應於賦值為 TRUE。模擬變數的賦值方塊堆有兩層，第一層是 4 個一樣的對應於變數的方塊，第二層包含變數被賦值為 TRUE 和 FALSE 的方塊各一個以及填滿方塊。對應於賦值為FALSE 的方塊堆通常是多層的（也可能退化為一層），頂層包含兩個對應於變數被賦值為FALSE 的方塊（用於配合之前賦值方塊堆使用），下層包含對應於子句的方塊（對應子句中變數以非的形式出現）以及填滿方塊。對應於賦值為 TRUE 的方塊堆的結構是類似的。最後，還有一個用來驗證解的方塊堆，這個堆是多層結構，頂部包含了對應於子句的方塊，中間是對應於變數的方塊，底部是對應於子句的方塊。

我們用一個具體的例子來描述這個歸約，假設 3-SAT 的實例是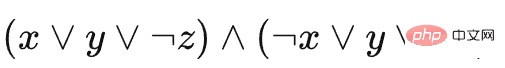。那麼對於的羊了個羊遊戲的實例如下（為了能表述每個方塊的類型和堆疊情況，我們使用側面視圖的方式展示）

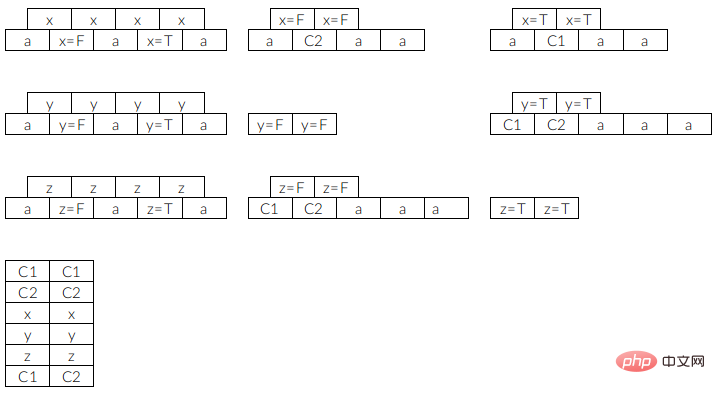
#其中C1 表示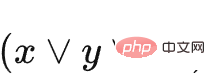，C2 表示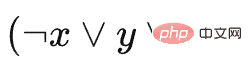，a 是填滿方塊，a 方塊沒有壓住任何方塊，所以可以留到最後再全部消去而不影響其他方塊。注意這裡我們設定的插槽數量是 3，也就是說選擇某個方塊放入槽後就必須要消除這個類型的方塊，否則就無法繼續遊戲了。

如果公式可滿足，那麼可以依照滿足時各變數的賦值來消除方塊。例如假設xyz 全賦值為FALSE，那麼我們就對應消除最左邊的三個x y 和z，這樣一來，第二層的方塊x=F y=F 和z=F 就被解鎖，我們就可以消去所有x=F y=F z=F 方塊，接著一個C1 方塊和兩個C2 方塊就解鎖，然後就能配合最下方的驗證方塊堆，消去驗證堆的頂部兩層，而後中間的變數xyz 方塊也馬上能消去，最後就沒有什麼限制了，所有的方塊都能夠被消去。

反過來，如果所有方塊可以消去（也就是該關卡可以通關），那麼公式可滿足。注意到驗證堆中的變數xyz 的方塊想要被消去，必須上部的C1 C2 子句方塊都先消去，而子句方塊又受限於賦值方塊，賦值方塊受限於變數方塊，變數方塊的擺放方式決定了在變數賦值時，每個變數只能賦為FALSE 或TRUE 中的一個（具體來說，在遊戲初期4 個x 方塊中任意消去3 個後，方塊x=F 和x=T 中必然有一個未被解鎖）。這就意味著方塊消去的順序蘊含了一個滿足公式的賦值。

這也就是說 3-SAT 公式可滿足的充分必要條件是對應的羊了個羊遊戲實例可通關。而羊了個羊顯然屬於NP，因為能在多項式時間內判定一個操作序列是否能消去所有方塊，從而我們就證明了下面的命題：

命題：在所有被遮蔽的方塊類型是確定且已知的條件下，推廣的羊了個羊遊戲屬於NP-complete。

用非人話來說就是，你沒有辦法設計一個多項式時間複雜度的演算法來判斷任意推廣的羊了個羊關卡是否有解，除非P=NP （這個只有4 個字元的等式價值一個土地獎和100 萬美元，所以別去閒著沒事就想著嘗試證明或證否）。用人話來說就是，即使被遮擋的方塊類型是確定的且已知的，計算機也仍然（幾乎）無法快速地判斷羊了個羊是否能通關。

以上是NP完備破解羊了個羊？的詳細內容。更多資訊請關注PHP中文網其他相關文章！