Python影像處理:頻域濾波降噪和影像增強
- PHPz轉載
- 2023-04-14 22:16:011988瀏覽
影像處理已經成為我們日常生活中不可或缺的一部分,涉及社交媒體和醫學影像等各個領域。透過數位相機或衛星照片和醫學掃描等其他來源獲得的影像可能需要預處理以消除或增強雜訊。頻域濾波是一種可行的解決方案,它可以在增強影像銳利化的同時消除雜訊。
快速傅立葉變換(FFT)是一種將影像從空間域轉換到頻率域的數學技術,是影像處理中進行頻率變換的關鍵工具。透過利用影像的頻域表示,我們可以根據影像的頻率內容有效地分析影像,從而簡化濾波程式的應用以消除雜訊。本文將討論影像從FFT到逆FFT的頻率變換所涉及的各個階段,並結合FFT位移和逆FFT位移的使用。
本文使用了三個Python函式庫,分別是openCV、Numpy和Matplotlib。
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('sample.png',0) # Using 0 to read image in grayscale mode
plt.imshow(img, cmap='gray')#cmap is used to specify imshow that the image is in greyscale
plt.xticks([]), plt.yticks([])# remove tick marks
plt.show()

1、快速傅立葉轉換(FFT)
快速傅立葉轉換( FFT)是一種廣泛應用的數學技術,它允許影像從空間域轉換到頻率域,是頻率變換的基本組成部分。利用FFT分析,可以得到影像的週期性,並將其劃分為不同的頻率分量,產生影像頻譜,顯示每個影像各自頻率成分的振幅和相位。
f = np.fft.fft2(img)#the image 'img' is passed to np.fft.fft2() to compute its 2D Discrete Fourier transform f
mag = 20*np.log(np.abs(f))
plt.imshow(mag, cmap = 'gray') #cmap='gray' parameter to indicate that the image should be displayed in grayscale.
plt.title('Magnitude Spectrum')
plt.xticks([]), plt.yticks([])
plt.show()
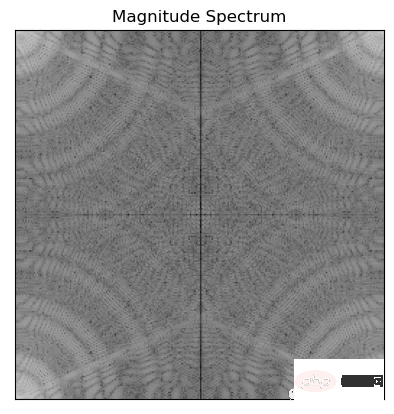
上面程式碼使用np.abs()計算傅立葉變換f的幅度,np.log()轉換為對數刻度,然後乘以20得到以分貝為單位的幅度。這樣做是為了讓幅度譜更容易被視覺化和解釋。
2、FFT位移
為了讓濾波演算法套用到影像,利用FFT移位將影像的零頻率成分被移到頻譜的中心
fshift = np.fft.fftshift(f)
mag = 20*np.log(np.abs(fshift))
plt.imshow(mag, cmap = 'gray')
plt.title('Centered Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()
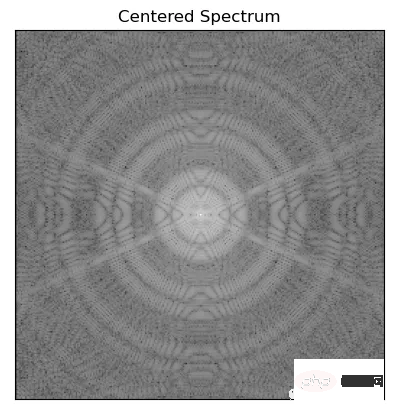
3、濾波
頻率變換的一個目的是使用各種濾波演算法來降低雜訊和提高影像品質。兩種最常用的影像銳化濾波器是Ideal high-pass filter 和Gaussian high-pass filter。這些濾波器都是使用的透過快速傅立葉變換(FFT)方法獲得的圖像的頻域表示。
Ideal high-pass filter(理想濾波器) 是一種無限長的、具有無限頻帶寬和理想通帶和阻帶響應的濾波器。其通帶內所有頻率的訊號都完全傳遞,而阻帶內所有頻率的訊號則完全被抑制。
在頻域上,理想濾波器的幅頻響應為:
- 在通帶內,幅頻響應為1
- 在阻帶內,幅頻響應為0
在時域上,理想濾波器的衝激響應為:
- 在通帶內,衝激響應為一個無限長的單位衝激函數序列
- 在阻帶內,衝激響應為零
由於理想濾波器在頻域上具有無限頻寬,因此它無法在實際應用中實現。實際使用的數位濾波器通常是基於理想濾波器的逼近,所以才被成為只是一個Ideal。
高斯高通濾波器(Gaussian high-pass filter)是一種在數位影像處理中常用的濾波器。它的作用是在影像中保留高頻細節訊息,並抑制低頻訊號。此濾波器基於高斯函數,具有光滑的頻率響應,可適應各種影像細節。
高斯高通濾波器的頻率響應可以表示為:
H(u,v) = 1 - L(u,v)
其中,L(u, v)是一個低通濾波器,它可以用高斯函數表示。將低通濾波器的響應從1中減去,可以得到一個高通濾波器的響應。在實際中,通常會使用不同的參數設定來調整高斯函數,以達到不同的濾波效果。
圓形遮罩(disk-shaped images)是用來定義在影像中進行傅立葉變換時要保留或抑制的頻率分量。在這種情況下,理想濾波器通常是指理想的低通或高通濾波器,可以在頻域上選擇保留或抑制特定頻率範圍內的訊號。將這個理想濾波器套用在影像的傅立葉變換後,再進行逆變換,可以得到過濾器處理後的影像。
具體的細節我們就不介紹了,直接來看程式碼:
下面函數是產生理想高通和低通濾波器的圓形遮罩
import math def distance(point1,point2): return math.sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2) def idealFilterLP(D0,imgShape): base = np.zeros(imgShape[:2]) rows, cols = imgShape[:2] center = (rows/2,cols/2) for x in range(cols): for y in range(rows): if distance((y,x),center) < D0: base[y,x] = 1 return base def idealFilterHP(D0,imgShape): base = np.ones(imgShape[:2]) rows, cols = imgShape[:2] center = (rows/2,cols/2) for x in range(cols): for y in range(rows): if distance((y,x),center) < D0: base[y,x] = 0 return base
下面函數產生一個高斯高、低通濾波器與所需的圓形遮罩
import math def distance(point1,point2): return math.sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2) def gaussianLP(D0,imgShape): base = np.zeros(imgShape[:2]) rows, cols = imgShape[:2] center = (rows/2,cols/2) for x in range(cols): for y in range(rows): base[y,x] = math.exp(((-distance((y,x),center)**2)/(2*(D0**2)))) return base def gaussianHP(D0,imgShape): base = np.zeros(imgShape[:2]) rows, cols = imgShape[:2] center = (rows/2,cols/2) for x in range(cols): for y in range(rows): base[y,x] = 1 - math.exp(((-distance((y,x),center)**2)/(2*(D0**2)))) return base
過濾範例
fig, ax = plt.subplots(2, 2) # create a 2x2 grid of subplots
fig.suptitle('Filters') # set the title for the entire figure
# plot the first image in the top-left subplot
im1 = ax[0, 0].imshow(np.abs(idealFilterLP(50, img.shape)), cmap='gray')
ax[0, 0].set_title('Low Pass Filter of Diameter 50 px')
ax[0, 0].set_xticks([])
ax[0, 0].set_yticks([])
# plot the second image in the top-right subplot
im2 = ax[0, 1].imshow(np.abs(idealFilterHP(50, img.shape)), cmap='gray')
ax[0, 1].set_title('High Pass Filter of Diameter 50 px')
ax[0, 1].set_xticks([])
ax[0, 1].set_yticks([])
# plot the third image in the bottom-left subplot
im3 = ax[1, 0].imshow(np.abs(gaussianLP(50 ,img.shape)), cmap='gray')
ax[1, 0].set_title('Gaussian Filter of Diameter 50 px')
ax[1, 0].set_xticks([])
ax[1, 0].set_yticks([])
# plot the fourth image in the bottom-right subplot
im4 = ax[1, 1].imshow(np.abs(gaussianHP(50 ,img.shape)), cmap='gray')
ax[1, 1].set_title('Gaussian Filter of Diameter 50 px')
ax[1, 1].set_xticks([])
ax[1, 1].set_yticks([])
# adjust the spacing between subplots
fig.subplots_adjust(wspace=0.5, hspace=0.5)
# save the figure to a file
fig.savefig('filters.png', bbox_inches='tight')

相乘过滤器和移位的图像得到过滤图像
为了获得具有所需频率响应的最终滤波图像,关键是在频域中对移位后的图像与滤波器进行逐点乘法。
这个过程将两个图像元素的对应像素相乘。例如,当应用低通滤波器时,我们将对移位的傅里叶变换图像与低通滤波器逐点相乘。
此操作抑制高频并保留低频,对于高通滤波器反之亦然。这个乘法过程对于去除不需要的频率和增强所需的频率是必不可少的,从而产生更清晰和更清晰的图像。
它使我们能够获得期望的频率响应,并在频域获得最终滤波图像。
4、乘法滤波器(Multiplying Filter)和平移后的图像(Shifted Image)
乘法滤波器是一种以像素值为权重的滤波器,它通过将滤波器的权重与图像的像素值相乘,来获得滤波后的像素值。具体地,假设乘法滤波器的权重为h(i,j),图像的像素值为f(m,n),那么滤波后的像素值g(x,y)可以表示为:
g(x,y) = ∑∑ f(m,n)h(x-m,y-n)
其中,∑∑表示对所有的(m,n)进行求和。
平移后的图像是指将图像进行平移操作后的结果。平移操作通常是指将图像的像素沿着x轴和y轴方向进行平移。平移后的图像与原始图像具有相同的大小和分辨率,但它们的像素位置发生了变化。在滤波操作中,平移后的图像可以用于与滤波器进行卷积运算,以实现滤波操作。
此操作抑制高频并保留低频,对于高通滤波器反之亦然。这个乘法过程对于去除不需要的频率和增强所需的频率是必不可少的,从而产生更清晰和更清晰的图像。
它使我们能够获得期望的频率响应,并在频域获得最终滤波图像。
fig, ax = plt.subplots()
im = ax.imshow(np.log(1+np.abs(fftshifted_image * idealFilterLP(50,img.shape))), cmap='gray')
ax.set_title('Filtered Image in Frequency Domain')
ax.set_xticks([])
ax.set_yticks([])
fig.savefig('filtered image in freq domain.png', bbox_inches='tight')
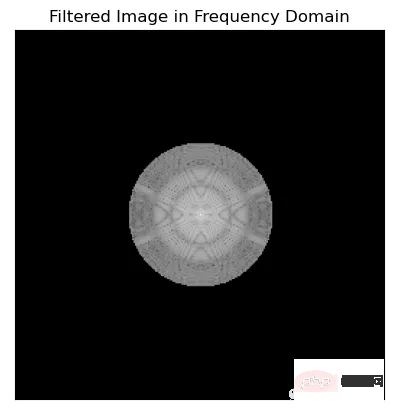
在可视化傅里叶频谱时,使用np.log(1+np.abs(x))和20*np.log(np.abs(x))之间的选择是个人喜好的问题,可以取决于具体的应用程序。
一般情况下会使用Np.log (1+np.abs(x)),因为它通过压缩数据的动态范围来帮助更清晰地可视化频谱。这是通过取数据绝对值的对数来实现的,并加上1以避免取零的对数。
而20*np.log(np.abs(x))将数据按20倍缩放,并对数据的绝对值取对数,这可以更容易地看到不同频率之间较小的幅度差异。但是它不会像np.log(1+np.abs(x))那样压缩数据的动态范围。
这两种方法都有各自的优点和缺点,最终取决于具体的应用程序和个人偏好。
5、逆FFT位移
在频域滤波后,我们需要将图像移回原始位置,然后应用逆FFT。为了实现这一点,需要使用逆FFT移位,它反转了前面执行的移位过程。
fig, ax = plt.subplots()
im = ax.imshow(np.log(1+np.abs(np.fft.ifftshift(fftshifted_image * idealFilterLP(50,img.shape)))), cmap='gray')
ax.set_title('Filtered Image inverse fft shifted')
ax.set_xticks([])
ax.set_yticks([])
fig.savefig('filtered image inverse fft shifted.png', bbox_inches='tight')

6、快速傅里叶逆变换(IFFT)
快速傅里叶逆变换(IFFT)是图像频率变换的最后一步。它用于将图像从频域传输回空间域。这一步的结果是在空间域中与原始图像相比,图像减少了噪声并提高了清晰度。
fig, ax = plt.subplots()
im = ax.imshow(np.log(1+np.abs(np.fft.ifft2(np.fft.ifftshift(fftshifted_image * idealFilterLP(50,img.shape))))), cmap='gray')
ax.set_title('Final Filtered Image In Spatial Domain')
ax.set_xticks([])
ax.set_yticks([])
fig.savefig('final filtered image.png', bbox_inches='tight')

总结
我们再把所有的操作串在一起显示,
函数绘制所有图像
def Freq_Trans(image, filter_used): img_in_freq_domain = np.fft.fft2(image) # Shift the zero-frequency component to the center of the frequency spectrum centered = np.fft.fftshift(img_in_freq_domain) # Multiply the filter with the centered spectrum filtered_image_in_freq_domain = centered * filter_used # Shift the zero-frequency component back to the top-left corner of the frequency spectrum inverse_fftshift_on_filtered_image = np.fft.ifftshift(filtered_image_in_freq_domain) # Apply the inverse Fourier transform to obtain the final filtered image final_filtered_image = np.fft.ifft2(inverse_fftshift_on_filtered_image) return img_in_freq_domain,centered,filter_used,filtered_image_in_freq_domain,inverse_fftshift_on_filtered_image,final_filtered_image
使用高通、低通理想滤波器和高斯滤波器的直径分别为50、100和150像素,展示它们对增强图像清晰度的影响。
fig, axs = plt.subplots(12, 7, figsize=(30, 60))
filters = [(f, d) for f in [idealFilterLP, idealFilterHP, gaussianLP, gaussianHP] for d in [50, 100, 150]]
for row, (filter_name, filter_diameter) in enumerate(filters):
# Plot each filter output on a separate subplot
result = Freq_Trans(img, filter_name(filter_diameter, img.shape))
for col, title, img_array in zip(range(7),
["Original Image", "Spectrum", "Centered Spectrum", f"{filter_name.__name__} of Diameter {filter_diameter} px",
f"Centered Spectrum multiplied by {filter_name.__name__}", "Decentralize", "Processed Image"],
[img, np.log(1+np.abs(result[0])), np.log(1+np.abs(result[1])), np.abs(result[2]), np.log(1+np.abs(result[3])),
np.log(1+np.abs(result[4])), np.abs(result[5])]):
axs[row, col].imshow(img_array, cmap='gray')
axs[row, col].set_title(title)
plt.tight_layout()
plt.savefig('all_processess.png', bbox_inches='tight')
plt.show()

可以看到,當改變圓形遮罩的直徑時,對影像清晰度的影響會有所不同。隨著直徑的增加,更多的頻率被抑制,產生更平滑的圖像和更少的細節。減小直徑允許更多的頻率通過,從而產生更清晰的圖像和更多的細節。為了達到理想的效果,選擇合適的直徑是很重要的,因為使用太小的直徑會導致過濾器不夠有效,而使用太大的直徑會導致失去太多的細節。
一般來說,高斯濾波器由於其平滑性和穩健性,更常用於影像處理任務。在某些應用中,需要更尖銳的截止,理想濾波器可能更適合。
利用FFT修改影像頻率是一種有效的降低雜訊和提高影像銳利度的方法。這包括使用FFT將影像轉換到頻域,使用適當的技術過濾噪聲,並使用反FFT將修改後的影像轉換回空間域。透過理解和實現這些技術,我們可以提高各種應用程式的影像品質。
以上是Python影像處理:頻域濾波降噪和影像增強的詳細內容。更多資訊請關注PHP中文網其他相關文章!

