電晶體救命稻草來了：3D堆疊CMOS，摩爾定律又續10年？

晶體管，被譽為「20世紀最偉大的發明」。

它的出現為積體電路、微處理器以及電腦記憶體的產生奠定了基礎。

1965年，「摩爾定律」的提出成為半導體產業幾十年來的金科玉律。

它表明，每隔18~24 個月，封裝在微晶片上的電晶體數量便會增加一倍，晶片的性能也會隨之翻一番。

然而，隨著新製程節點的不斷推出，電晶體中原子的數量已經越來越少，種種物理極限制約著摩爾定律的進一步發展。

甚至有人認為摩爾定律已經結束了。

因此，為了「拯救」摩爾定律，工程師必須改變電晶體結構，繼續減少面積和功耗，並提高其性能。

20世紀下半葉，主要流行平面電晶體設計（Planar Transistor）。跨入2010年代，3D鰭形元件（3D fin-shaped devices）逐漸取代了平面設計。

現在，一種全新的電晶體設計結構，即全環繞閘極電晶體（GAA）成為FinFET的繼任者，並且即將投入生產。

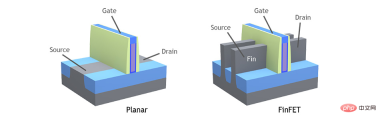
但是，我們必須看得更遠。因為即便是英特爾提出的這種全新電晶體架構RibbonFET，我們在縮小尺寸上的能力也有其限制。

要相信， 3D堆疊的互補金屬氧化物半導體(CMOS) 或CFET（互補場效電晶體）將是把摩爾定律延伸到下一個十年的關鍵。

電晶體的演化

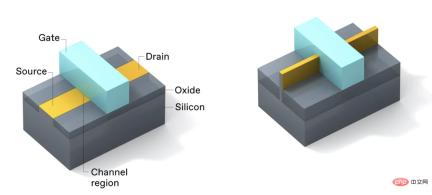
每個金屬氧化物半導體場效電晶體（MOSFET）都有一套相同的基本元件:

閘極疊層(gate stack) 、通道區(channel region) 、源極(source) 、汲極(drain)

#源極和汲極經過化學摻雜，使它們要麼富含移動電子(n型)，要麼缺乏它們(p型)。溝道區具有與源極和汲極相反的摻雜。

2011年之前的先進微處理器中的平面版本電晶體中，MOSFET的閘極疊層剛好在通道區的上方，是用來將電場投射到通道區域。

向閘極施加足夠大的電壓(相對於源極) ，就會在通道區域形成一層移動電荷載子，這樣就能讓電流在源極和汲極之間流動。

為了縮小平面電晶體設計的尺寸，一種「短溝道效應」成為物理家們的焦點。

因為隨著製程技術不斷提升時，電晶體中閘極的寬度被擠壓的越來越小。要知道，當這個閘極低於20nm時，就會對電流失控，源極的電流會穿透閘極，直接到達汲極。

這時，就會出現「漏電」現象，會讓晶片耗急遽上升。

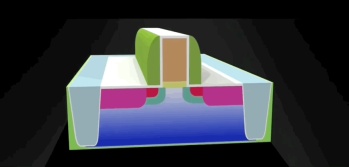
為了解決這個問題，一種全新的FinFET電晶體技術提出了。它將閘極包裹在三個側面的通道周圍，以提供更好的靜電控制。

FinFET與上一代平面架構相同的效能水準下將功耗降低了約 50%。 FinFET 的切換速度也更快，效能提升了 37%。

2011年，英特爾在推出的22nm節點上引入了FinFET，並將其用在了第三代酷睿處理器的生產。

從那時起，FinFET就成為摩爾定律的主力。

然而，我們在轉向FinFET的同時，也失去了一些東西。

在平面元件中，電晶體的寬度由微影定義，因此它是一個高度靈活的參數。

但在 FinFET 中，電晶體寬度以離散增量（discrete increments）的形式出現，即每次新增一個鰭。這一特性通常被稱為鰭量化（fin quantization）。

儘管 FinFET 很靈活，但鰭量化仍然是一個重要的設計限制。圍繞它的設計規則，以及增加更多鰭片以提高性能的願望增加了邏輯單元的整體面積，並使將單個晶體管變成完整邏輯電路的互連堆疊複雜化。

它也增加了電晶體的電容，從而降低了它的開關速度。因此，雖然FinFET作為業界主力為我們提供了很好的服務，但仍需要一種新的、更精細的方法。

正是這種方法引導物理學家發明了即將推出的3D電晶體－RibbonFET。

在RibbonFET中，閘極環繞電晶體通道區域以增強對電荷載子的控制。新結構還可以實現更好的性能和更精細的優化。

具體來講，閘極完全圍繞著通道，對通道內的電荷載子提供更嚴格的控制，這些通道現在由奈米級矽帶形成。

使用這些奈米帶（奈米片），就可以再次使用光刻技術根據需要改變電晶體的寬度。

移除量化限制後，便可為應用程式產生適當大小的寬度。這樣就使我們能夠平衡功率、性能和成本。

更重要的是，透過堆疊和平行操作，裝置可以驅動更多的電流，不增加面積的情況下也能提升效能。

因此，英特爾認為RibbonFET是合理功率下實現更高性能的最佳選擇。

他們將在2024年Intel 20A製程上引進RibbonFET結構。

3D堆疊CMOS

平面型、FinFET 和RibbonFET 電晶體的一個共同點是，都使用CMOS 技術，如前所述，CMOS 由n 型和p 型電晶體組成。這項技術在20世紀80年代開始成為主流，因為它比其他替代技術吸收的電流少得多。更少的電流意味著更高的工作頻率和更高的電晶體密度。

#

迄今為止，所有的 CMOS 技術將標準的 NMOS 和 PMOS 電晶體對並排放置。但在2019年 IEEE 國際電子元件會議(IEDM)的主題演講中，提出了一個「3D堆疊」電晶體的概念，將 NMOS 電晶體置於 PMOS 電晶體之上。

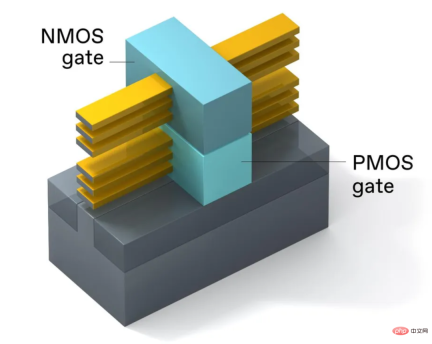
在IEDM 2020上，提出了第一個使用這種3D技術的邏輯電路的設計的逆變器。 3D 堆疊 CMOS 有效地減少了一半的逆變器足跡，將電晶體面積密度提升一倍，進一步推高了摩爾定律的極限。

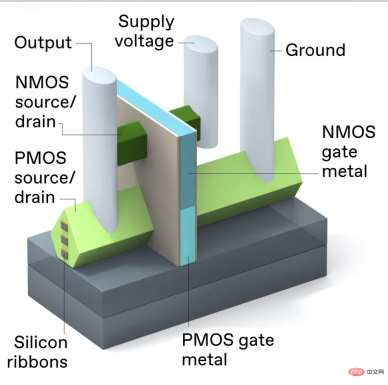
3D 堆疊 CMOS結構，將 PMOS 元件放置在 NMOS 元件的頂部，總面積與一個 RibbonFET 面積相同。 NMOS 和PMOS 閘使用不同的金屬材質

要利用3D堆疊CMOS，要解決許多製程整合上的挑戰，其中一些涉及CMOS加工製造的極限。

如何實作呢？自對齊的3D CMOS的製造始於矽晶片。在晶片上，我們沉積了一層又一層的矽和矽鍺，這種結構稱為「超晶格」。然後用光刻圖案切除超晶格的一部分，留下一個鰭狀結構。超晶格晶體為後續開發過程提供了強大的支撐結構。

接下來在超晶格上放置一塊「假的」多晶矽，保護前者不受下一步操作的影響。這一步驟稱為垂直堆疊的雙源/漏電過程，在頂部奈米帶(未來的NMOS位置)的兩端生長摻磷矽，同時在底部奈米帶(未來的PMOS位置)上選擇性地生長摻硼矽鍺。之後，在電源周圍放置電介質，並透過放電使它們彼此隔離。

3D 堆疊有效地使每平方毫米CMOS 電晶體密度翻倍，實際密度取決於所涉及的邏輯單元的複雜性。

最後是閘的建構。首先移除先前安裝的假門，露出矽奈米帶。接下來只蝕刻掉鍺矽，釋放出一堆平行的矽奈米帶，這就是電晶體的通道區域。

然後在奈米帶的四面塗上一層極薄的絕緣層，這層絕緣層具有很高的介電常數。奈米帶通道是如此之小，無法像平面電晶體那樣有效地以化學方式塗敷。

用金屬環繞底部的奈米帶形成一個 p 摻雜通道，頂部的奈米帶與另一個奈米帶形成一個 n 摻雜通道。這樣，門堆疊建造完成，兩個晶體管安裝完畢。

這個過程可能看起來很複雜，但它比另一種技術( 順序3D堆疊 )要好。如果使用後者，NMOS 元件和 PMOS 元件要安裝在分離的晶片上，然後把兩者合在一起，將PMOS層轉移到 NMOS 晶片上。而自對齊3D堆疊方法加工步驟較少，可以更嚴格的控制製造成本。

更重要的是，這種自對齊方法也避免了在連接兩片晶圓時可能發生的對準錯誤問題。製作所有需要的連接到3D堆疊CMOS 挑戰性很高。電源連接將需要從下面的設備堆疊。在設計上，NMOS 元件[上]和 PMOS 元件[下]有單獨的源/漏接觸，但是兩個元件共用一個閘極。

值得注意的是，需要最佳化NMOS 與PMOS 之間的垂直間距：如果太短，就會增加寄生電容，如果太長，就會增加兩個設備之間互連的電阻。無論哪種極端情況都會導致電路變慢，消耗更多的電力。

#

许多设计研究，如美国 TEL 研究中心在 IEDM 2021会议上提出的一项研究，提出在3D CMOS 有限的空间内提供所有必要的互连，这样做不会显著增加它们构成的逻辑单元的面积。该研究表明，在寻找最佳互连选择方面存在许多创新的机会。

摩尔定律的未来

有了带状场效应晶体管和3D CMOS，我们就有了一条为摩尔定律续命明确路线，至少可以续到2024年以后。

在2005年的一次采访中，摩尔定律的提出者戈登 · 摩尔承认「自己时不时地对取得的进步感到惊讶」。

他说，「一路走来，有好几次我都以为我们已经走到了尽头，结果我们的创意无限工程师们想出了克服困难的办法。」

随着晶体管制造工艺经过 FinFET，并随着不断优化来到RibbonFET时代， 最终向3D堆叠 CMOS工艺的迈进，我们预计，留给戈登·摩尔先生的惊讶不久还会到来的。

以上是電晶體救命稻草來了：3D堆疊CMOS，摩爾定律又續10年？的詳細內容。更多資訊請關注PHP中文網其他相關文章！