回歸元學習,基於變分特徵聚合的少樣本目標檢測實現新SOTA
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB轉載
- 2023-04-12 18:46:03934瀏覽
不同於傳統的目標偵測問題,少樣本目標偵測(FSOD)假設我們有許多的基礎類別樣本,但只有少量的新穎類別樣本。其目標是研究如何將基礎類別的知識遷移到新穎類,進而提升檢測器對新穎類的辨識能力。
FSOD 通常遵循兩階段訓練範式。在第一階段,偵測器使用豐富的基礎類別樣本進行訓練,以學習目標偵測任務所需的通用表示,如目標定位和分類。在第二階段中,檢測器僅使用 少量(如 1, 2, 3...)新穎類樣本進行微調。然而由於基礎類和新穎類樣本數量的不平衡,其學習到的模型通常偏向基礎類,進而導致新穎類目標與相似的基礎類混淆。此外,由於每個新穎類別只有少量樣本,因此模型對新穎類的變異數很敏感。例如,隨機採樣新穎類樣本進行多次訓練,每次的結果都會有較大的差異。因此十分有必要提升模型在少樣本下的穩健性。
近期,騰訊優圖實驗室與武漢大學提出了基於變分特徵聚合的少樣本目標偵測模型 VFA。 VFA 的整體結構是基於改進版的元學習目標檢測框架Meta R-CNN ,並提出了兩種特徵聚合方法:類別無關特徵聚合CAA(Class-Agnostic Aggregation)和變分特徵聚合VFA(Variational Feature Aggregation)。
特徵聚合是 FSOD 中的關鍵設計,其定義了 Query 和 Support 樣本之間的互動方式。前面的方法如 Meta R-CNN 通常採用類別相關特徵聚合 CSA(class-specific aggregation),即同類 Query 和 Support 樣本的特徵進行特徵聚合。與此相反,本文提出的 CAA 允許不同類別樣本之間的特徵聚合。由於 CAA 鼓勵模型學習類別無關的表示,其降低了模型對基礎類別的偏差。此外,不同類別之間的交互作用能夠更好地建模類別間的關係,從而降低了類別的混淆。
基於CAA,本文又提出了VFA,採用變分編碼器(VAEs)將Support 樣本編碼為類別的分佈,並從學習到的分佈中採樣新的Support特徵進行特徵融合。相關工作 [1] 指出類內方差(如外觀的變化)在不同類別之間是相似的,並且可以透過常見的分佈進行建模。因此我們可以利用基礎類別的分佈來估計新穎類別的分佈,進而提高少樣本情況下特徵聚合的穩健性。
VFA 在多個FSOD 資料集上表現優於目前最好的模型,##相關研究已經被AAAI 2023 錄取為Oral。

論文網址:https://arxiv.org/abs/2301.13411
#VFA 模型細節更強的基準方法:Meta R-CNN
目前FSOD 的工作主要可以分為兩類:基於元學習(meta learning)的方法和基於微調(fine-tuning)的方法。早期的一些工作證明元學習對 FSOD 是有效的,但基於微調的方法在最近受到越來越多的關注。 本文首先建立了一個基於元學習的基線方法Meta R-CNN ,縮小了兩種方法之間的差距,在某些指標上甚至超過了基於微調的方法 。
我們首先分析了兩種方法在實作上的一些差距,以元學習方法Meta R-CNN [2] 和基於微調的方法TFA [3] 為例,雖然這兩種方法都遵循兩階段訓練範式,TFA 在微調階段使用額外的技術最佳化模型:
- TFA 凍結了大部分網路參數,只訓練最後的分類和迴歸層,這樣模型就不會過度擬合少樣本類別。
- TFA 不是隨機初始化分類層,而是複製基礎類別的預訓練權重,只初始化新穎類別的權重。
- TFA 採用餘弦分類器(cosine classifier)而不是線性分類器。
考慮到 TFA 的成功,我們建構了 Meta R-CNN 。如下表 1 所示,只要我們仔細處理微調階段,後設學習方法也能達到較好的效果。因此,本文選擇 Meta R-CNN 作為基線方法。
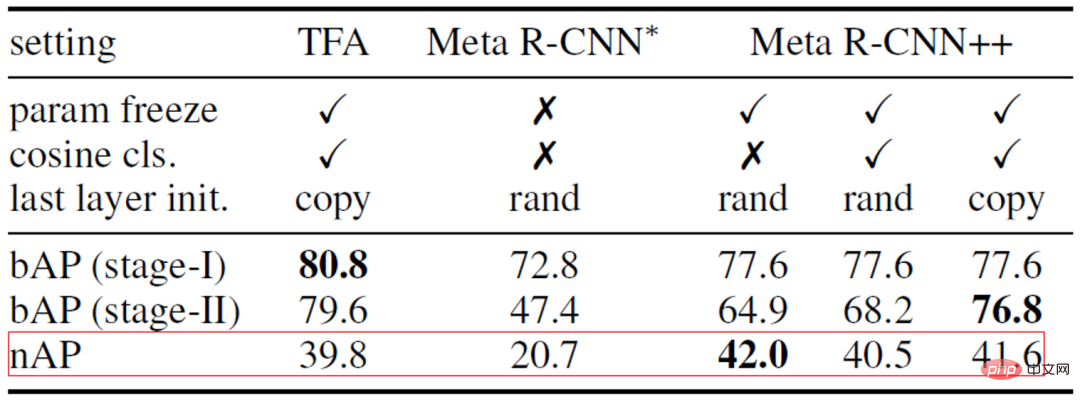
表一:Meta R-CNN 與TFA 的比較與分析
類別無關特徵聚合CAA
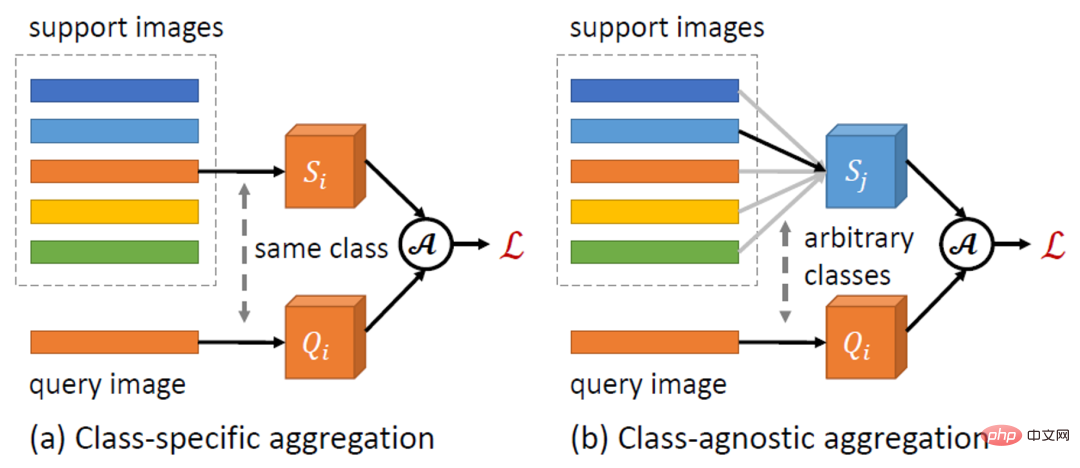
##圖一:類別無關特徵聚合CAA 示意圖
本文提出一個簡單而有效的類別無關特徵聚合方法CAA 。如上圖一所示,CAA 允許不同類別之間的特徵聚合,進而鼓勵模型學習類別無關的表示,從而減少類別間的偏向和類別之間的混淆。具體來說,對於類別
。如上圖一所示,CAA 允許不同類別之間的特徵聚合,進而鼓勵模型學習類別無關的表示,從而減少類別間的偏向和類別之間的混淆。具體來說,對於類別
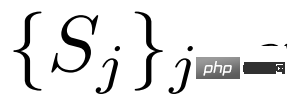 的每個RoI 特徵和一組Support 特徵,
的每個RoI 特徵和一組Support 特徵, 我們隨機選擇一個類別的Support 特徵
我們隨機選擇一個類別的Support 特徵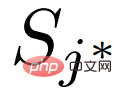 的
的
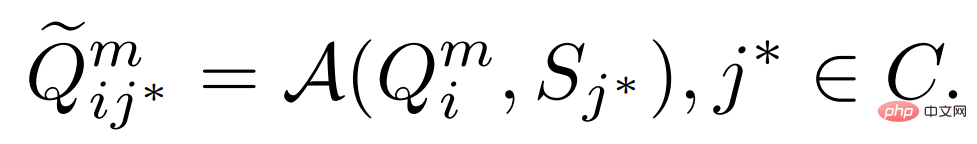
##然後我們將聚合特徵

#提供給偵測子網路

#以輸出分類分數
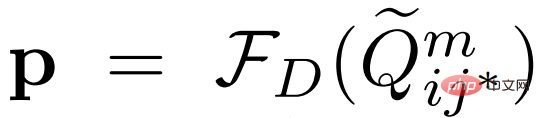 。
。
變分特徵聚合 VFA
####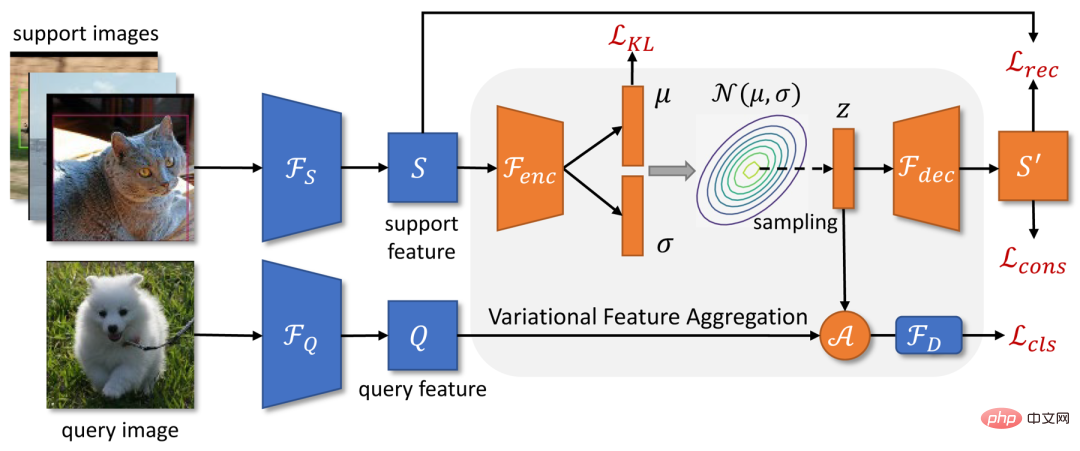
先前的工作通常將Support 樣本編碼為單一特徵向量來表示類別的中心。然而在樣本較少且變異數較大的情況下,我們很難對類中心做出準確的估計。在本文中,我們首先將 Support 特徵轉換為類別的分佈。由於估計出的類別分佈不偏向特定樣本,因此從分佈中採樣的特徵對樣本的變異數有較好的穩健性。 VFA 的框架如上圖二所示。
a)變分特徵學習。 VFA 採用變分自編碼器 VAEs [4] 來學習類別的分佈。如圖二所示,對於一個Support 特徵S,我們首先使用編碼器 來估計分佈的參數
來估計分佈的參數
 # ,接著從分佈
# ,接著從分佈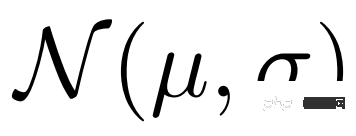 中透過變分推理(variational inference)取樣
中透過變分推理(variational inference)取樣 ,最後透過解碼器
,最後透過解碼器 得到重構的Support 特徵
得到重構的Support 特徵 。在最佳化VAE 時,除了常見的KL Loss
。在最佳化VAE 時,除了常見的KL Loss 和重構Loss
和重構Loss ,本文也使用了一致性Loss 使得學習到的分佈保留類別資訊:
,本文也使用了一致性Loss 使得學習到的分佈保留類別資訊:
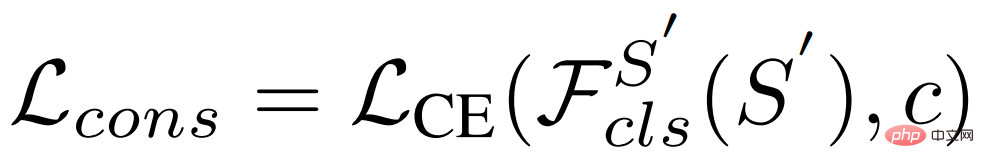
b)變分特徵融合。由於 Support 特徵被轉換為類別的分佈,我們可以從分佈中取樣特徵並與 Query 特徵聚合。具體來說,VFA 同樣採用類別無關聚合 CAA,但將 Query 特徵 與變異特徵
與變異特徵 聚合在一起。給定類別
聚合在一起。給定類別 的Query 特徵
的Query 特徵 和類別
和類別 的Support 特徵
的Support 特徵
,我們首先估計其分佈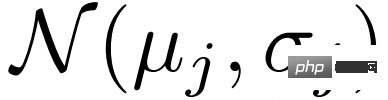 #,並取樣變分特徵
#,並取樣變分特徵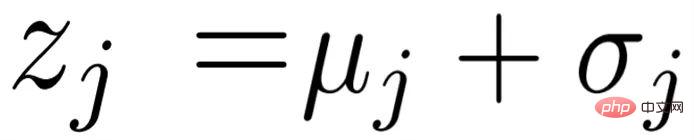 ;然後透過下面的公式將其融合在一起:
;然後透過下面的公式將其融合在一起:
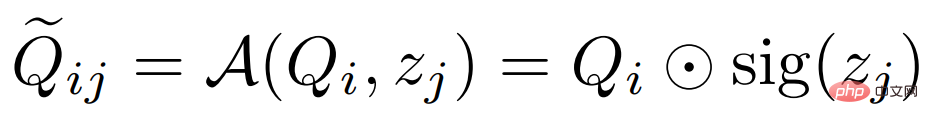
其中 表示通道乘法,而sig 是sigmoid 運算的縮寫。在訓練階段,我們隨機選擇一個Support 特徵
表示通道乘法,而sig 是sigmoid 運算的縮寫。在訓練階段,我們隨機選擇一個Support 特徵 進行聚合;在測試階段,我們對
進行聚合;在測試階段,我們對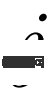
類別的 ##個Support 特徵取平均值
##個Support 特徵取平均值 ,並估計分佈
,並估計分佈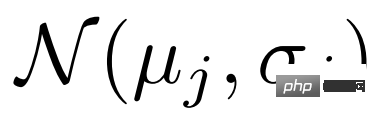
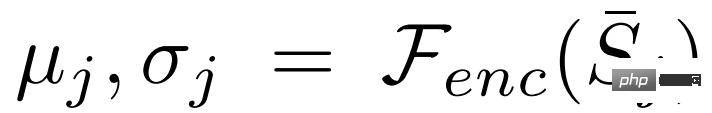 。
。
分類 - 回歸任務解耦
#通常情況下,偵測子網路 包含一個共享特徵擷取器
包含一個共享特徵擷取器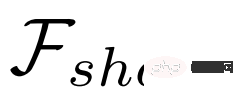 和兩個獨立的網路:分類子網絡
和兩個獨立的網路:分類子網絡 和回歸子網路
和回歸子網路 。在前面的工作中,聚合後的特徵被輸入到偵測子網路中進行目標分類和邊界框回歸。但是分類任務需要平移不變特徵,而迴歸需要平移協變的特徵。由於 Support 特徵表示的是類別的中心,具有平移不變性,因此聚合後特徵會損害迴歸任務。
。在前面的工作中,聚合後的特徵被輸入到偵測子網路中進行目標分類和邊界框回歸。但是分類任務需要平移不變特徵,而迴歸需要平移協變的特徵。由於 Support 特徵表示的是類別的中心,具有平移不變性,因此聚合後特徵會損害迴歸任務。
本文提出一個簡單的分類 - 回歸任務解耦。讓 和
和 表示原始和聚合後的Query 特徵,先前的方法對這兩個任務都採用
表示原始和聚合後的Query 特徵,先前的方法對這兩個任務都採用 ,其中分類分數
,其中分類分數 與預測邊界框
與預測邊界框 定義為:
定義為:
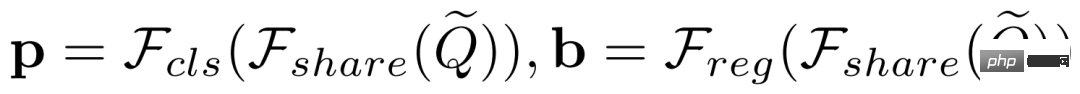
為了解耦這些任務,我們採用單獨的特徵提取器並使用原始的Support 特徵 進行邊界框回歸:
進行邊界框回歸:
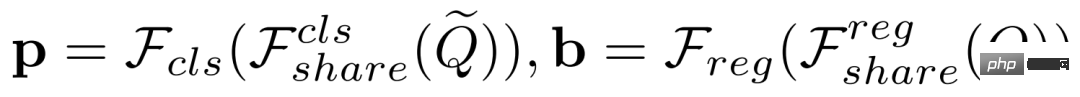
我們所採用的資料集:PASCAL VOC、 MS COCO。 評估指標:新穎類別平均精確度 nAP、基礎類別平均精確度 bAP。
主要結果
#VFA 在兩個資料集上都取得了較好的結果。如在 PASCAL VOC 資料集上(下表二),VFA 顯著高於先前的方法;VFA 的 1-shot 結果甚至高於一些方法 10-shot 的結果。
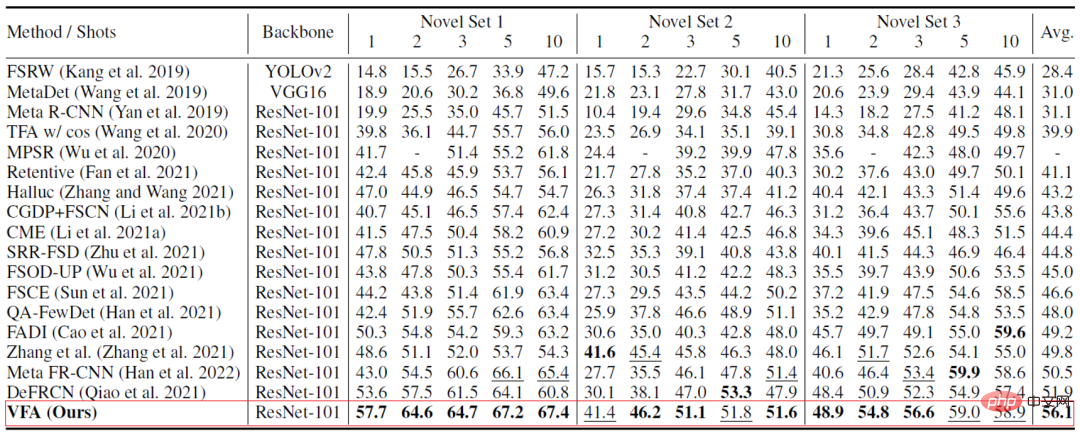
消融實驗
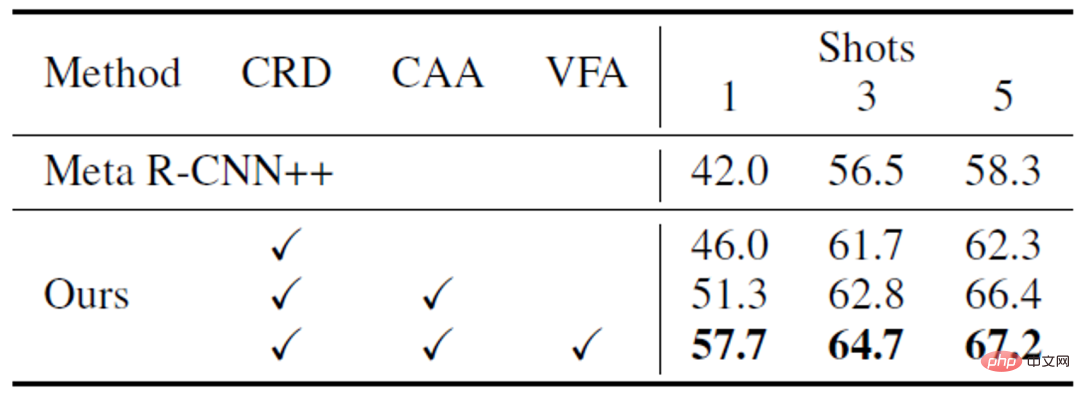
a)不同模組的作用 。如下表三所示,VFA 的不同模組可以共同作用,提升模型的表現。
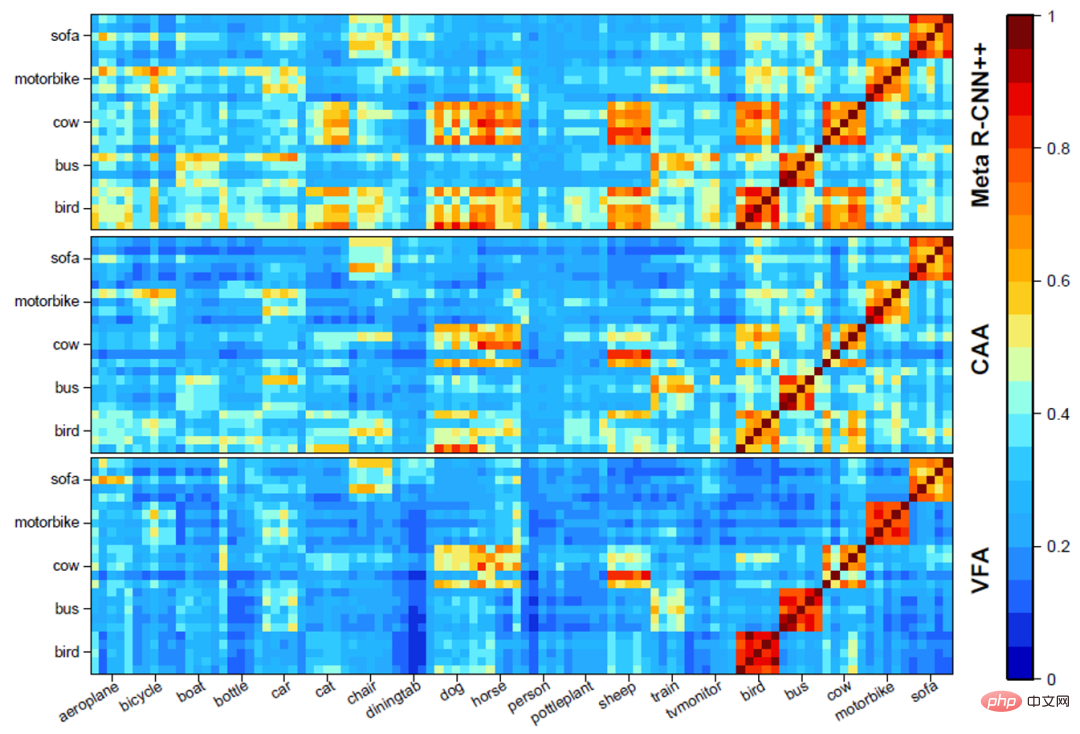
b) 不同特徵聚合方法視覺化分析。如下圖三所示,CAA 可以減少基礎類與新穎類之間的混淆;VFA 在 CAA 的基礎上,進一步增強了類間的區分度。
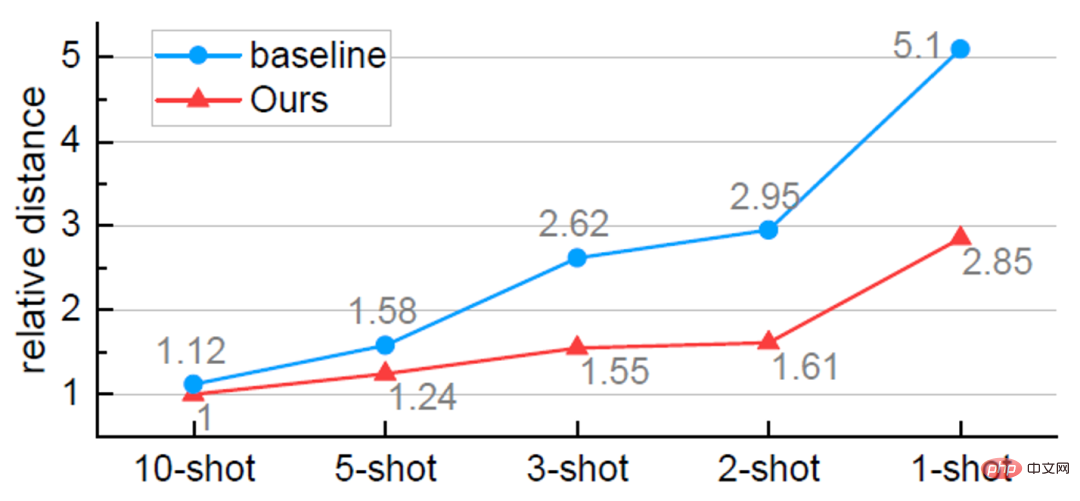
c)更準確的類別中心點估計值。如下圖四所示,VFA 可以更準確的估計出類別的中心。且隨著樣本數的減少,估計的準確度逐漸高於基線方法。這也解釋了為什麼我們的方法在樣本少的情況下(K=1)表現的更好。
d)結果視覺化。

結論
本文回歸了基於元學習的FSOD 中特徵聚合方法,並提出了類別無關特徵聚合CAA 和變異特徵聚合VFA。 CAA 可以減少基礎類別和新穎類別之間的類別偏差和混淆;VFA 將樣本轉換為類別分佈以實現更穩健的特徵聚合。本文提出的方法在 PASCAL VOC 和 MS COCO 資料集上的實驗證明了其有效性。
以上是回歸元學習,基於變分特徵聚合的少樣本目標檢測實現新SOTA的詳細內容。更多資訊請關注PHP中文網其他相關文章!

