本綜述(Diffusion Models: A Comprehensive Survey of Methods and Applications)來自加州大學& Google Research 的Ming-Hsuan Yang、北京大學崔斌實驗室以及CMU、UCLA、蒙特利爾Mila 研究院等眾研究團隊,首次對現有的擴散生成模型(diffusion model)進行了全面的總結分析,從diffusion model 算法細化分類、和其他五大生成模型的關聯以及在七大領域中的應用等方面展開,最後提出了diffusion model 的現有limitation 和未來的發展方向。

文章連結:https://arxiv.org/abs/2209.00796論文分類總結github 連結: https://github.com/YangLing0818/Diffusion-Models-Papers-Survey-Taxonomy
##介紹擴散模型(diffusion models)是深度生成模型中新的SOTA。擴散模型在圖片生成任務中超越了原始SOTA:GAN,並且在許多應用領域都有出色的表現,如計算機視覺,NLP、波形信號處理、多模態建模、分子圖建模、時間序列建模、對抗性淨化等。此外,擴散模型與其他研究領域有著密切的聯繫,如穩健學習、表示學習、強化學習。然而,原始的擴散模型也有缺點,它的採樣速度慢,通常需要數千個評估步驟才能抽取一個樣本;它的最大似然估計無法和基於似然的模型相比;它泛化到各種數據類型的能力較差。如今許多研究已經從實際應用的角度解決上述限製做出了許多努力,或從理論角度對模型能力進行了分析。
然而,現在缺乏對擴散模型從演算法到應用的最新進展的系統性回顧。為了反映這一快速發展領域的進展,我們對擴散模型進行了首個全面綜述。我們設想我們的工作將闡明擴散模型的設計考慮和先進方法,展示其在不同領域的應用,並指出未來的研究方向。此綜述的摘要如下圖所示:

#儘管diffusion model 在各類別任務中都有著優秀的表現,它仍有自己的缺點,並有許多研究對diffusion model 進行了改善。為了有系統地闡明diffusion model 的研究進展,我們總結了原始擴散模型的三個主要缺點,採樣速度慢,最大化似然差、數據泛化能力弱,並提出將的diffusion models 改進研究分為對應的三類:取樣速度提升、最大似然增強和資料泛化增強。我們首先說明改善的動機,再根據方法的特性將每個改進方向的研究進一步細化分類,從而清楚的展現方法之間的聯繫與區別。在此我們僅選取部分重要方法為例, 我們的工作中對每類方法都做了詳細的介紹,內容如圖所示:

在分析完三類擴散模型後,我們將介紹其他的五種生成模型GAN,VAE,Autoregressive model, Normalizing flow, Energy-based model。考慮到擴散模型的優良性質,研究者們已經根據其特性將diffusion model 與其他生成模型結合,所以為了進一步展現diffusion model 的特點和改進工作,我們詳細地介紹了diffusion model 和其他生成模型的結合的工作並闡明了在原始生成模型上的改進之處。 Diffusion model 在許多領域都有優異的表現,並且考慮到不同領域的應用中diffusion model 產生了不同的變形,我們系統地介紹了diffusion model 的應用研究,其中包含如下領域:計算機視覺,NLP、波形信號處理、多模態建模、分子圖建模、時間序列建模、對抗性淨化。
對於每個任務,我們定義了該任務並介紹利用擴散模型處理任務的工作,我們將本項工作的主要貢獻總結如下:
- 新的分類方法#:我們對擴散模型和其應用提出了一種新的、系統的分類法。具體的我們將模型分為三類:取樣速度增強、最大似然估計增強、資料泛化增強。進一步地,我們將擴散模型的應用分為七類:電腦視覺,NLP、波形訊號處理、多模態建模、分子圖建模、時間序列建模、對抗性淨化。
- 全面的回顧:我們首次全面地概述了現代擴散模型及其應用。我們展示了每種擴散模型的主要改進,和原始模型進行了必要的比較,並總結了相應的論文。對於擴散模型的每種類型的應用,我們展示了擴散模型要解決的主要問題,並說明它們如何解決這些問題。
- 未來研究方向#:我們對未來研究提出了開放型問題,並對擴散模型在演算法和應用方面的未來發展提供了一些建議。
擴散模型基礎
生成式建模的一個核心問題是模型的靈活性和可計算性之間的權衡。擴散模型的基本概念是正向擴散過程來系統地擾動資料中的分佈,然後透過學習反向擴散過程來恢復資料的分佈,這樣就了產生一個高度靈活且易於計算的生成模型。
A.Denoising Diffusion Probabilistic Models(DDPM)
一個DDPM 由兩個參數化馬可夫鏈組成,並使用變異推論以在有限時間後產生與原始資料分佈一致的樣本。前向鏈的作用是擾動數據,它根據預先設計的噪聲進度向數據逐漸加入高斯噪聲,直到數據的分佈趨於先驗分佈,即標準高斯分佈。反向鏈從給定的先驗開始並使用參數化的高斯轉換核,學習逐步恢復原始資料分佈。以 表示原始資料及其分佈, 則前向鏈的分佈是可由下式表示:
表示原始資料及其分佈, 則前向鏈的分佈是可由下式表示:

##這說明前向鍊是馬可夫過程,x_t 是加入t 步雜訊後的樣本,β_t 是事先給定的控制雜訊進度的參數。當 趨於 1 時,x_T 可以近似地認為服從標準高斯分佈。當β_t 很小時,逆向過程的轉移核可以近似認為也是高斯的:
趨於 1 時,x_T 可以近似地認為服從標準高斯分佈。當β_t 很小時,逆向過程的轉移核可以近似認為也是高斯的:

我們可以將變分下界作為損失函數來學習:

B.Score-Based Generative Models(SGM)
##上述DDPM 可視為SGM 的離散形式。 SGM 建構一個隨機微分方程式(SDE)來平滑的擾亂資料分佈,將原始資料分佈轉換到已知的先驗分佈:
 ##和一個對應的逆向SDE,來將先驗分佈變換回原始資料分佈:
##和一個對應的逆向SDE,來將先驗分佈變換回原始資料分佈:
因此,要逆轉擴散過程並產生數據,我們需要的唯一資訊就是在每個時間點的分數函數。利用score-matching 的技巧我們可以透過以下損失函數來學習分數函數:

#對兩種方法的進一步介紹和兩者關係的介紹請參考我們的文章。
原始擴散模型的三個主要缺點,取樣速度慢,最大化似然差、資料泛化能力弱。最近許多研究都在解決這些缺點,因此我們將改進的擴散模型分為三類:採樣速度提升、最大似然增強和資料泛化增強。在接下來的三、四、五節我們將對這三類模型進行詳細的介紹。
取樣加速方法
在應用時,為了讓新樣本的品質達到最佳,擴散模型往往需要進行成千上萬步驟計算來取得一個新樣本。這限制了 diffusion model 的實際應用價值,因為在實際應用時,我們往往需要產生大量的新樣本,來為下一步處理提供材料。研究者在提高 diffusion model 採樣速度上進行了大量的研究。我們對這些研究進行了詳細的闡述。我們將其細化分類為三種方法:Discretization Optimization,Non-Markovian Process,Partial Sampling。
A.Discretization Optimization 方法最佳化求解 diffusion SDE 的方法。因為現實中求解複雜 SDE 只能使用離散解來逼近真正的解,所以該類別方法試圖優化 SDE 的離散化方法,在保證樣本品質的同時減少離散步數。 SGM 提出了一個通用的方法來求解逆向過程,即對前向和後向過程採取相同的離散方法。如果給定了前向SDE 的離散方式:

#那麼我們就可以以相同的方式離散化逆向SDE:

這種方法比樸素DDPM 效果略好一點。進一步,SGM 在 SDE 解算器中加入了一個矯正器,讓每一步產生的樣本都有正確的分佈。在求解的每一步,求解器給出一個樣本後,矯正器都使用馬可夫鏈蒙特卡羅方法來矯正剛產生的樣本的分佈。實驗顯示向求解器中加入矯正器比直接增加求解器的步數效率更高。
B.Non-Markovian Process 方法突破了原有Markovian Process 的限制,其逆過程的每一步可以依賴更多以往的樣本來進行預測新樣本,所以在步長較大時也能做出較好的預測,加速取樣過程。其中主要的工作DDIM,不再假設前向過程是馬可夫過程,而是服從如下分佈:

#DDIM 的取樣過程可以視為離散化的神經常微分方程,其取樣過程更有效率,並且支持樣本的內插。進一步的研究發現 DDIM 可以視為流形上擴散模型 PNDM 的特殊情況。
C.Partial Sampling 方法透過在generation process 中忽略一部分的時間節點,而只使用剩下的時間節點來產生樣本,直接減少了取樣時間。例如,Progressive Distillation 從訓練好的擴散模型中蒸餾出效率更高的擴散模型。對於訓練好的一個擴散模型,Progressive Distillation 會從新訓練一個擴散模型,使新的擴散模型的一步對應於訓練好的擴散模型的兩步,這樣新模型就可以省去舊模型一半的採樣過程。具體演算法如下:

不斷循環這個蒸餾過程就能讓取樣步驟指數級下降。
最大似然估計加強
擴散模型在最大似然估計的表現差於基於似然函數的生成模型,但最大化似然估計在諸多應用場景都有重要意義,例如圖片壓縮, 半監督學習, 對抗性淨化。由於對數似然難以直接計算,研究主要集中在最佳化和分析變分下界(VLB)。我們對提高擴散模型最大似然估計的模型進行了詳細的闡述。我們將其細化分類為三類方法:Objectives Designing,Noise Schedule Optimization,Learnable Reverse Variance。
A.Objectives Designing 方法利用擴散SDE 推倒出生成資料的對數似然與分數函數匹配的損失函數的關係。這樣透過適當設計損失函數,就可以最大化 VLB 和對數似然。 Song et al. 證明了可以設計損失函數的權重函數,使得 plug-in reverse SDE 產生樣本的似然函數值小於等於損失函數值,即損失函數是似然函數的上界。分數函數擬合的損失函數如下:

我們只要將權重函數λ(t)設為擴散係數g(t)即可讓損失函數成為似然函數的VLB,即:

B.Noise Schedule Optimization 透過設計或學習前向過程的雜訊進度來增加VLB。 VDM 證明了當離散步數接近無窮時,損失函數完全由信噪比函數SNR(t)的端點決定:

##那麼在離散步數接近無窮時,可以透過學習信噪比函數SNR(t)的端點最優化VLB,而透過學習信噪比函數中間部分的函數值來實現模型其他方面的改進。
C.Learnable Reverse Variance 方法學習反向過程的方差,從而較少擬合誤差,可以有效地最大化VLB 。 Analytic-DPM 證明,在DDPM 和DDIM 中存在反向過程中的最優期望和方差:

使用上述公式和訓練好的分數函數,在給定前向過程的條件下,最優的VLB 可以近似達到。
資料泛化增強擴散模型假設資料存在於歐幾里德空間,即具有平面幾何形狀的流形,並添加高斯雜訊將不可避免地將資料轉換為連續狀態空間,所以擴散模型最初只能處理圖片等連續性數據,直接應用離散資料或其他資料類型的效果較差。這限制了擴散模型的應用場景。數個研究工作將擴散模型推廣到適用於其他資料類型的模型,我們對這些方法進行了詳細地解釋。我們將其細化分類為兩類方法:Feature Space Unification,Data-Dependent Transition Kernels。
A.Feature Space Unification# 方法將資料轉換為統一形式的latent space,然後再latent space上進行擴散。 LSGM 提出將資料經由 VAE 框架先轉換到連續的 latent space 上後再在其上進行擴散。這個方法的困難在於如何同時訓練 VAE 和擴散模型。 LSGM 顯示由於潛在先驗是 intractable 的,因此分數匹配損失不再適用。 LSGM 直接使用 VAE 中傳統的損失函數 ELBO 作為損失函數,並導出了 ELBO 和分數匹配的關係:

該式在忽略常數的意義下成立。透過參數化擴散過程中樣本的分數函數,LSGM 可以高效率的學習和最佳化 ELBO。
B.Data-Dependent Transition Kernels 方法根據資料類型的特性設計diffusion process 中的transition kernels ,使擴散模型可以直接應用於特定的資料類型。 D3PM 為離散型資料設計了 transition kernel,可以設為 lazy random-walk,absorbing state 等。 GEODIFF 為 3D 分子圖資料設計了平移 - 旋轉不變的圖神經網絡,並且證明了具有不變性的初始分佈和 transition kernel 可以導出具有不變性的邊緣分佈。假設T 是平移- 旋轉變換,如:

#那麼產生的樣本分佈也有平移- 旋轉不變性:

和其他生成模型的連結在下面的每個小節中,我們首先介紹其他五類重要的生成模型,並分析它們的優點和局限性。然後我們介紹了擴散模型是如何與它們聯繫起來的,並說明透過結合擴散模型來改進這些生成模型。 VAE,GAN,Autoregressive model, Normalizing flow, Energy-based model 和擴散模型的聯繫如下圖所示:

- DDPM 可以視為層次馬可夫VAE(hierarchical Markovian VAE)。但 DDPM 和一般的 VAE 也有差別。 DDPM 作為 VAE,它的 encoder 和 decoder 都服從高斯分佈、有馬爾科夫行;其隱變量的維數和資料維數相同;decoder 的所有層都共用一個神經網路。
- DDPM 可以幫助 GAN 解決訓練不穩定的問題。因為資料是在高維空間中的低維流形中,所以 GAN 產生資料的分佈和真實資料的分佈重合度低,導致訓練不穩定。擴散模型提供了一個系統地增加噪音的過程,透過擴散模型為生成的資料和真實資料添加噪音,然後將加入噪音的資料送入判別器,這樣可以高效地解決GAN 無法訓練、訓練不穩定的問題。
- Normalizing flow 透過雙射函數將資料轉換到先驗分佈,這樣的作法限制了 Normalizing flow 的表達能力,導致應用效果較差。類比擴散模型在 encoder 中加入噪聲,可以增加 Normalizing flow 的表達能力,而從另一個視角來看,這樣的做法是將擴散模型推廣到前向過程也可學習的模型。
- Autoregressive model 在需要保證資料有一定的結構,這導致設計和參數化自迴歸模型非常困難。擴散模型的訓練啟發了自回歸模型的訓練,透過特定的訓練方式避免了設計的困難。
- Energy-based model 直接對原始資料的分佈建模,但直接建模導致學習和取樣都比較困難。透過使用擴散恢復似然,模型可以先對樣本加入微小的噪聲,再從有略微噪聲的樣本分佈來推斷原始樣本的分佈,使的學習和採樣過程更簡單和穩定。
擴散模型的應用
在本節中,我們分別介紹了擴散模型在電腦視覺、自然語言處理、波形訊號處理、多模態學習、分子圖生成、時間序列以及對抗學習等七大應用方向中的應用,並對每類應用中的方法進行了細分並解析。例如在電腦視覺中可以用 diffusion model 進行影像補全修復(RePaint):

在多模態任務中可以用diffusion model 進行文字到圖像的生成(GLIDE):

還可以在分子圖生成中以diffusion model 進行藥物分子與蛋白質分子的生成(GeoDiff):

應用分類總表見表:

未來研究方向
- 應用假設再檢驗。我們需要檢視我們在應用中普遍接受的假設。例如,實務上普遍認為擴散模型的前向過程會將資料轉換為標準高斯分佈,但事實並非如此,更多的前向擴散步驟會使最終的樣本分佈與標準高斯分佈更接近,與取樣過程一致;但更多的前向擴散步驟也會使估計分數函數更加困難。理論的條件很難獲得,因此在實務中操作中會導致理論和實務的不匹配。我們應該意識到這種情況並設計適當的擴散模型。
- 從離散時間到連續時間。由於擴散模型的靈活性,許多經驗方法可以透過進一步分析來加強。透過將離散時間的模型轉換到對應的連續時間模型,然後再設計更多、更好的離散方法,這樣的研究想法有前景。
- 新的生成過程。擴散模型透過兩種主要方法產生樣本:一是離散化反向擴散 SDE,然後透過離散的反向 SDE 產生樣本;另一個是使用逆過程中馬可夫性質逐步去雜訊樣本。然而,對於某些任務,在實務上很難應用這些方法來產生樣本。因此,需要進一步研究新的生成過程和觀點。
- 泛化到更複雜的場景和更多的研究領域。雖然目前 diffusion model 已經應用到多個場景中,但是大多數局限於單輸入單輸出的場景,將來可以考慮將其應用到更複雜的場景,例如 text-to-audiovisual speech synthesis。也可以考慮和更多的研究領域結合。
以上是擴散模型爆火,這是首篇綜述與Github論文分類總結的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 讓我們跳舞:結構化運動以微調我們的人類神經網Apr 27, 2025 am 11:09 AM
讓我們跳舞:結構化運動以微調我們的人類神經網Apr 27, 2025 am 11:09 AM科學家已經廣泛研究了人類和更簡單的神經網絡(如秀麗隱桿線蟲中的神經網絡),以了解其功能。 但是,出現了一個關鍵問題:我們如何使自己的神經網絡與新穎的AI一起有效地工作
 新的Google洩漏揭示了雙子AI的訂閱更改Apr 27, 2025 am 11:08 AM
新的Google洩漏揭示了雙子AI的訂閱更改Apr 27, 2025 am 11:08 AMGoogle的雙子座高級:新的訂閱層即將到來 目前,訪問Gemini Advanced需要$ 19.99/月Google One AI高級計劃。 但是,Android Authority報告暗示了即將發生的變化。 最新的Google P中的代碼
 數據分析加速度如何求解AI的隱藏瓶頸Apr 27, 2025 am 11:07 AM
數據分析加速度如何求解AI的隱藏瓶頸Apr 27, 2025 am 11:07 AM儘管圍繞高級AI功能炒作,但企業AI部署中潛伏的巨大挑戰:數據處理瓶頸。首席執行官慶祝AI的進步時,工程師努力應對緩慢的查詢時間,管道超載,一個
 Markitdown MCP可以將任何文檔轉換為Markdowns!Apr 27, 2025 am 09:47 AM
Markitdown MCP可以將任何文檔轉換為Markdowns!Apr 27, 2025 am 09:47 AM處理文檔不再只是在您的AI項目中打開文件,而是將混亂變成清晰度。諸如PDF,PowerPoints和Word之類的文檔以各種形狀和大小淹沒了我們的工作流程。檢索結構化
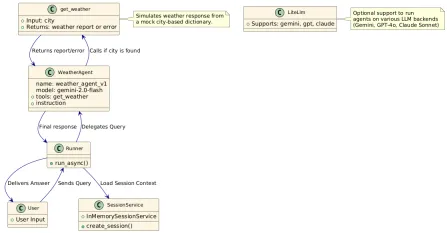 如何使用Google ADK進行建築代理? - 分析VidhyaApr 27, 2025 am 09:42 AM
如何使用Google ADK進行建築代理? - 分析VidhyaApr 27, 2025 am 09:42 AM利用Google的代理開發套件(ADK)的力量創建具有現實世界功能的智能代理!該教程通過使用ADK來構建對話代理,並支持Gemini和GPT等各種語言模型。 w
 在LLM上使用SLM進行有效解決問題-Analytics VidhyaApr 27, 2025 am 09:27 AM
在LLM上使用SLM進行有效解決問題-Analytics VidhyaApr 27, 2025 am 09:27 AM摘要: 小型語言模型 (SLM) 專為效率而設計。在資源匱乏、實時性和隱私敏感的環境中,它們比大型語言模型 (LLM) 更勝一籌。 最適合專注型任務,尤其是在領域特異性、控制性和可解釋性比通用知識或創造力更重要的情況下。 SLM 並非 LLMs 的替代品,但在精度、速度和成本效益至關重要時,它們是理想之選。 技術幫助我們用更少的資源取得更多成就。它一直是推動者,而非驅動者。從蒸汽機時代到互聯網泡沫時期,技術的威力在於它幫助我們解決問題的程度。人工智能 (AI) 以及最近的生成式 AI 也不例
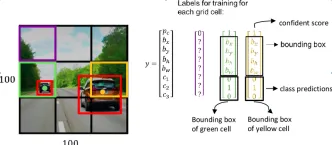 如何將Google Gemini模型用於計算機視覺任務? - 分析VidhyaApr 27, 2025 am 09:26 AM
如何將Google Gemini模型用於計算機視覺任務? - 分析VidhyaApr 27, 2025 am 09:26 AM利用Google雙子座的力量用於計算機視覺:綜合指南 領先的AI聊天機器人Google Gemini擴展了其功能,超越了對話,以涵蓋強大的計算機視覺功能。 本指南詳細說明瞭如何利用
 Gemini 2.0 Flash vs O4-Mini:Google可以比OpenAI更好嗎?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini:Google可以比OpenAI更好嗎?Apr 27, 2025 am 09:20 AM2025年的AI景觀正在充滿活力,而Google的Gemini 2.0 Flash和Openai的O4-Mini的到來。 這些尖端的車型分開了幾週,具有可比的高級功能和令人印象深刻的基準分數。這個深入的比較


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

Atom編輯器mac版下載
最受歡迎的的開源編輯器

Dreamweaver CS6
視覺化網頁開發工具

EditPlus 中文破解版
體積小,語法高亮,不支援程式碼提示功能

Dreamweaver Mac版
視覺化網頁開發工具

SublimeText3 英文版
推薦:為Win版本,支援程式碼提示!






