
導讀:因果推論是資料科學的一個重要分支,在互聯網和工業界的產品迭代、演算法和激勵策略的評估中都扮演者很重要的角色,結合資料、實驗或統計計量模型來計算新的改變所帶來的效益,是決策的基礎。然而,因果推論並不是一件簡單的事。首先,在日常生活中,人們常常把相關和因果混為一談。相關往往代表兩個變數具有同時成長或降低的趨勢,但是因果意味著我們想要知道對一個變數施加改變的時候會發生什麼樣的結果,或者說我們期望得到反事實的結果,如果過去做了不一樣的動作,未來是否會改變?然而困難在於,反事實的數據往往是真實世界中難以觀察和收集的。
本文回顧因果推論的兩個流派-潛在結果模型Rubin Causal Model (RCM; Rubin 1978) 和結構因果模型Causal Diagram (Pearl 1995 )的主要技術思想和方法,以及近年來的新方法和應用。筆者由於學術背景和計量經濟學較為相關,所以引用的方法和論文主要參考了經濟學的文獻,可能在一些方法的理論和應用上的深度與廣度上有所疏漏,請讀者諒解。
潛在結果模型
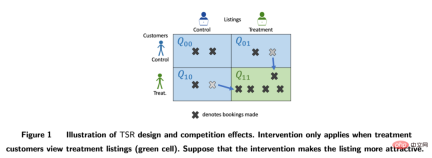
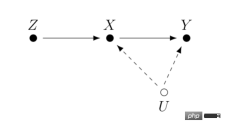
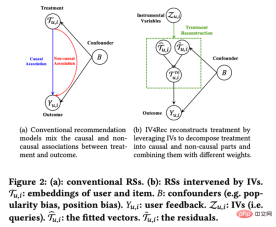
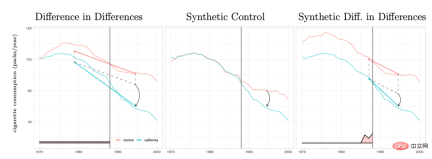
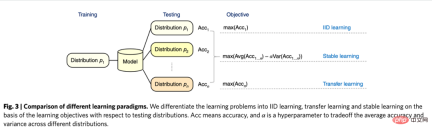
我們把每個研究對像或使用者用i來表示,他們可能會受到一定的策略幹預:Ti=1#代表受到了乾預(實驗組),Ti=0代表沒有受到干預(基準組),對應的我們關心的結果分別是Yi0 和Yi1,但是只有一種情況會真實發生,也就是說Yi0和Yi1只能觀察到其中一個,另一個未知。這裡我們預期得到的因果推論結果是平均處理效果ATE=E[Y1-Y##0##]。 # 我們可以用一定的數學推導來解釋估計ATE的困難之處。由於我們只會觀察到Yi0和Yi1中的一個,我們能夠直接計算的其實是實驗組和基準組之間的組間差異E[Y#i1|Ti=1]-E[Yi0|T##i =0],這個差值進一步可以拆解等於E[Yi1|Ti=1]-E[Yi0#|Ti=1] E[Yi0|T i=1]-E[Y#i0|Ti=0]。其中E[Yi1|T#i=1]-E[ Yi0|T#i=1]是實驗組個體上的平均處理效應(ATT),ATT和ATE往往不相等,這兩者的差異代表我們計算的外在效度(External Validity)。如果樣本限制在某個年齡層的用戶,那麼結果不一定能夠推廣到全年齡層的用戶上,表示我們的分析不一定具備外在效度。上面公式裡的第二部分E[Yi0|Ti =1]-E[Yi0|Ti=0]代表了樣本的選擇性偏差。選擇性偏差在實際生活中常常可能不是0,例如如果實驗組和基準組不是隨機抽樣而來,會在一定的特徵分佈上有差異,那麼就可能會造成選擇性偏差。因此,我們計算的組間差異其實是只有當消除選擇性偏差、具備外在效度,並且基於大量充足的樣本的時候,才代表著我們期望得到的平均處理效應。潛在效果模型的思想方法其實就是透過一定的設定和模型達到這樣的條件。其思想背後,還有比較嚴格的數學假設。以下我們依照不同方法,分別回顧其主要想法與近年來的技術發展與應用,受篇幅限制,斷點迴歸方法這裡就沒有展開做詳細介紹了。 #潛在效果模型最常見的方法就是隨機實驗,或者說是我們在工業界中常用到的A/B測試。我們透過一定的隨機性抽樣來建構實驗組和基準組,來觀察組間的差異。但要指出的是,即便滿足了隨機性,這裡因果推論的有效性還需要滿足一個重要的假設—Stable Unit Treatment Value Assumption (SUTVA)。每個個體的潛在結果只和他自己有關,與其他個體是否被實驗策略幹預無關,同時我們所關心的單一策略幹預沒有不同形式或強度來導致不同的潛在結果。在現實生活中SUTVA假設違背的場景中有很多,也激發了各種新型A/B測試技術手段的發展,例如針對擠佔問題的預算或者策略控制,亦或者是分流設計的改進。我們在這裡舉一些分流相關的例子: 在LinkedIn,實驗人員採用網路抽樣的實驗方法來應對社交網路對於傳統個體隨機試驗的挑戰。首先將使用者分成不同的cluster,每個cluster作為一個個體來隨機分流和計算實驗指標,透過估計使用者的網路效應exposure來修正估計的處理效應(Gui et al. 2015)。 在Airbnb等平台,買家和賣家之間常常存在著相互影響,也會幹擾傳統的實驗方法。研究者透過雙邊實驗設計和庫存的動態模型來建構實驗評估指標(Johari et al. 2022)。需要指出的是,雙邊實驗是個比較嶄新的領域,其實驗設計可以幫助實驗者發現傳統單邊實驗的溢出效應,但是對於實驗結果如何做統計推斷和修正是比較困難並且不一定有絕對答案的,要多結合業務場景來探討。 圖片來自論文Johari et al. (2022) 工具變數是解決線性迴歸問題內生性的一種方法。接下來我們介紹內生性問題和如何透過工具變數解決內生性。內生性的主要問題是如果我們關心X對Y的影響,但是有無法測量的變數U,且U會同時影響X和Y。則X具有內生性,U即上文提到的混淆變數。如果我們能找到一個跟X有關的變數Z,且Z與U不相關。那我們可以透過Z作為工具變數來估計X對Y的因果效應,具體計算方法一般是兩階段最小平方法。工具變數法在實際使用的時候,要注意避免「弱工具變數」的問題,也就是工具變數Z和關心的變數X相關度很低,這樣會造成估計的因果效應有偏差,可以依賴統計檢定方法來確認這樣的問題是否存在。 工具變數法的一個發展是和深度學習模型結合,例如Hartford et al. (2017) 提出的Deep IV方法。這項研究將傳統工具變數的兩階段最小平方法轉換成更靈活的兩個深度神經網路的預測任務,放鬆了傳統方法中對於資料生成過程(DGP)的強假設。 在實際的應用中,基於網路大量A/B測試累積的場景,我們可以透過實驗的meta-learning和工具變數法來學習指標間的因果關係。例如Peysakhovich & Eckles (2018) 利用Facebook的數據,將實驗組資訊作為工具變量,在兩階段最小二乘法的基礎上結合L0正則化,可以解決傳統工具變量法在有限樣本上的bias問題,也能克服現實情境中大量實驗觀察到的效果絕對值比較低(「弱工具變數」)的問題。 工具變數的想法除了學習指標間的影響關係外也可以用來解決推薦系統中的偏差問題。在推薦系統中,模型的訓練往往依賴使用者的歷史觀看和轉評讚的回饋行為,但是這些歷史資料往往被展示的位置、曝光的模式等混淆因素所影響,快手和人大的研究者Si et al . (2022)利用工具變數的想法提出IV4Rec框架,將搜尋的query作為工具變數來分解推薦系統embedding中的因果和非因果關係,和深度學習相結合,在快手資料和公開資料集MIND上都能驗證提升推薦模型的效果。 圖片來自論文Si et al. (2022) #(Matching)是一種被業務廣泛使用的因果分析方法,主要是為了解決當實驗組和控制組由於某種原因(confounder)不可比的時候,透過給實驗組的每一個用戶匹配和他在某些特徵上最相似(CEM粗粒度匹配)或者接受干預概率(propensity score )最相似(PSM傾向性分數配對)的控制組用戶,重新製造可比較的實驗組和控制組。配對是最近似AB/RCT(randomized controlled trial)隨機實驗的方法,操作方法比較類似,結果很直觀。並且,配對是一種非參數估計處理效應的方法,不受制於一般的線性參數模型假設。透過配對之後的樣本,也可以搭配雙重差分的方法,常用於解決新功能滲透率較低的問題。近年來,配對法的發展主要是結合機器學習模型將傾向性分數配對做得更加精準,同時這裡的想法也應用到了一些其他因果方法、機器學習模型的糾偏中,相關內容後文講到的時候會涉及。 近年來,圍繞著面板資料的因果推論有著比較多的新方法來出現。我們先回顧傳統的面板資料方法。 最常用的是雙重差分的方法。最簡單的雙重差分是控制組間差異,用迴歸模型的形式來描述yit=α0 α1Treat i α2Postt α3#Treati*Postt。這裡Treati=1代表個體是否受到干預,Postt##= 1代表幹預後觀測的時間週期。透過下表,我們可以發現α2 α#3##是實驗組在實驗日期前後的差分值,α2是對照組在實驗日期前後的差分值。對這兩項做差,α3即為因果效應的估計,也是上述模型中交互項的係數,並且就是兩次差分的結果。 雙差分法依賴比較嚴格的假設。 「平行趨勢」是最重要的前提,也就是實驗組和基準組再政策幹預發生前結果指標的均值隨著時間趨勢穩定,這預示著除了政策幹預本身其他因素影響對於實驗組和基準組是相同的。我們可以使用時間趨勢圖來檢驗平行假設,有些統計推斷套件也會提供對應的功能。當平行檢定不通過的時候,可以透過在迴歸中加入控制變數或時間趨勢項來進一步檢驗。在某些情況下,也可以藉助三重差分法來解決。此外在實際實務中,雙重差分法有比較多的實現方式。除了上文所述方式之外,也可以採取「雙向固定效應模型」的設定Yit=τTreatit Xitβ αi ξt εit,但也會依賴強假設:不存在隨時間變化的混淆因素,且過去的結果不會影響當期的處理狀態,同時也要求政策的處理效應保持不變。關於背後的理論和方法的局限性,以及拓展出的匹配和加權等新方法,推薦結合斯坦福大學徐軼事青教授的課程來進行學習: https://yiqingxu.org/teaching/ #下面我們列舉一些比較常用的新方法:# # 合成控制法是面板資料因果推論法中衍生出的一套方法,也在不斷的有新的估計值或統計推論檢定研究出現。當介入實施在一個群體或一個地區的時候,實驗組在一個時間點上只有一個觀測值,並且數據的時間週期較長,例如某個城市做地推活動,通常不適用於雙重差分的方法,這時候可以採取合成控制法。其原理是挑選一些對照城市,擬合成一個在幹預前和實驗組極其相似的“虛擬對照組”,詳細的理論介紹和近年來的優化可以參考麻省理工大學Aberto Abadie教授及其合作者的論文(Abadie, Diamond and Hainmueller 2010)和他在NBER的短期課程來進行進一步學習: https://www.nber.org/ lecture/2021-summer-institute-methods-lecture-alberto-abadie-synthetic-controls-methods-and-practice #雙差分法與合成控制法其實都可以統一在一套分析框架體系內。研究Arkhangelsky et al. (2021)指出,雙重差分是在解決一個沒有任何個體或時間上加權的雙向固定效應回歸問題,而合成控制法是在政策幹預發生前的個體施加權重ω來擬合被幹預的個體,這篇論文結合兩種方法提出了一個新的估計量:合成雙重差分(SDID),既包括個體上的權重ω,也包括時間上的權重λ,從而提升了整體估計量的穩健性效果。這裡的時間的權重λ可以理解為和乾預發生後更相似的時期的數據時期被賦予了更高的權重。 #幾種方法的比較:圖片來自論文 Arkhangelsky et al. ( 2021) 面板資料也可以結合矩陣補全的方法做因果推斷,這也是近年來這個領域的新發展。矩陣補全的演算法是透過解一個凸優化問題來解決因果推論面臨的反事實資料的缺失問題。這種方法適用於個體被政策幹預時間不一致的情況,例如一個產品的迭代需要用戶更新產品版本才生效,但是用戶更新的時間不一致。詳細的方法理論可以參考Athey et al. (2021)等相關論文。矩陣補全、合成控制還有隨機幹預下的迴歸預測方法也都可以統一在最佳化問題的框架下,進而我們也可以透過ensemble方式結合多種方法得到更穩健的估計結果(Athey et.al 2019) 。 矩陣補全示意圖:圖片來自Guidon Imbens在AEA的課程,此處用W代表treatment狀態https: //www.aeaweb.org/conference/cont-ed/2018-webcasts #以上在這一部分我們介紹了面板資料因果推斷的主要方法和進展,這個領域是一個方法非常多樣化、進展非常快的領域,但是對於應用者而言要求需要充分思考方法背後的假設和局限性,才能更加準確的評估實際中的各種政策,受篇幅限制這裡我們只是做了非常簡單的介紹。 結合機器學習方法來研究異質性因果效應其實是最近幾年因果推論發展的趨勢。我們先介紹異質性因果效應:異質性因果效應(Heterogeneous Treatment Effect,簡稱HTE)是指由於樣本個體特徵不同,實驗在個體上產生不同效果的現象。結合數學公式來表達,HTE有很多種形式: 每個個體的因果效應ITE (individual treatment effect):τi=Yi1-Yi0,Y i1和Yi0只有一個能觀測到,另一個和τi需要透過一定的模型方法來估計。 在某些特徵上的群體的平均因果效應,這裡我們用X代表特徵,那麼估計的是CATE (conditional average treatment effect)是限定特徵上去某些特定值的群體上的平均因果效應: τ(x)=E[Y1-Y0|X=x]。 HTE的分析方法目前有廣泛的應用情境。透過HTE,我們可以知道對某種策略幹預反應最大的群體有哪些特徵,也可以幫助我們排查一個A/B測試有預期效果或沒效果的策略的作用機制如何,還可以應用於各種個人化策略當中。異質性因果推斷的方法在工業界和互聯網有非常多的應用,例如在TripAdvisor用來計算在會員註冊激勵,在微軟用這類方法和短期數據測算不同項目的長期ROI,詳細的應用案例可以參考2021的KDD訓練課程(https://causal-machine-learning.github.io/kdd2021-tutorial/)。 最常見的異質性因果效應的方法其實是實驗分析中常用的多維分析,但多維分析的使用需要警惕多重檢定的問題。同時,當維度夠多時,對於實驗樣本量也有比較高的要求,同時分析效率比較低。而機器學習方法,則提供了一些提升效率的挖掘手段,它的好處是可以自適應地學習異質性因果效應的分佈,不需要嚴格的函數形式假設,比傳統基於線性回歸的計量經濟學方法或者多維分析的方法有更強的自由度,但對於技術上的挑戰是如何做統計推論。近年來隨著機器學習和計量經濟學的結合不斷深入,也有多套方法在這一領域有所創新和應用,這裡我們重點介紹以下幾類方法,這些方法成立的基本假設都是條件獨立假設( Conditional Independence Assumption),也就是說只有當各種混淆變數控制的足夠充分時,我們才能得到相對準確的因果效應估計。 因果森林:基於隨機森林,是直接進行擬合估計法的非參考方法。因果樹的主要估計邏輯是透過定義每片葉子上的因果效應,來定義整體樹的loss function。因果樹旨在根據某種切分X的方式,最大化所有葉片的loss的和。和機器學習中的樹算法除了估計的目標不同之外,還有一個差異點是在因果推斷的算法中一般會將訓練集樣本分成訓練集和估計集,訓練集用於分葉,估計集用於分葉後計算每個葉節點上的平均處理效應。因果樹的優點是結果非常簡潔易懂,可以透過分桶的方式直接明確實驗效果在哪些人群上有明確的差異,最先分桶的指標往往是最因果效果差異性的最大的維度。但因果樹容易過度擬合,在實際工作中推薦使用因果隨機森林(細節可參考Athey and Imbens 2016, Wager and Athey 2018),同時因果隨機森林也有比較好的統計推斷性質。關於此方法的拓展可以參考Athey, Tibshirani and Wager (2019)和Friedberg et al. (2020)等研究工作,這些新的方法可以進一步處理有混淆變數時的問題,以及更平滑地估計結果。 Meta Learners:和使用因果樹直接估計因果效應的模型不同,它屬於間接估計模型的一種:是透過對結果變數Y進行直接建模。因此Meta Learner無法將估計的HTE直接用於做統計推斷,在實際應用過程中,有些研究者會採用bootstrap方式來解決這個問題。 Meta Learners估計演算法有3種:T-Learner, S-Learner, X-Learner。三種方法基本的差異在於: 最簡單的是 S-learner。它將乾預變數作為了一個特徵變數進行一次建模,適合用在treatment和結果變數強相關的情況上,否則模型無法識別幹預變數改變引起的結果的改變; 稍微複雜一點的是T-learner。其透過強制用兩個模型分別學習實驗組的Yi1和控制組Yi0而辨識因果效應,適合用在實驗組和控制組變項觀測值較多且較平均的時候,否則其中一個模型會更被更重的regularized; #X-learner是一種較為新的方法,透過使用兩步估計和用傾向性得分糾偏,可以在資料量較少的情況下做出較好的估計(更多細節參考Künzel et al. 2019)。 基於DML和DRL的估計框架:這兩個框架我們結合微軟公司的Econml工具來介紹: https://www.microsoft.com/en-us/research/project/econml/ DML(double machine learning)雙重機器學習是針對高維混淆變數存在的情況下,靈活混淆變數和處理變數、結果變數之間關係的一種框架性的方法,其方法顧名思義,在估計因果效應的時候主要分為兩步:第一步用兩種(不需要同樣的)機器學習模型分別估計E(Y|X,W)和E(T|X,W)兩個條件期望,然後取殘差。這裡X和W都是混淆變量,但只有X是CATE中相關的變數。第二步是基於殘差進行ATE或CATE的估計,在估計CATE時,T-E(T|X,W)的殘差前乘以一個關於X的函數θ(X)來進行估計。關於如何估計ATE可以參考Chernozhukov et al. (2018)。 Econml在第二步驟提供了許多種模型來供選擇:LinearDML(用OLS模型)、DML(用自訂的模型)、CausalForestDML(用因果隨機森林)…。 DML框架在使用的時候需要注意檢驗兩個模型的殘差項是否均值顯著區別於0或顯著相關,如果是的話,說明混淆變數可能控制的不夠多。 DRL框架則是基於Doubly Robust方法,也是分成兩步,第一步使用X,W,T預測Y,定義預測值為gt(X,W);第二步驟用一個分類模型,用X,W預測T得到傾向分數,定義為p #t(X,W)。要注意的是這裡的T是離散變量,並且限制gt(X,W)某種regression-based model。兩步驟結果之後則是計算一個調整後的結果變數: 再將調整過後的Y i,tDR#在實驗組與控制組求差Y#i1DR#-Yi0DR,回歸X得到CATE。 DRL之所以叫Doubly Robust的原因在於,上述公式中gt#(X,W)和pt(X,W)中只要有一個估計正確,因果效果估計就是無偏的。但如果兩個模型估計都是錯誤的,那產生的誤差可能會非常大。同DML類似,Econml中DRL的各種Learner的差異在於使用什麼樣的模型來用X擬合Yi1##DR-Yi0DR 。 # 基於機器學習模型的異質性因果推論方法最大的應用挑戰其實是如何選擇合適的機器學習模型並且調參,得到相對穩健的估計結果。根據應用經驗和近年來的研究來說,有以下注意事項: 上述介紹的方法基本上還是集中在一個介入變數下的靜態的異質性因果效應。但是在實際應用中,我們會遇到的問題會更加複雜。例如涉及多個幹預變數:產品給使用者的補貼激勵中可能既包括簽到激勵,又包括一些其他任務的獎勵,怎麼平衡不同類型激勵的分配可以定義成一個多幹預變數的異質性因果效應建模和優化問題。再例如動態因果效應,混淆變數隨著不同時間的介入會進行變化(可參考Lewis and Syrgkanis 2020)。還是以激勵任務為例,這些任務可能讓使用者關注了新的主播、因而改變了她們的觀看內容的偏好,也會影響後續激勵的效果。這些複雜場景都激發了各類方法的進一步拓展,我們也期待未來會有更成型、更有體系化的研究和應用湧現。 在前一個部分我們介紹了潛在結果模型的主要想法和方法發展。這一類流派方法統計理論較為完善,可以得到比較準確的估計結果。但也存在一定的局限性,只能用來估計變數之間一度相關的影響(i.e,只允許有一個因變數和一些自變量,不能估計間接影響的連結),去如何學習眾多變數之間的連結和複雜關係,則需要用到另一個流派的結構因果模型方法。 結構因果模型以有向無環圖 (directed acyclic graph;DAG) 來描述變數間的因果關係和條件分佈。圖的每個節點是一個變量,因果關係由連結這些節點的邊來表示,例如X1 #2代表了X2#影響了X##1#,我們也稱X1為子節點,X2為父節點。對於一組隨機變數X=(X1,X2##,.. .,XP)形成的DAG,變數的聯合分佈可以表示成P(X)=∏pj=1P(Xj|pa##j),其中paj是Xj的緊鄰的父節點。當我們表達因果關係的時候,則引入do 算子的概念,假設當前X=(X#1,X 2,...Xp#)=(x##1#,x2,...xp),用do(Xj=x'j) 表示對於變數Xj介入(將其賦值為x'#j),那麼我們可以根據變數間的條件分佈關係得到一個新的DAG:P(X1=x1##,X2=x2,...,Xp=xp#|do(Xj=x'j)),新舊分佈下每個其他變數的期望變化就是X##j對他們的因果作用,例如E(X1#|do)(X##j=x'j)-E(X1##|do (Xj=x#j))。結果因果模型的開創者Judea Pearl在他的研究中指出,利用因果圖來識別因果關係的時候,如果滿足 “後門準則”和“前門準則”,其實並不需要觀測到所有的變量,關於具體的理論細節請參考Pearl (2009)。需要補充說明的是,結構因果模型和潛在結果模型其實也是存在關聯的。 在實際應用中,我們不一定能夠直接具備定義因果圖的信息,因此如何學習變數間的因果圖結構反而成為了重要的問題。在解決這類問題時,首先我們要明確所需的假設: #Causal Markov因果馬可夫假設:該假設意味任何節點的條件分佈僅基於其直接父節點。 Causal Sufficiency 因果充分性假設:此假設等同於不存在無法觀測的混淆變數。 Causal Faithfulness 因果忠誠性假設:此假設意義是基於一些條件機率分佈,一些節點之間是獨立的(因此圖可以被切割)。 其演算法大致分成兩類: #詳細介紹可以參考Glymour, Zhang and Sprites (2019)和《中國科學:數學》2018年12期的文章《因果推論的統計方法》: https://cosx. org/2022/10/causality-statistical-method/。 Constraint-based Algorithms:基於條件分佈獨立檢定學習出所有滿足faithfulness和causal markov假設的因果圖,即檢驗兩個節點之間的條件分佈是否獨立。例如PC演算法(Spirtes and Glymour 1991)和IC演算法(Verma and Pearl 1990)。 Score-based Algorithms:透過最最佳化定義的某種score來尋找和資料最匹配的圖結構。需要定義structural equations和score functions。例如CGNN演算法(Goudet et al. 2017)和NOTEARS演算法(Zheng et al. 2018)。這裡我們著重介紹一下NOTEARS演算法。傳統的演算法是基於在所有節點和節點間可能產生的關係的基礎上,在所有可能生成的圖中進行搜索,按照某個標準選出最優解決,這是典型的NP-hard的問題,耗時極長且目前的運算資源基本上無法滿足運算需求。 NOTEARS演算法將離散搜尋的問題轉化成了連續搜尋的問題。該演算法極大地提高了運算速度,使得普通的資料分析師也可以使用。但這個方法也存在著一定的局限性,例如假設所有變數的雜訊必須是高斯分佈,近年來也有越來越多的方法(如He et al.2021)嘗試改進這類方法的假設。 隨著強化學習領域的發展,我們也發現因果推論和強化學習可以相互結合在一起,推動相互的發展。因果推論可以在強化學習中透過推斷狀態之間或狀態與動作之間的因果關係,幫助強化學習演算法更有效率的學習價值函數或最優策略,在這方面有興趣的讀者可以參考哥倫比亞大學教授Elias Bareinboim的課程(https://www.php.cn/link/ad16fe8f92f051afbf656271afd7872d# )。在另一方面,強化學習也可以融入因果圖的學習演算法中,例如華為諾亞方舟實驗室的研究Zhu, Ng, and Chen (2019)。 關於因果推斷未來的展望,要提到近年來和圖學習、因果推斷、機器學習相關的一個新的研究範式,是清華大學崔鵬老師團隊提出的“穩定學習”的概念(Cui and Athey 2022)。機器學習、人工智慧等模型的應用依賴一個重要的假設——Independent and Identically Distributed(獨立同分佈)的假設。也就是說訓練集、測試集需要來自同一個分佈,但實際上存在各種各樣的OOD(Out Of Distribution,分佈外)問題,此時模型的表現無法保證,這也是歷史以來各類模型面臨的一個重要的技術風險。因果推斷可以幫助克服這類問題。如果可以確保一個結構在各種各樣的環境下都具有同等的預測效應從而克服OOD問題,那麼這個結構一定是一個因果結構,而且一個因果結構在各種環境下的表現都是相對穩定的。崔鵬老師團隊的研究(He et al. 2022, Shen et al. 2021)發現,利用混淆變數匹配平衡的思想,透過對樣本進行重加權就可以使得所有的變數變得獨立,使得一個基於關聯的模型變成基於因果的模型。所謂的穩定學習,就是使用一種分佈的訓練集和多種不同的未知分佈的測試集,優化的目標是最小化準確率的變異數。相信在未來這是一個非常重要的領域,有興趣的讀者可以繼續關注相關的研究進展。 獨立同分佈學習、遷移學習、穩定學習的比較:圖片來自論文Cui and Athey 2022 在實際應用中,推薦系統、電腦視覺、自動駕駛、自然語言處理等機器學習、人工智慧相關的領域都不乏因果推論和因果圖學習的身影,推動了這些領域的發展,在這裡我們也是列舉一些近年來的例子,關於更詳細地與機器學習相關的應用和benchmark模擬器、數據集可以參考UCL和牛津大學的研究者的總結(Kaddour et al. 2022)。在推薦系統領域,如我們在工具變數方法應用中的介紹,推薦系統不可避免地存在偏差,識別使用者和物品之間的因果圖關係可以幫助推薦系統糾偏。例如Wang et al. (2021)和Zhang et al. (2021)分別利用因果圖來消除標題黨和流行度帶來的偏差。在自動駕駛領域,來自微軟的研究者推出了一個模擬駕駛環境平台CausalCity(McDuff et al. 2022),將因果推論融入車輛的軌跡預測。在自然語言處理領域,研究者發現因果推論可以幫助NLP方法更加穩健和可理解(Zeng et al. 2020),包括檢驗語言模型和語料庫中的偏見(Vig et al. 2020)…相信在未來,因果推論會繼續蓬勃發展,在上述和其他領域中發揮重要的作用。 1、A/B測試
2、工具變數法
3、匹配法
4、面板資料的系列方法和發展

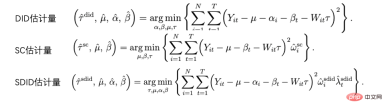

5、異質性因果效應的方法綜述
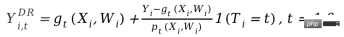
https://github.com/uber/causalml。
結構因果模型
以上是因果推論主要技術思想與方法總結的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 軟AI的興起及其對當今企業的意義Apr 15, 2025 am 11:36 AM
軟AI的興起及其對當今企業的意義Apr 15, 2025 am 11:36 AM軟AI(被定義為AI系統,旨在使用近似推理,模式識別和靈活的決策執行特定的狹窄任務 - 試圖通過擁抱歧義來模仿類似人類的思維。 但是這對業務意味著什麼
 為AI前沿的不斷發展的安全框架Apr 15, 2025 am 11:34 AM
為AI前沿的不斷發展的安全框架Apr 15, 2025 am 11:34 AM答案很明確 - 只是雲計算需要向雲本地安全工具轉變,AI需要專門為AI獨特需求而設計的新型安全解決方案。 雲計算和安全課程的興起 在
 生成AI的3種方法放大了企業家:當心平均值!Apr 15, 2025 am 11:33 AM
生成AI的3種方法放大了企業家:當心平均值!Apr 15, 2025 am 11:33 AM企業家,並使用AI和Generative AI來改善其業務。同時,重要的是要記住生成的AI,就像所有技術一樣,都是一個放大器 - 使得偉大和平庸,更糟。嚴格的2024研究O
 Andrew Ng的新簡短課程Apr 15, 2025 am 11:32 AM
Andrew Ng的新簡短課程Apr 15, 2025 am 11:32 AM解鎖嵌入模型的力量:深入研究安德魯·NG的新課程 想像一個未來,機器可以完全準確地理解和回答您的問題。 這不是科幻小說;多虧了AI的進步,它已成為R
 大語言模型(LLM)中的幻覺是不可避免的嗎?Apr 15, 2025 am 11:31 AM
大語言模型(LLM)中的幻覺是不可避免的嗎?Apr 15, 2025 am 11:31 AM大型語言模型(LLM)和不可避免的幻覺問題 您可能使用了諸如Chatgpt,Claude和Gemini之類的AI模型。 這些都是大型語言模型(LLM)的示例,在大規模文本數據集上訓練的功能強大的AI系統
 60%的問題 - AI搜索如何消耗您的流量Apr 15, 2025 am 11:28 AM
60%的問題 - AI搜索如何消耗您的流量Apr 15, 2025 am 11:28 AM最近的研究表明,根據行業和搜索類型,AI概述可能導致有機交通下降15-64%。這種根本性的變化導致營銷人員重新考慮其在數字可見性方面的整個策略。 新的
 麻省理工學院媒體實驗室將人類蓬勃發展成為AI R&D的核心Apr 15, 2025 am 11:26 AM
麻省理工學院媒體實驗室將人類蓬勃發展成為AI R&D的核心Apr 15, 2025 am 11:26 AM埃隆大學(Elon University)想像的數字未來中心的最新報告對近300名全球技術專家進行了調查。由此產生的報告“ 2035年成為人類”,得出的結論是,大多數人擔心AI系統加深的採用


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

SAP NetWeaver Server Adapter for Eclipse
將Eclipse與SAP NetWeaver應用伺服器整合。

mPDF
mPDF是一個PHP庫,可以從UTF-8編碼的HTML產生PDF檔案。原作者Ian Back編寫mPDF以從他的網站上「即時」輸出PDF文件,並處理不同的語言。與原始腳本如HTML2FPDF相比,它的速度較慢,並且在使用Unicode字體時產生的檔案較大,但支援CSS樣式等,並進行了大量增強。支援幾乎所有語言,包括RTL(阿拉伯語和希伯來語)和CJK(中日韓)。支援嵌套的區塊級元素(如P、DIV),

Dreamweaver Mac版
視覺化網頁開發工具

ZendStudio 13.5.1 Mac
強大的PHP整合開發環境

MinGW - Minimalist GNU for Windows
這個專案正在遷移到osdn.net/projects/mingw的過程中,你可以繼續在那裡關注我們。 MinGW:GNU編譯器集合(GCC)的本機Windows移植版本,可自由分發的導入函式庫和用於建置本機Windows應用程式的頭檔;包括對MSVC執行時間的擴展,以支援C99功能。 MinGW的所有軟體都可以在64位元Windows平台上運作。







