圖神經網路發Nature子刊，卻被爆比一般演算法慢104倍，質疑者：灌水新高度？

GNN 是近年來非常火熱的一個領域。最近，一篇 Nature 子刊論文提出了一種用 GNN 解決組合來優化問題的方法，並聲稱該 GNN 優化器的性能與現有的求解器相當，甚至超過了現有的求解器。不過，這篇論文引來了一些質疑：有人指出，這個GNN 的效能其實還不如經典的貪心演算法，而且速度還比貪心演算法慢很多（對於有一百萬個變數的問題，貪心演算法比GNN快104 倍）。所以質疑者表示，「我們看不出有什麼好的理由用這些GNN 來解決這個問題，就像用大錘砸堅果一樣。」他們希望這些論文作者能夠在宣稱方法優越性之前，先和困難問題的基準比較一下。

近年來，神經網路解決了應用程式和基礎科學方面的許多難題，其中就包括離散組合最佳化問題，這也是我們理解計算極限的基礎。

Martin JA Schuetz 等人2022 年的研究《Combinatorial optimization with physics-inspired graph neural networks》[4]提出使用受物理啟發的無監督圖神經網路（GNN）來解決圖上的組合最佳化問題，這種方法似乎很有前途，並發表在具有高影響力的期刊（《自然· 機器智能》）上。該研究測試了 GNN 在兩個標準最佳化問題上的性能：最大切割和最大獨立集（MIS）。這種新提出的 GNN 優化器有一個非常好的功能：它可以擴展到許多更大的實例問題。

論文網址：https://arxiv.org/pdf/2107.01188.pdf

#不過，最近一篇新論文《Cracking nuts with a sledgehammer: when modern graph neural networks do worse than classical greedy algorithms》對Martin JA Schuetz 等人的研究提出了質疑，認為Martin JA Schuetz 等人提出的GNN 優化器是「用大錘敲堅果（ Cracking nuts with a sledgehammer ），類似於迫擊砲打蚊子”，既浪費資源，效果也不好。

論文網址：https://arxiv.org/abs/2206.13211

#MIS 問題的定義如下：給定一個具有n 個節點、度固定為d 的無向隨機正則圖（d-RRG），獨立集（IS）是指不包含任何最近鄰對的頂點子集；MIS 問題需要找出最大的IS，其大小稱為α。 MIS 是一個 NP-hard 問題，但人們希望找到一種演算法，以在多項式時間內找到一個大小盡可能接近最大值的 IS。此外，一個好演算法不應因為 n 值較大而效能降低。

Martin JA Schuetz 等人提出的新型GNN 可以為非常大的圖（n≤ 10^6）找到IS：演算法運行時間與問題大小成比例：t∼ n^ 1.7，且演算法效能隨著n 的增加保持穩定，如下圖1 所示。

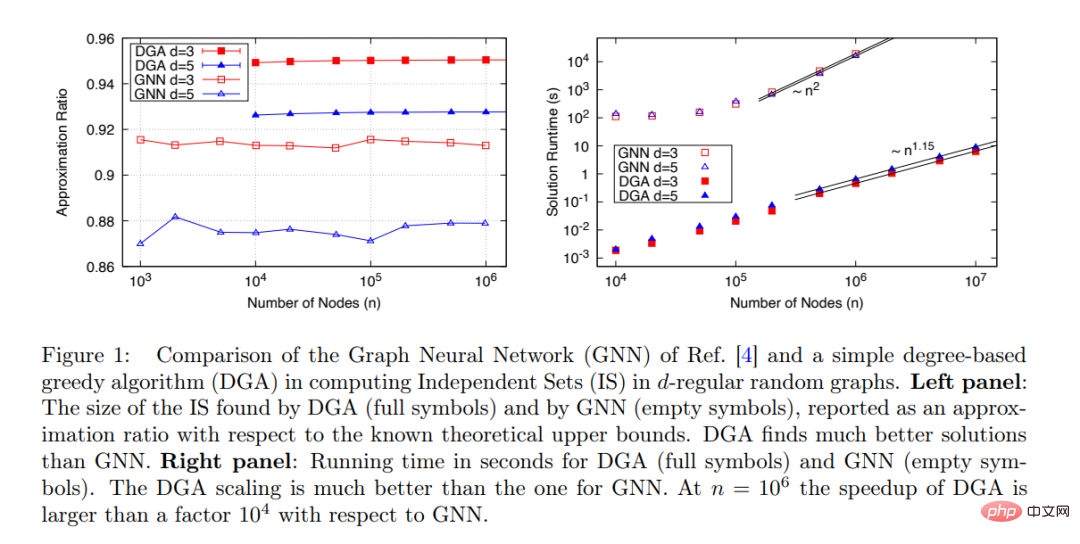
然而，當所提GNN 與其他可用演算法進行效能比較時，研究僅與Boppana- Halldorsson（BH）近似演算法[8] 做了比較，該演算法在n≤ 500 時，運行時間t∼n^2.9。

實際上還有許多其他計算 IS 的演算法比 BH 快得多，該研究應該將所提 GNN 最佳化器與這些演算法進行比較。其中，最簡單的演算法就是貪心演算法（GA）[9]。基於度數的貪心演算法（DGA）經過最佳化後，運行時間幾乎與節點數目 n 呈線性關係。

研究比較了Martin JA Schuetz 等人提出的GNN 優化器（空心）和DGA（實心）在d=3 和d=5 的d-RRG 上找到MIS的性能。 如圖1（右）所示，從運行時間與問題大小（節點數）的關係來看，DGA 比GNN 好得多，前者的運行時間幾乎與節點數n 呈線性關係（指數是1.15 可能是由於預漸近效應），而GNN 的運行時間與節點數n 幾乎呈二次關係。

#

該研究認為Martin JA Schuetz 等人的主張「基於圖神經網路的優化器的性能與現有的求解器相當或優於現有的求解器，具有超越當前SOTA 模型的能力，能夠擴展到具有數百萬個變數的問題」，經不起推敲，與實際實驗結果不一致，Martin JA Schuetz 等人應對論文予以修改。

該研究詳細闡明了DGA 的性能，並認為這種簡單的貪心演算法應該被視為一個最低基準，任何新演算法的性能必須至少比DGA好才能被採用。

當然，DGA 只是一種極為簡單的演算法，還有許多其他標準演算法優於 DGA。 Maria Chiara 等人 2019 年的論文《Monte carlo algorithms are very effective in finding the largest independent set in sparse random graphs》對多個解決 MIS 問題的演算法性能進行了深入的研究。

基於此，研究提出一個問題：「評估一個新的最佳化演算法時，應該用什麼真正困難的問題作為測試演算法效能的基準？」

例如，研究認為，在d16 的d-RRG 上的MIS。這裡可以將 d=20 和 d=100 的結果與 2019 年論文《Monte carlo algorithms are very effective in finding the largest independent set in sparse random graphs》中給出的結果進行比較。

顯然，一個好的最佳化演算法應該在n 的多項式時間內完成，如果呈線性關係就更好了，找到的解的品質應優於簡單的現有演算法，並且不應隨著n 的增加而質量有所下滑。

該研究總結：目前，基於神經網路的優化器（如Martin JA Schuetz 等人提出的優化器）不滿足上述要求，並且無法與簡單的標準演算法競爭以解決困難的最佳化問題。探究神經網路是否可以滿足這項要求，或者它們的失敗是否有更深層的原因，這一點至關重要。

以上是圖神經網路發Nature子刊，卻被爆比一般演算法慢104倍，質疑者：灌水新高度？的詳細內容。更多資訊請關注PHP中文網其他相關文章！