動畫製作效率提升80%！這個AI軟體一鍵實現高精度視訊動捕

AIGC 又出新魔法了！

不用動畫師手 K、慣捕或光捕，只需提供一段視頻，這個 AI 動捕軟體就能自動輸出動作。只要短短幾分鐘，虛擬人的動畫製作就搞定了。

不僅是四肢大框架動作，連手部的細節都能精準捕捉。

除了單視角視頻，還能支援多個視角的視頻，相較於其他只支援單目辨識的動捕軟體，該軟體能提供更高的動捕品質。

同時，軟體也支援對辨識的人體關鍵點、平滑度、腳步細節等進行編輯修改。從一般玩家的興趣體驗，到硬派玩家的專業需求，它都可滿足。

這就是網易互娛AI Lab 深根多年、結合專業美術回饋不斷迭代優化、低調開發的AIxPose視訊動捕軟體。據悉，該軟體已經處理了超過數十個小時的影片資源，並應用於遊戲劇情動畫、熱門舞蹈動畫等資源的製作流程。經實際項目驗證，1 分鐘的舞蹈動畫，美術手工製作或需 20 多天，用 AIxPose 輔助製作僅需 3 天，整個流程縮短了 80% 以上。

近日，網易互娛AI Lab 基於開發該軟體的經驗，並結合在動捕領域的相關研究工作進行了整理，其所撰寫的論文《Learning Analytical Posterior Probability for Human Mesh Recovery》被電腦視覺頂會CVPR 2023 接收。

• 主頁網址：https://netease-gameai.github.io/ProPose/
• #論文網址：https://netease-gameai.github.io/ProPose/static/assets/CVPR2023_ProPose.pdf

##這篇論文創新地提出了一種基於後驗機率的視訊動捕技術ProPose，能夠在單張影像、多感測器融合等不同設定下實現準確的三維人體姿態估計。技術精度比使用先驗的基準機率方法高了 19%，且在公開資料集 3DPW、Human3.6M 和 AGORA 上均超越了過去的方法。此外，對於多感測器融合任務，該技術也能達到比基準模型更高的精度，且無需因為引入新感測器而修改神經網路的骨幹部分。

技術背景

本研究的任務是從RGB 影像中預測人體姿態和外形（human mesh recovery, hmr），現有的方法可以歸納為兩類：直接法和間接法。直接法採用神經網路端對端地回歸人體關節的旋轉表示（如軸角、旋轉矩陣、6D 向量等），而間接法先預測一些中間表示（如三維關鍵點、分割等），然後通過這些中間表示得到關節旋轉。

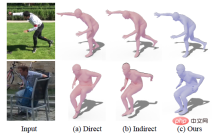
然而，這兩類方法都存在著一些問題。對於直接法而言，由於這類方法需要網路直接學習旋轉這類抽象表示，與學習關鍵點、分割相比，學習旋轉相對困難，因此網路輸出的結果有時很難和圖像對齊，且無法完成一些大幅度的動作，如下圖(a) 第一行的右腳無法完全向後伸展。與之相比，間接法一般能產生更高的精度，但是這類方法的表現很大程度上依賴於中間表示的準確性，當中間表示由於噪聲產生誤差時，容易讓最終的旋轉出現相當明顯的錯誤，如下圖(b) 第二行的左手所示。

除了前述這些確定性的方法，還有一些方法透過學習某些機率分佈來建模人體姿態的不確定性，從而將噪音納入考慮，提高系統穩健性。目前主要的機率建模方式包括多元高斯分佈、標準化流、神經網路隱式建模等，但這些非 SO (3) 上的機率分佈無法真實反映關節旋轉的不確定性。例如在不確定性較大時，高斯分佈在 SO (3) 上的局部線性假設不成立。近期的工作直接用網路學習了matrix Fisher 分佈的參數，雖然這是一種SO (3) 上的分佈，但該方法的學習方式和直接法類似，收斂表現無法和現有的間接法相比。

為了同時兼顧高準確性和穩健性，提升機率方法的性能，ProPose 推導了關節旋轉的解析後驗機率，不僅能夠受益於不同觀測變數帶來的高精度，也能衡量不確定性，盡可能減弱雜訊對演算法的影響。如下圖所示，對​​於輸入的圖片，ProPose 可以透過輸出的機率分佈一定程度上度量該關節旋轉在各個方向的不確定性，如右手沿著手臂軸的旋轉、左手臂上下擺動的朝向、左小腿遠近的程度等。

技術實作

人體建模

本研究對人體姿態進行機率建構模，目標是求關節旋轉R 在一些觀測變數條件下（如骨骼朝向d 等）的後驗機率p (R|d,⋯)。

具體而言，由於人體的關節旋轉位於SO (3) 上，而子關節相對於父關節的單位骨骼朝向位於S^2 上，因此可基於這兩種流形上的機率分佈進行分析。

首先，SO (3) 上的matrix Fisher 分佈MF (⋅) 可作為關節旋轉R 的先驗分佈，如下式所示，F∈R^(3×3 ) 是此分佈的參數，c (F) 是歸一化常數，tr 表示矩陣的跡。

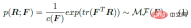
如下式所示，F 可以透過SVD 分解直接求解均值M 和一個表徵分佈聚集程度的聚集項K。其中，Δ=diag (1,1,|UV|) 為對角正交矩陣，用來確保 M 的行列式為 1，因而能落在特殊正交群中。

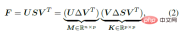
其次，考慮到骨骼的朝向能透過關節旋轉計算得到，因此可將關節旋轉R 看作隱變量，骨骼朝向d 作為觀測變量，給定R 的條件下，S^2 上的單位朝向d 服從von Mises-Fisher 分佈：

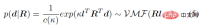
其中，κ∈R 和d∈S^2 分別是該分佈的聚集項和平均值，l 是參考姿態下（如T-pose）的單位骨骼朝向，理論上滿足Rl= d，即透過關節旋轉將參考骨骼朝向轉到目前骨骼朝向。

利用貝葉斯理論，給定先驗分佈p (R) 和似然函數p (d|R)，可以計算以骨骼朝向為條件的關節旋轉的後驗機率p (R|d) 的解析形式：

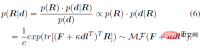
#由此可得到結論：後驗機率p ( R|d) 同樣服從matrix Fisher 分佈，且其參數從F 更新為F^'=F κdl^T。

上述後驗機率只考慮了人體骨骼朝向作為觀測量，類似地，還可以推廣到其它的方向觀測量d_i 或旋轉觀測量D_j（可由別的感測器產生，如IMUs 等），得到如下一般形式的解析後驗機率：

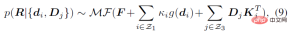
其中 κ_i 和 K_j 是聚集項。 g (⋅) 是一個 IK 形式的映射，能夠將方向觀測量轉換到旋轉估計，可以採用最簡單的形式如 g (d_i )=dl^T。 Z_1 和 Z_3 分別表示方向觀測量和旋轉觀測量的集合。

特性

這部分進一步闡述後驗機率分佈相較於先驗機率分佈有更高的聚集程度。

前述部分介紹了人體關節旋轉後驗機率的解析形式，該機率由一個新的參數 F' 來表徵。可以從另一個角度來理解後驗參數F^'，即F^' 是與F 相同的均值項M 和一個新的聚集項K^' 的乘積：

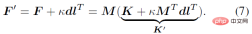
其中M^T dl^T=ll^T 是秩1 實對稱矩陣，而K 也是一個實對稱矩陣，即後驗的聚集項K' 同樣是實對稱矩陣。根據矩陣分析中關於實對稱矩陣的交錯定理，可以得到K' 的特徵值λ_i' 和K 的特徵值λ_i 有以下不等式關係：

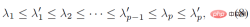
考慮到聚集項的特徵值等價於分佈參數的奇異值，而分佈參數的奇異值能反映該分佈的置信度，因此可以得到結論，當似然項非零時，後驗估計比先驗估計更集中，可以快速收斂到似然函數偏好的那個mode 上，以便更容易被學習。

除了先驗機率方法，另一類主要的基準方法是利用逆運動學（IK）直接透過骨骼朝向計算旋轉，下面這張圖可以直觀地展示後驗機率方法和確定性IK 方法之間的對比。

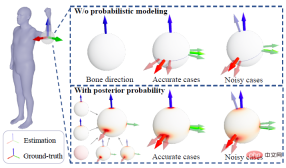
上圖以人體手肘關節為例。實的三維座標軸表示真實值，透明三維座標軸表示估計值。第一行表示確定性IK 方法，這類方法背後的建模方式是一個表示骨骼朝向的向量，當骨骼朝向估計準確時，剩餘的一個自由度（twist）便能縮小到一個圓上（圖中球上的虛擬線圈）；當骨骼朝向估計不準確時，則會使得所有可能的估計值都與真實值偏離。第二行表示本研究的後驗機率模型，由多個不同類型的模型融合而成，球面上的紅色區域表示某個旋轉的機率，即便骨骼朝向估計有誤差，這種方式也有可能恢復到真實值，因為骨骼朝向的雜訊能夠被先驗或其它觀測量所盡可能緩解。

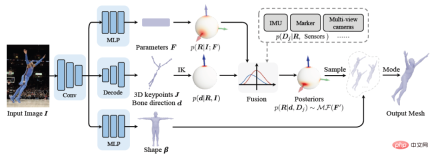
網路框架圖與損失函數

#基於前述理論與推導，可以直接建構出下圖所示的框架圖。利用多分支網路從單張圖片估計先驗分佈參數 F、三維關鍵點 J（從中計算出骨骼朝向 d）、外形參數 β。透過貝葉斯法則計算得到後驗機率，最終可從後驗分佈中得到姿態估計，從而輸出人體 mesh。

損失函數的選擇比較直接，如下四個約束的加權和，其中L_J 表示關鍵點約束，L_β 表示外形參數約束， L_θ 表示矩陣形式的姿態參數約束，L_s 表示對分佈進行取樣後的姿態約束。關於分佈的約束，這裡並未直接採用 MAP 是考慮了歸一化參數的數值穩定性問題。關於採樣策略，類似先前的工作，將 matrix Fisher 分佈轉為等價的四元數形式的 Bingham 分佈，然後透過拒絕採樣得到，其中拒絕採樣的建議分佈採用 angular central Gaussian 分佈。

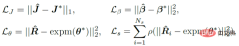
實驗結果

實驗部分，本研究在公開資料集 Human3.6M、3DPW、AGORA、TotalCapture 上和過去方法進行了定量對比。可以看到，本研究的方法超越了過去的一眾方法。其中右下表中最後灰色的兩行是同期工作，這裡為了榜單完整性也列了出來。

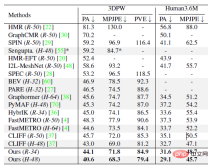
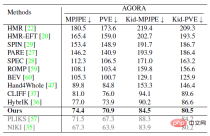
#下圖展示了和現有SOTA方法HybrIK、PARE、CLIFF 的定性對比，可以看到一些遮蔽的情況，ProPose 可以得到更好的效果。

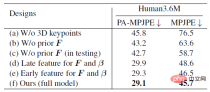
下表展示了一系列消融實驗，主要展示 ProPose 的準確度和穩健性。基準方法包括不使用三維關鍵點、不使用先驗、測試時不使用先驗、骨幹網路不同位置特徵的選擇等，下面左表充分驗證了所提出的後驗機率分佈有著更高的精確度。下面右表則展示了後驗方法和確定性 IK 方法對雜訊的穩健性比較，可以看到後驗方法能夠更大程度地抵禦雜訊的干擾。

#除了上述hmr 任務，本研究還在多感測器融合的任務上進行了評估，下面給出了一個單視角和IMUs 融合的效果。

以上是動畫製作效率提升80%！這個AI軟體一鍵實現高精度視訊動捕的詳細內容。更多資訊請關注PHP中文網其他相關文章！