時序分析五邊形戰士！清華提出TimesNet：預測、填補、分類、偵測全面領先

實現任務通用是深度學習基礎模型研究的核心問題，也是近期大模型方向的主要關注點之一。

然而，在時間序列領域，各類別分析任務的差異較大，既有需要細粒度建模的預測任務，也有需要擷取高層語意資訊的分類任務。 如何建構統一的深度基礎模型有效率地完成各類時序分析任務，此前尚未有成型方案。

為此，來自清華大學軟體學院的團隊圍繞時序變化建模這一基本問題展開研究，提出了任務通用的時序基礎模型TimesNet，論文被ICLR 2023接收。

作者表：吳海旭*，胡騰戈*，劉雍*，週航，王建民，龍明盛

連結：https://openreview.net/pdf?id=ju_Uqw384Oq

程式碼：https://github.com/thuml/TimesNet

時序演算法庫：https://github.com/thuml/Time-Series-Library

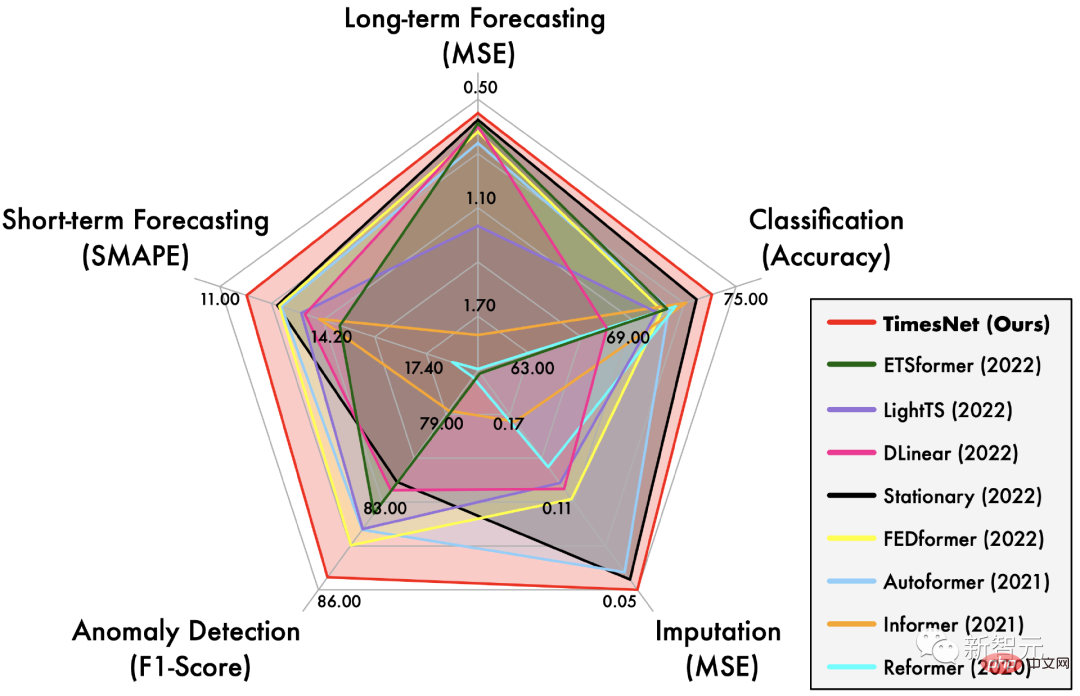
TimesNet在長時、短時預測、缺失值填補、異常檢測、分類五大任務上實現了全面領先。

1 問題分析

#不同於自然語言、影片等序列數據，時間序列中單個時刻僅保存了一些標量，其關鍵訊息更多地被蘊含在時序變化（Temporal Variation）中。

因此，建模時序變化是各類別時序分析任務共同的核心問題。

近年來，各類深度模型被廣泛用於時序分析任務中，例如循環神經網路（RNN）、時序卷積網路（TCN）和變換器網絡（Transformer）。

然而，前兩類方法主要關注捕捉臨近時刻之間的變化，在長期依賴上建模能力不足。

Transformer雖然在建模長期依賴上具有天然優勢，但是由於現實世界的時序變化極其複雜，僅僅依靠離散時間點之間的注意力（Attention）難以挖掘出可靠的時序依賴。

為此，本文從一個全新的多周期（Multi-periodicity）視角對時序變化進行了分析，如下圖所示。我們觀察到：

• 時間序列自然有#多週期性。

現實世界的時序資料往往是不同週期過程的相互疊加，例如交通資料在短期內的以日為週期變化，而長期則以星期為週期變化。這些不同周期的資料互相疊加、互相干擾，為時間序列分析帶來了極大挑戰。

• 時間序列呈現週期內與週期間兩種時序變化。

具體地，對於某一特定週期的過程，每個時間點的變化既與臨近時刻有關，也與臨近週期的相似過程高度相關。其中週期內變化對應著短期過程，週期間變化則可以反應連續週期間的長期趨勢。註：如果時間序列沒有明顯週期性，則等價於週期無限長的情況。

2 設計想法

基於上述兩點觀察，我們對TimesNet的結構進行如下設計：

• 時間序列的多週期性#自然地啟發了一個模組化（Modular）的設計思路，​​即一個模組捕捉由某一特定週期主導的時序變化。這種模組化的設計思路可以將複雜的時間變化解耦，有利於後續建模。
• 對於時間序列的#週期內與週期間變化，本文創新地提出

##將一維時序資料擴展至二維空間

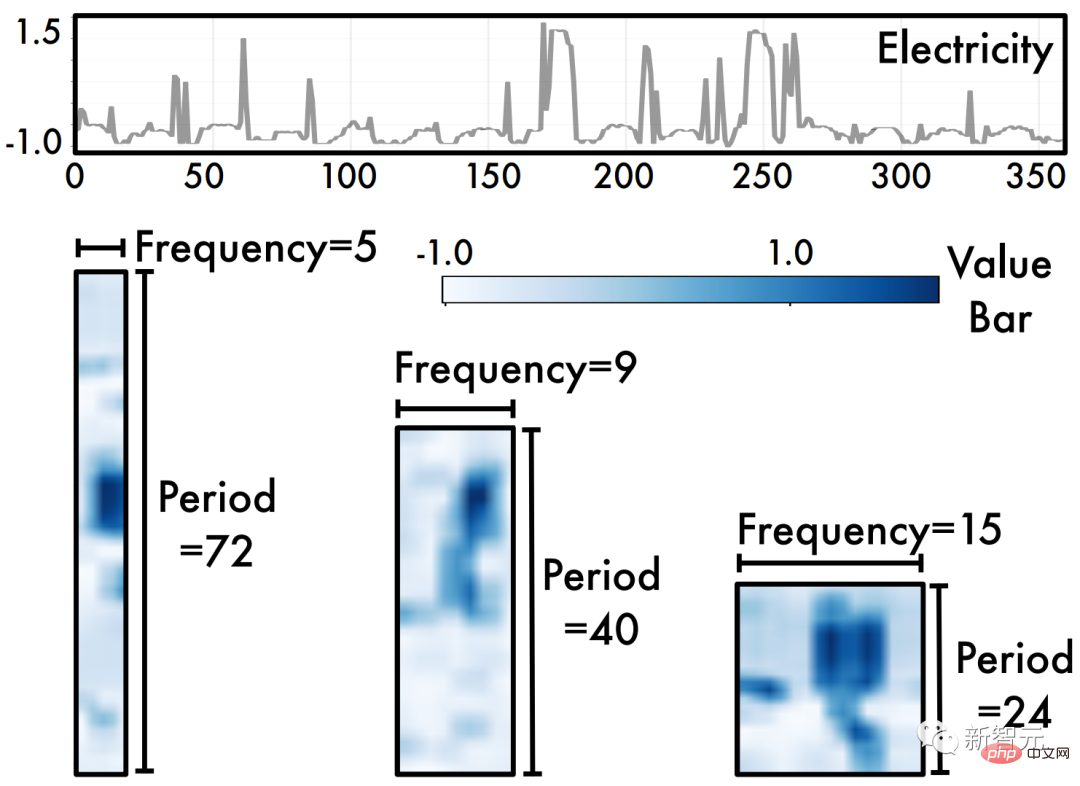
進行分析。如上圖所示，將一維時間序列基於多個週期進行折疊，可以得到多個二維張量（2D tensors），每個二維張量的列和行分別反應了周期內與週期間的時序變化，即得到了

二維時序變化（Temporal 2D-variations）。

上圖範例展示了將一維時序資料折疊至二維空間的視覺化效果。此處，Period方向反應週期內變化，而Frequency方向代表週期間變化。我們可以看出轉換至二維空間的時序資料具有明顯的二維局部性（2D locality）。

因此，在折疊時序資料後，我們可以直接採用先進的視覺骨幹網路

對時序資料進行特徵提取，例如Swin Transformer、ResNeXt、ConvNeXt等。

這種設計也使得時序分析任務可以直接受益於蓬勃發展的電腦視覺領域。

3 TimesNet

基於上述思路，我們提出了TimesNet模型，透過模組化結構將複雜時序變化分解至不同週期，並透過將原始一維時間序列轉換至二維空間

實現了週期內與週期間變化的統一建模。 在這一節中，我們將先介紹將時序資料擴展至二維空間的方法，然後再介紹模型的整體架構。

3.1 時序變更：1D->2D

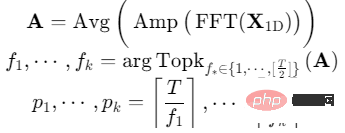#時序摺疊的流程如上圖所示，主要分為以下兩步驟：

（1）週期擷取#對於一個時間長度為、通道維度為的一維時間序列，可以由時間維度的快速傅立葉變換（FFT）直接提取週期信息，即：

其中，代表了中每個頻率分量的強度，強度最大的個頻率對應著最顯著的週期長度。

（2）序列折疊1D->2D

對於選定的個週期，分別對原始的一維時間序列進行折疊，該過程可以形式化為： 

#其中，為在序列末尾補0，使得序列長度可以被整除。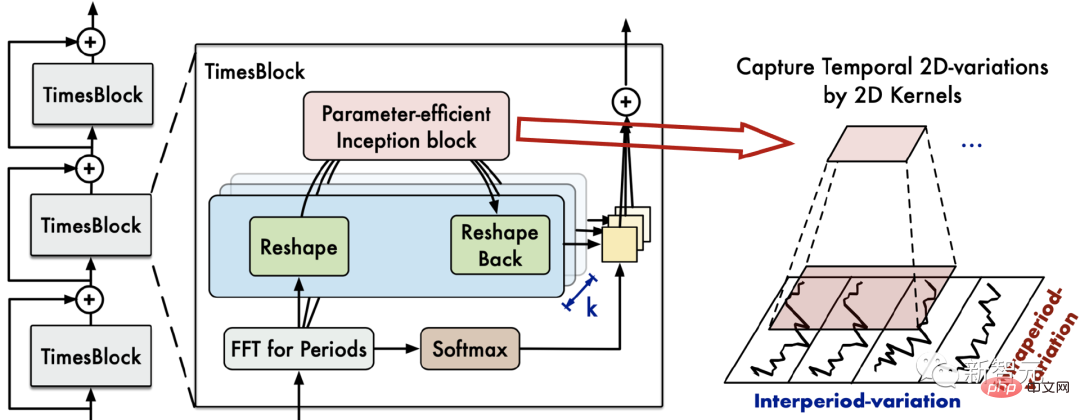

透過上述操作，我們得到了一組二維張量，其中對應週期為的二維時序變化。

###3.2 模型設計############TimesNet的整體架構如圖所示：############# #############整體上，TimesNet由堆疊的TimesBlock組成。輸入序列首先經過嵌入層得到深度特徵。對於第層TimesBlock，其輸入為，輸出為：######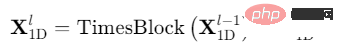

具體地，如下圖所示，每個TimesBlock包含下列子程序：

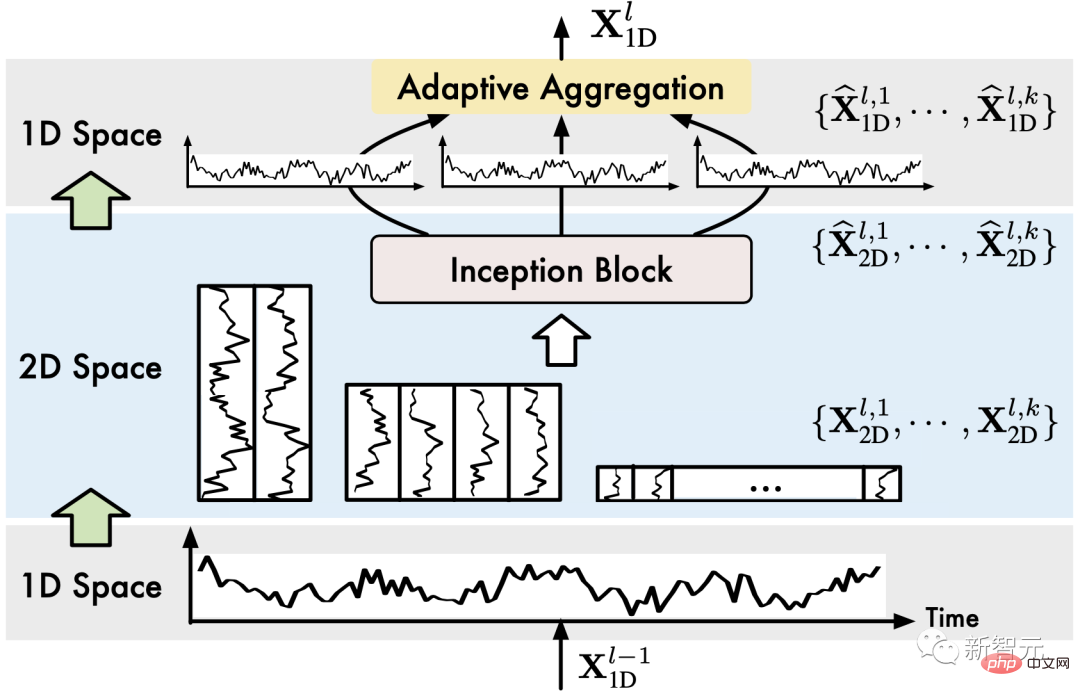
##（1）折疊時間序列（1D->2D）：TimesBlock首先對輸入的一維時序特徵提取週期，然後將其轉換成為二維時序變化，即上一節所涉及的內容：

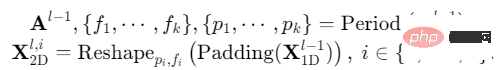
#（2）擷取二維時序變化表徵（2D Representation）：如前分析，轉換得到的二維時序變化具有2D局部性，因此可以直接使用2D卷積來提取特徵。此處，我們選用了經典的Inception模型，即：

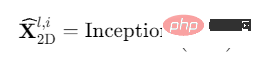
#值得注意的是，因為我們已經將1D時序特徵轉換至2D空間，所以我們也可以利用許多電腦視覺領域的前沿模型，例如ResNeXt、ConvNeXt以及基於Attention的Swin Transformer等等。這使得時間序列分析可以與視覺骨幹網路協同並進。

（3）展開時間序列（2D->1D）：為了後續多週期融合，我們將二維時序變化表徵展開至一維度空間：

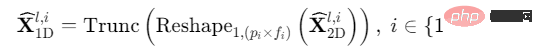
Trunc(⋅)表示將步驟（1）中Padding(⋅)操作補充的0去除。

（4）自適應融合（1D Aggregation）：為融合多週期訊息，我們將擷取到的二維時序表徵進行加權求和，選用的求和權重即為步驟（1）中得到的對應頻率強度：

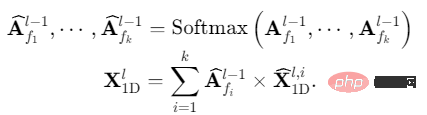
透過將1D時間序列轉換至2D空間的設計，TimesNet實現了「多個週期分別提取二維時序變化，再進行自適應融合」的時序變化建模過程。

4 實驗

我們在長時預測、短時預測、缺失值填補、異常檢測、分類五大任務上進行了實驗，涵蓋36個資料集、81種不同的實驗設定。

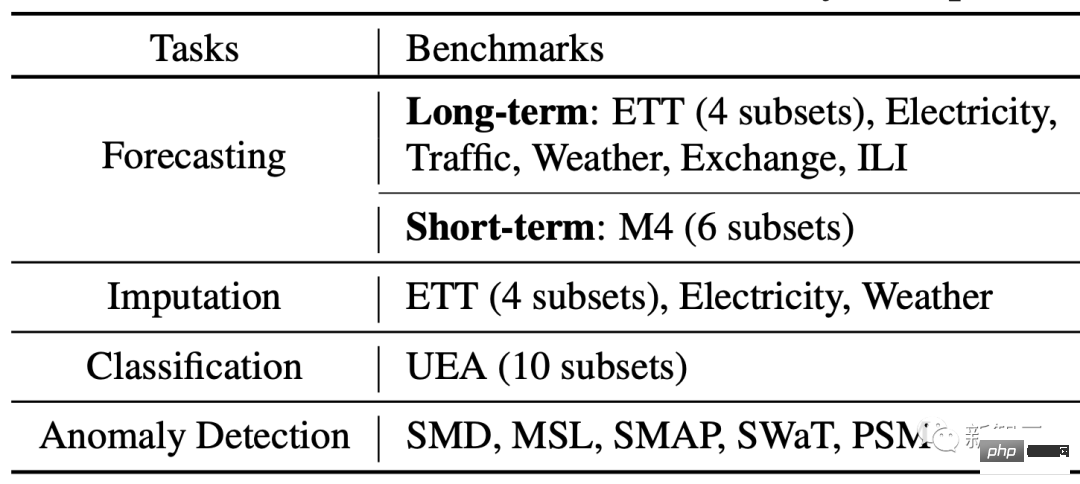
同時，比較了19種不同的深度方法，包含最新的基於RNN、CNN、MLP、Transformer的模型，例如N-BEATS（2019），Autoformer（2021），LSSL（2022），N-Hits（2022），FEDformer（2022），Dlinear（2023）等。

4.1 整體結果

如開篇雷達圖所示，TimesNet在五項任務上都達到了SOTA。

（1）長時預測：在此備受關注的任務上，TimesNet超過了先進的基於Transformer與MLP的模型。

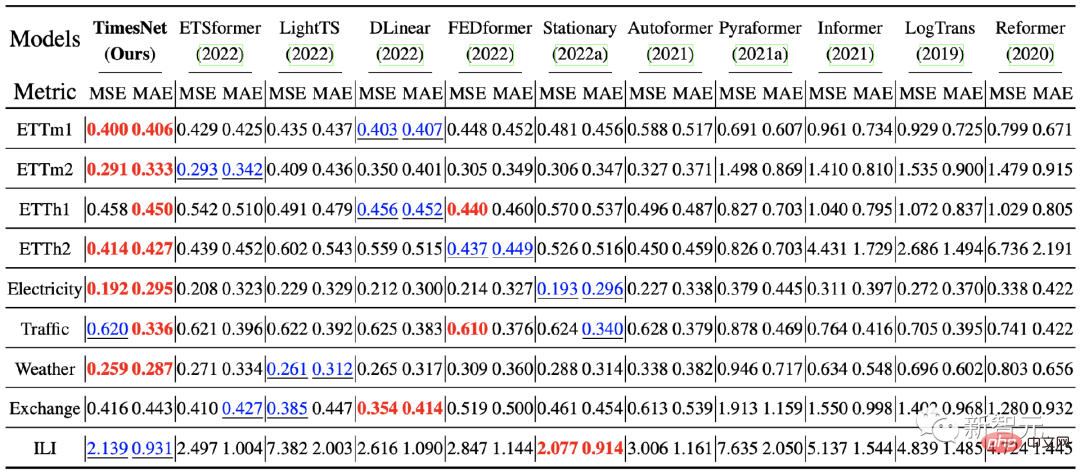
（2）短時間預測：此實驗中使用的M4資料集包含6個不同取樣頻率的子資料集，總共超過10萬個資料。 TimesNet在此複雜資料分佈情況下依然取得了最優的效果，驗證了模型的時序變化建模能力。

（3）分類任務：在此任務上，TimesNet超過了經典的Rocket演算法以及前緣深度學習模型Flowformer。

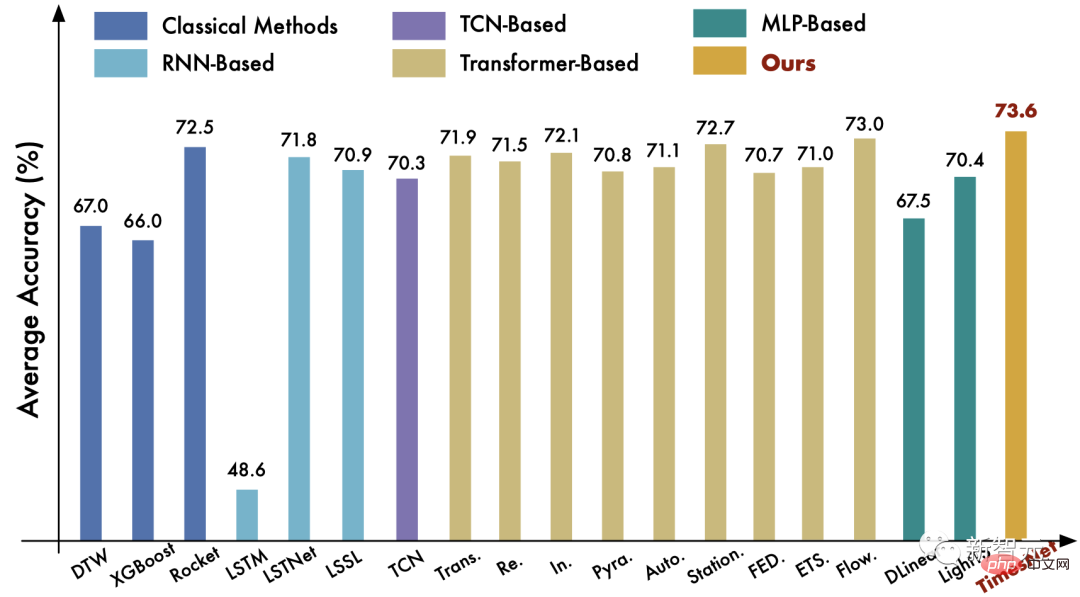
更多任務的比較請見論文。

4.2 視覺骨幹網路的泛化性

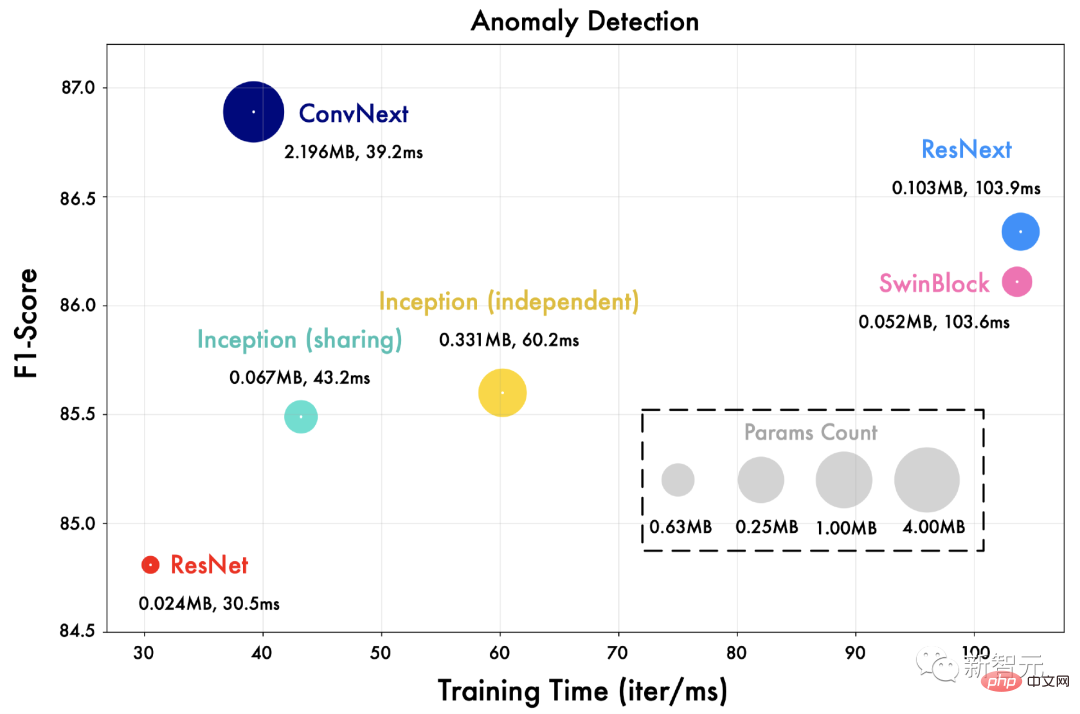
我們將TimesNet中的Inception網路替換為不同的視覺骨幹網絡，例如ResNet，ConvNext，Swin Transformer等。

如下圖所示，更先進的視覺骨幹網路可以帶來更優秀的效果。這也意味著在TimesNet的框架下，時間序列分析可以直接受益於視覺骨幹網路領域的進展。

4.3 表徵分析

為了進一步探討TimesNet的效果來源，我們展示了「模型底層-頂層表徵之間的CKA相似度」與「模型效果」之間的關係。其中，CKA相似度越低，代表模型底層-頂層之間的表徵差異越大，也就是更層次化的表徵。

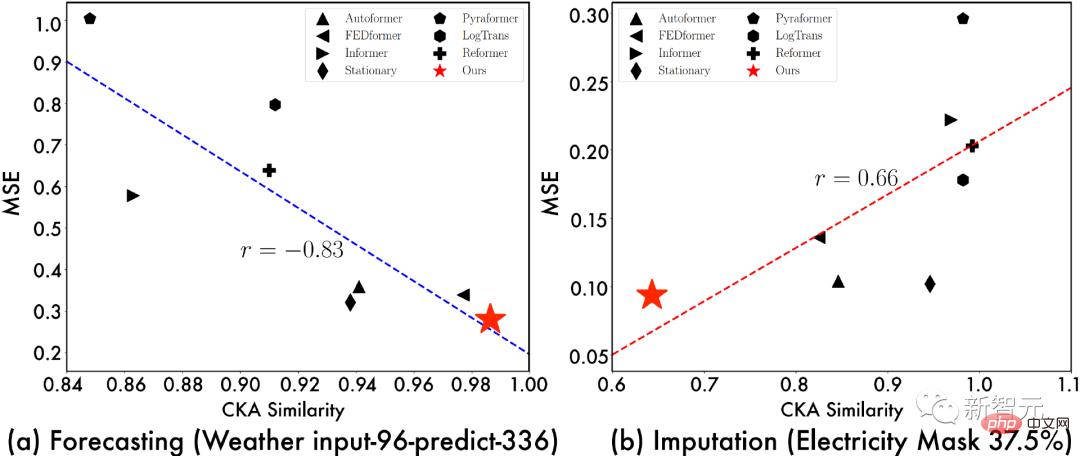
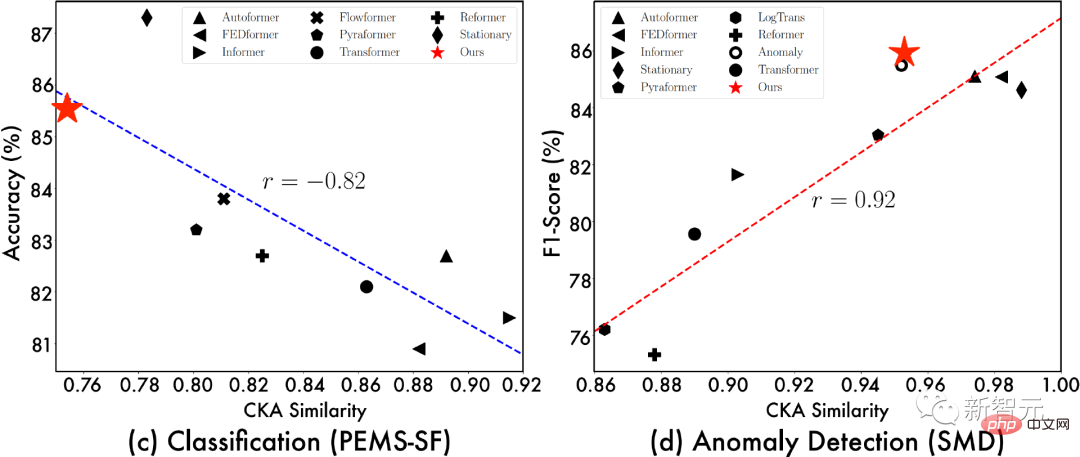
#從上述視覺化，我們可以觀察到：

• 在預測與異常檢測任務中，效果越好的模型往往底層-頂層的表徵相似度越高，表示任務需要更加底層的表徵（low-level representations）；
• #在分類與缺失值填補任務中，效果越好的模型往往底層-頂層的表徵相似度越低，顯示該任務需要層次化表徵（hierarchical representation），也就是更好的全局特徵提取能力。

得益於2D空間中的捲積操作，TimesNet可以根據不同任務學習適當的表徵，例如預測與異常檢測任務中，學習到低層次表徵；而分類與缺失值填補任務中，學習到層次化的抽象特徵。這也進一步證明了TimesNet作為基礎模型的任務泛化性。

同時，上述表徵分析也為針對專一任務的深度模型提供了設計思路，​​例如對於預測任務要關注底層細粒度特徵的提取，對於填補任務則需要進一步兼顧全局表徵的學習。

5 總結

受時間序列本質的多重週期屬性啟發，本文提出了一個任務通用的時序分析基礎模型－TimesNet。此模型創新地將一維時間序列折疊至二維空間，並利用2D卷積取時序特徵。這項創新使得時序分析任務可以直接受益於蓬勃發展的視覺骨幹網絡，對於後續研究具有良好的啟發性。

同時，TimesNet在長時、短時預測、缺失值填補、異常檢測、分類五大主流時序分析任務上實現了全面領先，具有優秀的應用價值。

以上是時序分析五邊形戰士！清華提出TimesNet：預測、填補、分類、偵測全面領先的詳細內容。更多資訊請關注PHP中文網其他相關文章！