P/NP 問題是計算複雜度領域至今未解決的問題。人們一直試圖找到一個問題的答案:「我們能否在合理時間內有效解決所有的計算問題?」
什麼是合理的時間?實際上在宇宙終結之前能夠解決的問題都算在合理時間內。然而許多問題似乎都難以在合理的時間內解決,這需要用數學來證明這些問題的難度。
2021 年的一項研究解答了上述問題,研究證實:很大一部分問題都很難有效解決。
華盛頓大學的Paul Beame 評價這項研究表示:「就像攀登山峰一樣,這項研究是計算理論研究路上的一個落腳點。」

該研究的三位研究者:電腦科學家Srikanth Srinivasan(左)、Nutan Limaye(右上)和Sébastien Tavenas。
該研究考慮的問題只涉及加法和乘法,但當這些問題僅限於以特定方式(加法和乘法的某種交替模式)解決時,它們就變得非常困難。
令人驚訝的是,該研究沒有使用新的框架或工具,相反,作者設法繞過了由普林斯頓高等研究院數學學院教授Wigderson 與耶路撒冷希伯來大學Noam Nisan 合作數十年的工作中所描述的數學障礙。
研究者之一、丹麥奧胡斯大學的Srikanth Srinivasan 說:「我們意識到有一種非常簡單的方法可以繞過這個障礙。並且,如果用這麼簡單的方法就能做到我們認為不可能的事情,那麼肯定能找到更好的方法。」
重要的問題
計算機出現之後,科學家發現計算機演算法可以解決許多問題,但有時這些演算法花費的時間太長——比實際計算時間更長。
他們開始懷疑有些問題是本質上難度太大,無論問題的規模是大是小都難以解決。例如在圖中,一個重要的問題是確定是否存在一條哈密頓路徑,即存在一條路徑通過且僅通過每個頂點一次。增加點(和邊)的數量應需要更長的時間來確定是否存在這樣的路徑,但即便是最好的演算法,隨著圖規模的增加,花費的時間也會呈指數增長,這使得解決這個問題變得不切實際。

電腦科學家試圖證明,任何能夠以某種方式有效解決某類問題中一個難題的演算法,都可以轉化為對其他類似困難問題的解決方法,他們稱這一類問題為NP 問題。
當然,也有很多看起來不難的問題,不需要花太多時間來解決。這些問題中的許多在某種意義上也是等價的,這類問題被稱為 P 問題。他們認為 NP 問題確實比 P 問題更難,並且 NP 問題永遠無法有效解決。但如果沒有證據,這種想法就可能是錯的。
因此,電腦科學家開始尋找方法來證明 NP 問題確實更難,這需要證明 NP 問題必須要指數級的時間才能解決,但證明這一點並不容易。
多難才算「難(hard)」?
設想一組只需要加法和乘法的特定問題。例如,給定一組點,可以只透過加法和乘法,用關於點的資料來計算所有可能的哈密頓路徑(如果存在的話)。
隨著問題規模的增加,一些算術問題(如計算哈密頓路徑)需要更多的時間。 1979 年,哈佛大學的 Leslie Valiant 證明許多算術問題在「難度」上是等價的,而其他的則在「沒有難度」上是等價的。計算機科學家後來以他的名字命名這兩類問題——分別是 VNP 和 VP。
和P 與NP 問題一樣,我們無法證明VNP 問題的難度,我們只知道VNP 問題比NP 問題更難,因為它建立在後者的基礎之上,例如計算路徑首先需要確定路徑是否存在。
「這比 NP 難,因此證明這很困難應該更容易」,Shpilka 說。
在隨後的幾十年中,電腦科學家在VP 與VNP 問題上取得的進展比他們在P 與NP 問題上取得的進展要大得多,但其中大部分僅限於Valiant 創建的稱為代數複雜性的子領域。在 Limaye、Srinivasan 和 Tavenas 最近的工作之前,他們仍然很難判斷是否存在一般意義上的算術問題。
調整多項式
這項新工作有助於探究電腦科學家思考加法和乘法問題的方式。從數學上講,這些問題完全可以寫多項式的形式(例如 x^2 5y 6),這些多項式由相加和相乘的變數組成。
對於任何特定問題,例如計算哈密頓路徑,你可以建立一個表示它的多項式。例如你可以用一個變數來表示每個點和邊,這樣當加入更多點和邊時,就可以在多項式中加入更多變數。
為了證明計算哈密頓路徑這樣的算術問題很困難,就需要證明當增加更多點和邊時,相應的多項式需要以指數時間解決更多操作。例如,x^2 需要一次操作(x * x),而 x^2 y 需要兩次操作(x * x 然後加上 y)。操作的數量稱為多項式的大小。
但是多項式的大小很難確定。例如多項式 x^2 2x 1。它的大小似乎為4(兩次乘法和兩次加法),但是該多項式可以重寫為兩個和的乘積,(x 1)(x 1),它的操作數更少-兩次加法,一次乘法。通常,隨著問題的規模擴大和將更多變數添加到多項式中,數學變換可以幫助簡化和縮小其規模。
在 Valiant 的研究幾年之後,電腦科學家找到了一種方法,可以讓問題的大小更易於分析。為此,他們提出了一個稱為「深度(depth)」的屬性,它指定多項式在和與乘積之間切換或交替的次數。例如,多項式 x^2 2x 1 的深度為 2,因為它是乘積總和(如 x^2 和 2x)。相較之下,表達式 (x 1)(x 1) 的深度為 3,因為它的深度與 0 (x 1)(x 1) 相同,依照乘積總和計算。

為了簡化多項式,電腦科學家將它們限制為一種固定形式,並具有稱為「恆定深度」的屬性,其中和、乘積的模式不會隨著問題的成長而改變。這使得它們的大小更加固定,多項式的大小會隨著其深度的增加而減少。某個恆定深度的表達式稱為公式。恆定深度讓多項式的研究有更多進展。
神奇的「深度」
1996 年, Nisan 和 Wigderson 的一篇論文專注於解決矩陣乘法的問題,他們用兩種方式簡化了這個問題。首先,他們用恆定深度的公式來表示它——深度為 3。其次,他們只考慮了具有某種簡單結構的公式,其中每個變數的最大指數為 1,這使得原始問題成為「多線性」問題。
電腦科學家已經發現,某些問題可以轉換為相對簡單的集合多線性(set-multilinear)結構,代價是多項式的大小呈次指數增長(與指數增長的增長率相當)。
Nisan 和 Wigderson 隨後顯示了隨著矩陣的擴大,矩陣乘法問題需要指數級的時間來解決。換句話說,他們證明了一個重要的問題是困難的,為證明一類問題都是困難的做出了努力。然而,他們的結果只適用於具有簡單的、集合多線性結構的公式。

Leslie Valiant
增加多項式的深度往往會導致其大小減少。隨著時間的推移,電腦科學家使這兩個屬性之間的權衡變得更精確。他們表明,將兩個深度等級添加到深度 3、集合多線性多項式可以平衡其集合多線性結構的大小增益。如果深度 5 的結構化公式需要指數時間,那麼具有一般、非結構化性質的深度 3 公式也是如此。
Srikanth Srinivasan 等人的新工作表明,矩陣乘法問題的深度 5 集合多線性公式確實以與指數級速度增長。這意味著一般的深度 3 公式也需要指數時間。隨後他們證明類似的規律適用於所有深度(不只 3 和 5)。有了這種關係,他們就證明了對於同一個問題,任何深度的一般公式的大小都會隨著問題的規模而以指數速度增長。
他們也顯示用一個恆定深度的公式表示矩陣乘法是很難的,無論該深度是多少。
該研究的結果首次提供了對於算術問題何時是「困難」的一般理解——當它不能用恆定深度的公式表示時即為困難。矩陣乘法的具體問題已知是 VP 問題。且已知 VP 問題在不限於恆定深度時相對容易,因此結果得出恆定深度為問題「困難」的來源。
VNP 問題是否比 VP 問題更難?新結果並沒有直接說明這一點,他們只顯示恆定深度公式很難。但這仍然是證明 VNP 問題不能等價於 VP 問題的重要里程碑。
對於更大的 P 與 NP 問題,我們現在可以對有一天能找到答案更加樂觀了。畢竟為了解決困難的問題,我們首先需要知道哪些方向是無望的。
以上是如何證明一個問題是VNP問題?計算機科學家找到了一種簡單方法的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 如何使用LM Studio在本地運行LLM? - 分析VidhyaApr 19, 2025 am 11:38 AM
如何使用LM Studio在本地運行LLM? - 分析VidhyaApr 19, 2025 am 11:38 AM輕鬆在家運行大型語言模型:LM Studio 使用指南 近年來,軟件和硬件的進步使得在個人電腦上運行大型語言模型 (LLM) 成為可能。 LM Studio 就是一個讓這一過程變得輕鬆便捷的優秀工具。本文將深入探討如何使用 LM Studio 在本地運行 LLM,涵蓋關鍵步驟、潛在挑戰以及在本地擁有 LLM 的優勢。無論您是技術愛好者還是對最新 AI 技術感到好奇,本指南都將提供寶貴的見解和實用技巧。讓我們開始吧! 概述 了解在本地運行 LLM 的基本要求。 在您的電腦上設置 LM Studi
 蓋伊·佩里(Guy Peri)通過數據轉換幫助麥考密克的未來Apr 19, 2025 am 11:35 AM
蓋伊·佩里(Guy Peri)通過數據轉換幫助麥考密克的未來Apr 19, 2025 am 11:35 AM蓋伊·佩里(Guy Peri)是麥考密克(McCormick)的首席信息和數字官。儘管他的角色僅七個月,但Peri正在迅速促進公司數字能力的全面轉變。他的職業生涯專注於數據和分析信息
 迅速工程中的情感鍊是什麼? - 分析VidhyaApr 19, 2025 am 11:33 AM
迅速工程中的情感鍊是什麼? - 分析VidhyaApr 19, 2025 am 11:33 AM介紹 人工智能(AI)不僅要理解單詞,而且要理解情感,從而以人的觸感做出反應。 這種複雜的互動對於AI和自然語言處理的快速前進的領域至關重要。 Th
 12個最佳數據科學工作流程的AI工具-Analytics VidhyaApr 19, 2025 am 11:31 AM
12個最佳數據科學工作流程的AI工具-Analytics VidhyaApr 19, 2025 am 11:31 AM介紹 在當今以數據為中心的世界中,利用先進的AI技術對於尋求競爭優勢和提高效率的企業至關重要。 一系列強大的工具使數據科學家,分析師和開發人員都能構建,Depl
 AV字節:OpenAI的GPT-4O Mini和其他AI創新Apr 19, 2025 am 11:30 AM
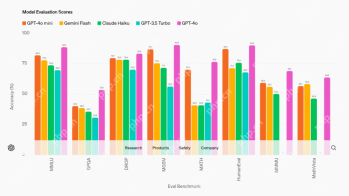
AV字節:OpenAI的GPT-4O Mini和其他AI創新Apr 19, 2025 am 11:30 AM本週的AI景觀爆炸了,來自Openai,Mistral AI,Nvidia,Deepseek和Hugging Face等行業巨頭的開創性發行。 這些新型號有望提高功率,負擔能力和可訪問性,這在TR的進步中推動了
 報告發現,困惑的Android應用程序有安全缺陷。Apr 19, 2025 am 11:24 AM
報告發現,困惑的Android應用程序有安全缺陷。Apr 19, 2025 am 11:24 AM但是,該公司的Android應用不僅提供搜索功能,而且還充當AI助手,並充滿了許多安全問題,可以將其用戶暴露於數據盜用,帳戶收購和惡意攻擊中
 每個人都擅長使用AI:關於氛圍編碼的想法Apr 19, 2025 am 11:17 AM
每個人都擅長使用AI:關於氛圍編碼的想法Apr 19, 2025 am 11:17 AM您可以查看會議和貿易展覽中正在發生的事情。您可以詢問工程師在做什麼,或諮詢首席執行官。 您看的任何地方,事情都以驚人的速度發生變化。 工程師和非工程師 有什麼區別
 火箭發射模擬和分析使用Rocketpy -Analytics VidhyaApr 19, 2025 am 11:12 AM
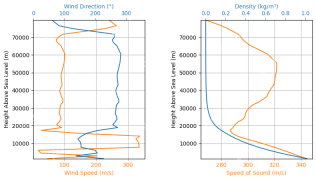
火箭發射模擬和分析使用Rocketpy -Analytics VidhyaApr 19, 2025 am 11:12 AM模擬火箭發射的火箭發射:綜合指南 本文指導您使用強大的Python庫Rocketpy模擬高功率火箭發射。 我們將介紹從定義火箭組件到分析模擬的所有內容


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

PhpStorm Mac 版本
最新(2018.2.1 )專業的PHP整合開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

SAP NetWeaver Server Adapter for Eclipse
將Eclipse與SAP NetWeaver應用伺服器整合。

EditPlus 中文破解版
體積小,語法高亮,不支援程式碼提示功能

DVWA
Damn Vulnerable Web App (DVWA) 是一個PHP/MySQL的Web應用程序,非常容易受到攻擊。它的主要目標是成為安全專業人員在合法環境中測試自己的技能和工具的輔助工具,幫助Web開發人員更好地理解保護網路應用程式的過程,並幫助教師/學生在課堂環境中教授/學習Web應用程式安全性。 DVWA的目標是透過簡單直接的介面練習一些最常見的Web漏洞,難度各不相同。請注意,該軟體中






