人类在成长过程的不同阶段均需要掌握很多的知识点来求解大量的数学题。然而,知识点看懂了不算真的懂,能求解题目才能体现人类的智慧。近年来,神经网络在计算机视觉,模式匹配、自然语言处理、强化学习等领域取得了巨大成功,但神经网络模型的离散组合推理能力远不及人类。那么,神经网络能否理解数学题,并解出这些题目呢?如果可以,那么神经网络的解题能力如何?
从数据形式上来说,一道数学题可以看作是一个序列,而其解答(解题步骤或者求解表达式)往往也是以序列的形式呈现。那么数学题求解可以看作是从自然语言到数学语言的翻译问题,神经网络模型从形式上能求解数学问题。从前人的各种研究工作中可以获知,神经网络能在翻译问题上获得很好的性能,并在多个数据集上获得了超越了人类的性能。然而,与机器翻译显著不同,除了题目语义理解能力之外,数学题求解往往还需要模型具备对代数泛化对象和实体的离散组合推理能力。
为了探究深度模型对数学题的解题能力,中山大学人机物智能融合实验室在前人研究的基础上以中小学数学应用题和几何计算题为切入点,开展了一系列研究,改进了深度模型的语义理解、认知推理和数学解题能力。本文将对中山大学人机物智能融合实验室在数学解题领域的一系列研究进行简要介绍。
论文1:Semantically-Aligned Universal Tree-Structured Solver for Math Word Problems

The 2020 Conference on Empirical Methods in Natural Language Processing
论文地址:https://aclanthology.org/2020.emnlp-main.309.pdf
一个实用的数学应用题求解器应该能够解决各种类型的数学应用题,如一元一次方程,二元一次方程组,一元二次方程等类型。然而,大多数的数学应用题求解工作只针对四则运算类题目进行设计,而这类设计往往难以扩展到更多题型,无法使用一个统一的数学应用题求解器同时求解各种类型表达式的应用题。此外,当下的大部分数学应用题求解器缺乏对题目文本和求解表达式之间的语义约束。
针对上述问题,中山大学人机物智能融合实验室团队提出一种统一表达式树表示方案,通过引入额外的运算符连结多个表达式,将一元一次方程,二元一次方程组,一元二次方程等类型的表达式进行统一表示,从而可以简化求解器的设计的同时也可以求解多种类型的应用题,如图 1 所示。

图 1 统一表达式树表示方案设计
基于统一表达式树表示方案,我们进而提出了一种语义对齐的树结构通用求解器(SAU-Solver),如图 2 所示。我们的树结构通用求解器由两部分组成,基于双层 GRU 的问题编码器和基于统一表达式树表示的树结构解码器。并且在训练过程中,我们引入了语义对齐正则化,通过约束表达式子树与题目上下文的一致性使得我们的通用求解器能更充分地考虑问题和表达式之间的语义关系,发掘各类数学知识,从而提升求解器的表达式生成能力。

图 2 语义对齐树结构求解器
此外,為了更好地衡量求解器的通用性和求解能力,我們還針對當前標註資料集中題型種類單一的問題,構建了一個中等規模的多題型資料集HMWP,該資料集包括了求解表達式為一元一次方程,二元一次方程組,一元二次方程等多種表達式類型的數千道數學文字題目。我們的實驗表明,具有多題型的資料集比種類單一的資料集對求解器來說更具有挑戰性,也能更好地衡量求解器的解題能力,推動求解器社群的研究。
在實驗中,文章將提出的 SAU-Solver 與現有方法在 HMWP、Math23K、ALG514 和 Dolphin18K-Manual 進行了對比。實驗結果如下圖所示,證明了我們方法的通用性和更好的數學解題能力。

更多研究細節,可參考原文。
論文2:Neural-Symbolic Solver for Math Word Problems with Auxiliary Tasks

#The 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing

############################論文地址:https://arxiv.org/abs/2107.01431###############目前的初等數學應用題求解器沒有考慮各種數學符號約束,而是只是簡單地使用編碼器- 解碼器框架進行求解的問題,從而導致了不合理的預測。而引入符號限制和符號推理對於數學應用題自動求解是非常關鍵的。 ############因此,中山大學人機物智慧融合實驗室團隊引入神經- 符號運算範式,提出新型的神經- 符號解算器(NS-Solver),以輔助任務的方式進行顯式的知識注入,從而實現不同層級的符號限制。其技術架構如圖 3 所示。 NS-Solver 在網路骨幹上由三個組件建構:1)Problem Reader,透過雙層雙向GRU 網路對數學題進行高效的語義理解和表示;2)Programmer,負責基於問題語義以及常識預測結果進行符號推理,產生求解表達式。 3)Executor,利用 sympy 函式庫進行表達式求解,取得最終答案。 ############在符號限制上,我們提出多種輔助任務來利用額外的訓練訊號和利用常識預測結果來明確地約束符號表,降低問題求解搜尋空間:1)自監督的數字預測任務:透過預測題目中數字的位置和數量來更好地理解題目語義;2)常識量詞預測任務:注入常識知識並利用預測結果約束符號表,降低搜尋空間;3)一致性檢視:從語意層面檢視解題器的輸出與目標表達式的一致性;4)對偶利用任務:透過問題到表達式和表達式到問題的雙向約束,強化解題器的問題語意理解。 ###########################圖3 神經- 符號解算器(NS-Solver)########### #######此外,為了更好地驗證求解器的效能,我們也建構了一個更大規模的多題型數學應用題資料集CM17K,以便更好地推動數學解題社群的研究。 CM17K 包含了 6215 道四則運算類應用題,5193 道一元一次方程類應用題,3129 道一元非線性方程類應用題和 2498 道方程組類應用題。 CM17K 和 Math23K 的資料統計如下表所示。從數據統計上可以看出,CM17K 相比Math23K 具有更長的題目信息,更長的求解表達式,涉及更多的常識等,這意味著CM17K 在求解難度上更好地刻畫解題器的性能。 ######

在實驗中,文章將提出的NS-Solver 與現有方法在Math23K 和CM17K 上進行了對比,並進行了消融實驗,證明了NS-Solver良好的解題能力和通用性。其實驗結果如下面兩個表所示。

此外,我們也對輔助任務進行了消融實驗,如下圖所示。實驗結果證明了各個輔助任務都能提升 NS-Solver 的解題能力。

更多研究細節,可參考原文。
論文3:GeoQA – A Geometric Question Answering Benchmark Towards Multimodal Numerical Reasoning

#Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021
論文網址:https://arxiv .org/pdf/2105.14517.pdf
#自動數學解題最近獲得了越來越多的關注。自動數學解題大多數工作關注數學應用題自動求解。然而很少工作關注幾何題。相比較於數學應用題,幾何題需要同時對文字描述、圖形圖表來理解,因為在幾何題目中,題目文字和圖形圖表通常是相輔相成,缺一不可的。現有的幾何題自動求解方法高度依賴規則並且只在小資料集上進行評估。

圖4 幾何問題範例
為了推動幾何題自動求解的研究,中山大學人機物智慧融合實驗室團隊建構了一個由5010 道幾何選擇題組成的問答資料集GeoQA。如圖 4 所示,GeoQA 資料集中的每個樣本具有題目描述、幾何影像、問題選項、答案、問題類型、知識點、解答解析,以及依解題步驟標註的形式程序。在題目規模上,此資料集是前人工作常用的 GeoS 資料集的 25 倍。 GeoQA 資料集的相關統計資料如下表所示。

而 GeoQA 資料集所使用的形式程式運算子和所涉及的常數如下表所示。

為了更好地促進幾何題求解器的研究,我們除了在GeoQA 資料集的基礎上建立了一些基準模型外,還提出了神經幾何題求解器NGS 來理解多模態語義資訊並產生具有解釋性的形式化程序。神經幾何題求解器 NGS 的整體設計如圖 5 所示。

###########################################
我們的 NGS 主要由文字編碼器、幾何圖形編碼器,聯合推理模組和程式解碼器組成。文字編碼器負責對題目文字語意表徵,幾何圖形編碼器則負責幾何圖形的表徵。文字表徵和圖形表徵都會輸入到聯合推理模型進行多模態語意表徵,並投餵到程式解碼器中進行程式解碼,輸出可解釋可執行的形式化解程式。
此外,為了增強幾何圖形編碼器對幾何圖形的表徵能力以及推進聯合推理模組對題目所包含的多模態信息進行充分融合和高效表達,我們還引入了多種輔助任務來改善模型的表徵能力和注入定理知識。這些輔助任務包括:1)拼圖位置預測:透過將幾何圖形切割為多個patch,並隨機排列,然後讓幾何圖形編碼器對其重新排列,實現對幾何圖形的像素級圖形理解;2)幾何元素預測:讓幾何圖形編碼器學習預測哪些幾何元素出現在了當前的幾何圖形中,實現對象級圖形理解;3)知識點預測:在聯合推理模組進行題目文本表徵和幾何圖形表徵的多模態融合的同時引入知識點分類任務來改進整體的問題表徵。在 NGS 中,我們利用拼圖位置預測和幾何元素預測對幾何圖形編碼器進行預先訓練。而知識點預測任務則作為一個子任務和 NGS 進行多任務訓練。
在實驗中,文章基於 GeoQA 建立了多個基於神經網路的基準模型,並將 NGS 與他們進行比較。 NGS 和基準模型在 GeoQA 上的實驗效果如下表所示。

從上表可以看到,NGS 相比基準模型在 GeoQA 上能達到更好的解題效能。但我們也可以看到各類模型與人類在幾何題求解上仍有較大的差距。
此外,我們也進行了各種消融實驗,驗證了 NGS 中各種設計的有效性。更多研究細節,可參考原論文。
論文4:Unbiased Math Word Problems Benchmark for Mitigating Solving Bias

Findings of the Association for Computational Linguistics: NAACL 2022
論文地址:https://aclanthology.org/2022 .findings-naacl.104.pdf
在這個工作中,中山大學人機物智能融合實驗室團隊重新審視在當前的數學應用題求解基準上評估模型的解題偏壓(solving bias)。這種解題偏壓主要資料偏移(data bias)和學習偏壓(learning bias)所引起。資料偏移(data bias)是指訓練資料集未能涵蓋每個問題的所有不同敘述方式而導致的解題模型只能學習到淺層語義,未能對題意進行深度語義理解的問題,如圖6(a)所示,由於解題模型只學習到淺層語義,並以此來進行解題, 那麼即使我們把題目中的問題部分移除後,解題器仍然能達到69.4%。
而學習偏移則是指一個MWP 可以由多個等價的表達式來求解,但是目前的資料集皆只採用其中某一個等價方程式作為標籤,強制模型學習該標籤,而忽略了其他等價方程,導致學習訓練的偏移。如圖6(b)所示,在訓練過程中,模型可能會產生與GroundTruth 表達式不一致但是答案是正確的表達式,但是由於資料集只採用了某一等價表達式作為標籤,會導致在計算損失函數時認為該表達式是錯誤表達式,並將兩個正確表達式之間的損失反向傳播給求解模型,導致了模型的過度矯正。

圖 6 資料偏移與學習偏移的範例
為了緩解資料偏移(data bias),中山大學人機物智慧融合實驗室團隊作了一個新的嘗試,我們以盡可能涵蓋題目問法的方式重新標註了一個新的MWP基準UnbiasedMWP。我們收集了 2907 到應用題作為基礎問題,然後我們為每個問題中所蘊涵的故事標註盡可能多的問題。
為了簡化人工標註過程,我們先根據題目骨幹的內容產生一些合理的表達式,然後再反向重寫問題。為了產生合理的表達式,我們設計了三種表達式變種方式:1)Variable assortment (Va) 變形:從題目骨幹隨機選擇兩個數字變量,並使用數學運算符( 、-、*、/)對他們進行組合,例如n0 n1, n0 − n1 等。 2)Subexpression (Sub) 變形:原題目的目標表達式所蘊含的所有子表達式是運算子的修改,從而得到新的表達式。 3)Whole-expression (Whole)變形:透過改變原題目的目標表達式所包含的運算子來取得新的表達式。對於從上述三個變種取得所得的新表達式集合進行人工過濾,過濾出無法進行新問題標註的表達式,對剩餘表達式進行人工問題標註。
為了緩解學習偏移(learning bias),我們提出動態目標選擇策略,在訓練過程中根據模型輸出的結果來選擇與其更加接近的目標表達式來作為GroundTruth 。為了得到等價的表達式,我們利用數學運算中的交換律來對表達式樹進行變形,從而獲得多個等價的表達式。如圖 7 所示。

圖7 等價表達式樹產生示意圖
在實驗中,文章首先在多個SOTA 基準模型上對UnbiasedMWP 資料集進行驗證。其實驗結果如下表所示。

從實驗結果可以看到,相較於現存的Math23K,我們的資料集UnbiasedMWP 所存在的資料偏移較少,因為當我們移除了題目問題後,模型的求解性能急劇下降,從側面證明了我們的資料集更能使得模型需要關注深層語意資訊才能進行求解。
為了驗證我們的動態目標選擇策略是否能降低學習偏置,我們將動態目標選擇策略應用在多個解題模型上。實驗結果如下表所示。

從實驗結果可以看到,我們的動態目標選擇策略能有效地降低學習偏置,並提升了模型的求解效果。更多研究細節,可參考原論文。
論文5:LogicSolver: Towards Interpretable Math Word Problem Solving with Logical Prompt-enhanced Learning

#Findings of the Association for Computational Linguistics: EMNLP 2022
論文網址:https:// arxiv.org/pdf/2205.08232.pdf
近年來,深度學習模型在數學應用問題自動求解任務上取得了很大的成功,特別是在答案準確率方面。但由於這些模型只利用了統計線索(shallow heuristics)實現了高求解性能,並沒有真正地理解和推理題目背後的數學邏輯,因此,這些方法是難以解釋的。
為了解決該問題並推動可解釋數學應用題求解領域的發展,中山大學人機物智能融合實驗室團隊構建了第一個高質量的帶解釋的數學應用題數據集 InterMWP。此資料集包含了 11,495 道數學應用題和 210 種基於代數知識的邏輯公式,每道應用題的解算式均使用邏輯公式進行標註。與現有的數學應用題求解資料集不同,我們的InterMWP 不僅要求解題器輸出求解表達式,還要求解題器輸出該求解表達式所對應的基於代數知識的邏輯表達式,從而實現對模型輸出的解釋。 InterMWP 資料集與其他解題資料集的異同可以參考圖 8。具體的標註過程可以參考原文。

圖8 InterMWP 資料集範例
為了利用數學邏輯知識並賦能MWP 解題器具備可解釋性,我們團隊進一步地建構了新的數學應用題求解框架LogicSolver,如圖9 所示。該框架透過檢索的方式從邏輯公式庫提取相關的邏輯知識作為提示訊息,改進問題編碼器對 MWP 的語義表示的同時增強 MWP 的邏輯解釋的生成能力。


LogicSolver 主要由邏輯知識檢索元件、邏輯提示增強MWP 求解器、解釋產生元件三大元件所構成。邏輯知識檢索元件。對於每一道 MWP,我們從 210 個邏輯公式檢索 top-k 個高度相關的邏輯公式作為提示,以增強 MWP 的解。我們將邏輯公式提示與問題文字連接起來作為輸入,驅動 MWP 模型產生求解表達式。最後,為了獲得基於邏輯公式的解釋,我們部署一個邏輯產生器來預測邏輯表達式樹的每個內部節點(即運算子)所對應的邏輯公式作為求解的解釋。 在實驗中,我們在 InterMWP 資料集上建立了多個基準模型,並將我們的 LogicSolver 與這些基準模型進行比較。其實驗結果如下表所示。
###從實驗結果可以看出,我們的LogicSolver 在答案準確度,公式準確率,以及邏輯公式準確度上都能獲得提升,說明了我們的LogicSolver 在改善求解性能(Answer Acc 和Formula Acc)的同時能具有更好的邏輯解釋性(Logic Acc)。更多研究細節,可參考原論文。 ###############論文6:UniGeo: Unifying Geometry Logical Reasoning via Reformulating Mathematical Expression##################Jiaqi Chen, Tong Li, Jinghui Qin, Pan Lu, Liang Lin, Chongyu Chen and Xiaodan Liang#####################The 2022 Conference on Empirical Methods in Natural Language Processing### ###############幾何題自動求解是用來評估深度模型多模態推理能力的基準。然而,在大多數現有的工作中,幾何計算題自動求解和幾何題自動證明通過會被視作兩個不同的任務,並施加不同的標註處理,妨礙了深度模型在不同數學任務進行統一推理的研究進展。從本質上來說,幾何計算題和幾何證明題目具有相似的問題表達和解題所需的數學知識也有所重疊。因此,透過對幾何計算題自動求解和幾何題自動兩個任務進行統一表示和學習有助於提升深度模型對這兩種問題的語義理解和符號推理。 ######
為此,中山大學人機物智慧融合實驗室團隊建構了一個包含了數千道幾何題的基準資料集 UniGeo。 UniGeo 包含了 4,998 道幾何計算題和 9,543 個幾何證明。我們對每個證明題均進行了多步驟證明標註,而這些標註可以很輕易地被轉換為可執行的符號程序。而計算題也採用類似的標註,如圖 10 所示。經過採用如圖 10 所示的方式進行標註後,UniGeo 能很好地以形式化符號語言將幾何計算題和幾何證明題進行統一的表示。

圖10 UniGeo 資料範例

圖11 GeoFormer 示意圖
 ##此外,為了習得高效的Geoformer 實現統一的幾何推理,中山大學人機物智能融合實驗室團隊也進一步地提出數學表達預訓練任務,結合MLM 任務對Geoformer 進行任務預訓練,如圖12 所示。
##此外,為了習得高效的Geoformer 實現統一的幾何推理,中山大學人機物智能融合實驗室團隊也進一步地提出數學表達預訓練任務,結合MLM 任務對Geoformer 進行任務預訓練,如圖12 所示。

##在實驗中,我們在UniGeo 基準的基礎上建立多個基準模型,並對我們提出的GeoFormer 進行效能比較。實驗結果如下表所示。

從實驗結果可以看到,我們提出的GeoFormer 在計算題和證明題兩個子資料集上均能獲得比基準模型更好的整體性能。類似地,在需要統一求解計算題和證明題的全資料集上 GeoFormer 相比 NGS 和 BERT 基線模型也是更優勝的。而經過數學表現預訓練和 MLM 預訓練後,GeoFormer Pretraining 相比 GeoFormer 會有進一步的表現提升。這些實驗結果充分證明了 GeoFormer 的有效性,也說明了對幾何計算題和幾何證明題進行統一模型推理對於各自的任務來說也是有幫助的。 該工作已被 EMNLP2022 主會收錄,更多研究細節,更多細節敬請期待。
######論文7:Template-based Contrastive Distillation Pre-training for Math Word Problem Solving###################Jinghui Qin*, Zhicheng Yang*, Jiaqi Chen, Xiaodan Liang and Liang Lin###############雖然深度學習模型在數學解題領域取得很好的進展,但是這些模型忽略了蘊涵在問題描述中的求解邏輯,而這個解題邏輯往往可以和解題模板(解法)相對應。如圖 13 所示,兩個不同的應用題都可以對應相同的解法。 ###########################圖13 語言描述不同但解法相同的應用問題範例########### #此外,預訓練語言模型 (PLM) 包含豐富的知識和擁有高品質語義表示的能力,這對於 MWP 問題的求解會有幫助。
為了充分利用預訓練語言模型所包含的豐富知識以及利用求解邏輯來更有效率地求解應用題,中山大學人機物智能融合實驗室團隊提出基於解法模板和預訓練語言模型的對比蒸餾預訓練方法對求解器中的問題編碼器進行領域預訓練,如圖14 所示。該方法使用多視角對比學習有效地考慮數學邏輯知識的同時利用知識蒸餾的方式有效地保留了預訓練語言模型中的知識和高質量語義表示能力。
具體來說,我們先以兩題目之間的解法模板是否一致來作為判定兩題目是否應該在表示空間上互相靠近的標識。然後,我們提出多視角對比學習,從教師編碼器以及學生編碼器及其對應的Momentum 編碼器進行對比學習,使得兩道具有相同解法模板的題目表示在教師表示空間中和學生表示空間中進行互相靠近,從而實現解法邏輯的注入。此外,為了盡可能保留以預訓練語言模型進行初始化的學生編碼器中所蘊涵的知識和高品質表示能力,我們使用知識蒸餾,利用教師編碼器的特徵表示作為監督,約束學生編碼器的表示要與已訓練好的教師編碼器具有相同的表示能力,從而實現語義保持。

圖14 基於解法模板和預訓練語言模型的對比蒸餾預訓練方法
在實驗中,我們使用不同的預訓練語言模型作為初始化並驗證我們方法的效果。我們分別使用 BERT-base 和 Roberta-base 權重對問題編碼器 MathEncoder 進行初始化,並使用 GTS 中的 decoder 作為表達式解碼器。我們統稱基於 MathEncoder 的求解器為 MathSolver。我們將 MathSolver 與多個方法在 Math23K 和 CM17K 上進行了比較。實驗結果如下表所示。


從實驗結果可以看到,我們所提出的方法能有效地提升求解器的解題能力,並能在多種不同的預訓練語言模型上進行應用。成果已投稿至 IEEE Transactions on Neural Networks and Learning Systems,更多細節敬請期待。
論文8:An Introspective Data Augmentation Method for Training Math Word Problem Solvers
Jinghui Qin, Zhongzhan Huang, Ying Zeng, and Liang Lin
#近年來,越來越多的研究者開始研究基於深度學習的方法進行數學應用題自動求解,因為數學應用題自動求解能充分展現機器智能的程度。因為標註高品質大規模的MWP 資料集的代價很高,例如需要相應教育程度的專業知識和大規模可存取的題目數據,所以現有的高品質MWP 資料集的規模對於訓練一個高效的MWP 解題器是遠遠不夠的。
MWP 的資料瓶頸問題鼓舞我們思考如何使用成本高效的資料增強方法來改善資料利用效率,提升求解器的效能。最直接的資料增強方法就是基於輸入的資料增強方法,如常用的字元替換,字元刪除等,但是這類方法對於MWP 來說是不適用的,因為MWP 具有言簡意賅的特點,對輸入的文字的擾動或修改容易使得題意模糊。此外,題意所蘊含的數學關係是不能被改變的,但這類方法很可能會改變題意所蘊含的數學關係,如圖 15 所示。

圖15 基於輸入的資料增強方法不適用於MWP 任務的範例
此外,中山大學人機物智慧融合實驗室團隊也對基於輸入的資料增強方法進行了一定的驗證,其實驗結果如圖16 所示。實驗結果顯示了基於輸入的明確資料增強方法對於 MWP 任務來說是不適用的,無法有效緩解 MWP 任務所遇到的資料瓶頸問題。

圖16 基於輸入的資料增強方法無法提升MWP 解題效果
為此,我們提出了一種適用於MWP 資料的簡單且有效率的資料增強方法- 自省式資料增強方法(IDAM),在訓練過程種對題目在隱空間的表示進行增強,從而解決了基於輸入的資料增強方法在MWP 求解任務上所遇到的問題。 IDAM 方法透過對問題的表示編碼執行不同的表示建構方法(均值池化、層次化聚合,隨機丟棄,隨機交換等),得到一個新的問題表示,然後使用一致性目標函數(基於表達式之間的JS 散度)來約束求解器基於新問題表示的表達式解碼輸出要和基於原問題表示的表達式解碼輸出具有一致性。此方法的示意圖如圖 17 所示。

圖17 自省式資料增強方法(IDAM)示意圖
在實驗中,我們將IDAM 嵌入到多個SOTA 方法中並在多個資料集上進行了對比,驗證了我們IDAM 方法的有效性和通用性。實驗結果如下表所示。從實驗結果可以看到,在相同的實驗配置下,我們的 IDAM 在不同的 MWP 資料集上均能對不同的求解器基準模型的效能進行提升。這充分說明了我們 IDAM 方法在 MWP 問題上的有效性。
此成果已投稿至 IEEE/ACM Transactions on Audio, Speech and Language Processing,更多細節敬請期待。
實驗室簡介
中山大學人機物智慧融合實驗室(HCP Lab)由林倞教授於2010年創辦,圍繞人工智慧前沿技術佈局研究主題,獲得中國圖像圖形學會科技一等獎、吳文俊自然科學獎、省級自然科學一等獎等榮譽;培養了梁小丹、王可澤等國家級青年人才。
以上是中山大學HCP Lab團隊:AI解題新突破,神經網路推開數學推理大門的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 閱讀AI索引2025:AI是您的朋友,敵人還是副駕駛?Apr 11, 2025 pm 12:13 PM
閱讀AI索引2025:AI是您的朋友,敵人還是副駕駛?Apr 11, 2025 pm 12:13 PM斯坦福大學以人為本人工智能研究所發布的《2025年人工智能指數報告》對正在進行的人工智能革命進行了很好的概述。讓我們用四個簡單的概念來解讀它:認知(了解正在發生的事情)、欣賞(看到好處)、接納(面對挑戰)和責任(弄清我們的責任)。 認知:人工智能無處不在,並且發展迅速 我們需要敏銳地意識到人工智能發展和傳播的速度有多快。人工智能係統正在不斷改進,在數學和復雜思維測試中取得了優異的成績,而就在一年前,它們還在這些測試中慘敗。想像一下,人工智能解決複雜的編碼問題或研究生水平的科學問題——自2023年
 開始使用Meta Llama 3.2 -Analytics VidhyaApr 11, 2025 pm 12:04 PM
開始使用Meta Llama 3.2 -Analytics VidhyaApr 11, 2025 pm 12:04 PMMeta的Llama 3.2:多模式和移動AI的飛躍 Meta最近公佈了Llama 3.2,這是AI的重大進步,具有強大的視覺功能和針對移動設備優化的輕量級文本模型。 以成功為基礎
 AV字節:Meta' llama 3.2,Google的雙子座1.5等Apr 11, 2025 pm 12:01 PM
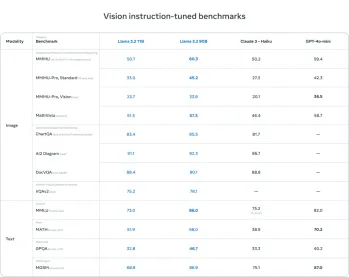
AV字節:Meta' llama 3.2,Google的雙子座1.5等Apr 11, 2025 pm 12:01 PM本週的AI景觀:進步,道德考慮和監管辯論的旋風。 OpenAI,Google,Meta和Microsoft等主要參與者已經釋放了一系列更新,從開創性的新車型到LE的關鍵轉變
 與機器交談的人類成本:聊天機器人真的可以在乎嗎?Apr 11, 2025 pm 12:00 PM
與機器交談的人類成本:聊天機器人真的可以在乎嗎?Apr 11, 2025 pm 12:00 PM連接的舒適幻想:我們在與AI的關係中真的在蓬勃發展嗎? 這個問題挑戰了麻省理工學院媒體實驗室“用AI(AHA)”研討會的樂觀語氣。事件展示了加油
 了解Python的Scipy圖書館Apr 11, 2025 am 11:57 AM
了解Python的Scipy圖書館Apr 11, 2025 am 11:57 AM介紹 想像一下,您是科學家或工程師解決複雜問題 - 微分方程,優化挑戰或傅立葉分析。 Python的易用性和圖形功能很有吸引力,但是這些任務需要強大的工具
 3種運行Llama 3.2的方法-Analytics VidhyaApr 11, 2025 am 11:56 AM
3種運行Llama 3.2的方法-Analytics VidhyaApr 11, 2025 am 11:56 AMMeta's Llama 3.2:多式聯運AI強力 Meta的最新多模式模型Llama 3.2代表了AI的重大進步,具有增強的語言理解力,提高的準確性和出色的文本生成能力。 它的能力t
 使用dagster自動化數據質量檢查Apr 11, 2025 am 11:44 AM
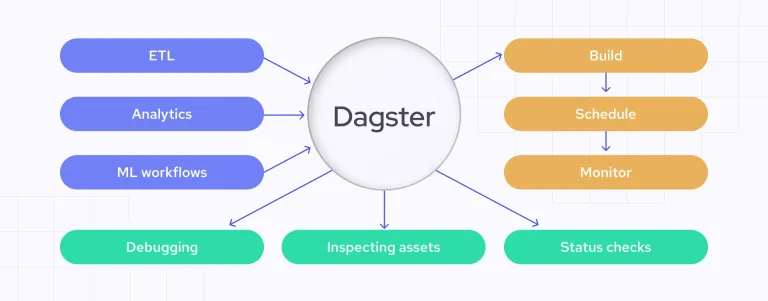
使用dagster自動化數據質量檢查Apr 11, 2025 am 11:44 AM數據質量保證:與Dagster自動檢查和良好期望 保持高數據質量對於數據驅動的業務至關重要。 隨著數據量和源的增加,手動質量控制變得效率低下,容易出現錯誤。
 大型機在人工智能時代有角色嗎?Apr 11, 2025 am 11:42 AM
大型機在人工智能時代有角色嗎?Apr 11, 2025 am 11:42 AM大型機:AI革命的無名英雄 雖然服務器在通用應用程序上表現出色並處理多個客戶端,但大型機是專為關鍵任務任務而建立的。 這些功能強大的系統經常在Heavil中找到


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

EditPlus 中文破解版
體積小,語法高亮,不支援程式碼提示功能

SublimeText3 Linux新版
SublimeText3 Linux最新版

WebStorm Mac版
好用的JavaScript開發工具

禪工作室 13.0.1
強大的PHP整合開發環境

Atom編輯器mac版下載
最受歡迎的的開源編輯器





