解決VAE表示學習問題,北海道大學提出新型生成模式GWAE
- 王林轉載
- 2023-04-07 17:47:331904瀏覽
學習高維度資料的低維表示是無監督學習中的基本任務,因為這種表示簡潔地捕捉了資料的本質,並且使得執行以低維輸入為基礎的下游任務成為可能。變分自編碼器(VAE)是一種重要的表示學習方法,然而由於其目標控製表示學習仍然是一個具有挑戰性的任務。雖然 VAE 的證據下界(ELBO)目標進行了生成建模,但學習表示並不是直接針對該目標的,這需要對錶示學習任務進行特定的修改,如解糾纏。這些修改有時會導致模型的隱式和不可取的變化,使得控製表示學習成為一個具有挑戰性的任務。
為了解決變分自編碼器中的表示學習問題,本文提出了一種稱為 Gromov-Wasserstein Autoencoders(GWAE)的新型生成模型。 GWAE 提供了一個基於變分自編碼器(VAE)模型架構的表示學習新框架。與傳統基於 VAE 的表示學習方法針對資料變數的生成建模不同,GWAE 透過資料和潛在變數之間的最優傳輸獲得有益的表示。 Gromov-Wasserstein(GW)度量使得在不可比較變數之間(例如具有不同維度的變數)進行這種最優傳輸成為可能,其側重於所考慮的變數的距離結構。透過以 GW 度量取代 ELBO 目標,GWAE 在資料和潛在空間之間執行比較,直接針對變分自編碼器中的表示學習(如圖 1)。這種表示學習的表述允許學習到的表示具有特定的被認為有益的屬性(例如分解性),這些屬性被稱為元先驗。
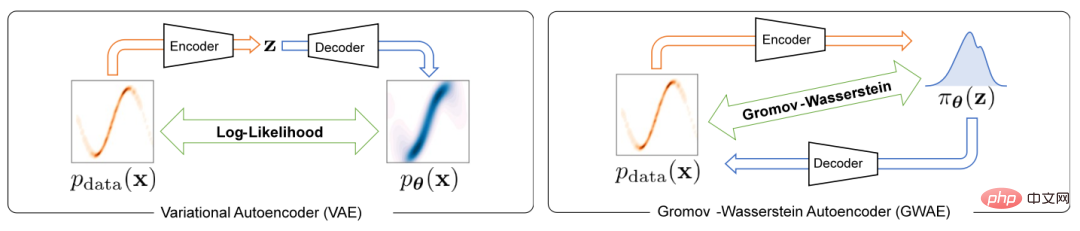
圖1 VAE 與GWAE 的差異
##本研究目前已被ICLR 2023 接受。
- 論文連結:https://arxiv.org/abs/2209.07007
- #程式碼連結:https://github.com/ganmodokix/gwae
資料分佈與潛在先驗分佈之間的GW目標定義如下:
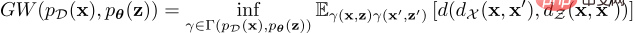
這種最優傳輸代價的公式可以衡量不可比空間中分佈的不一致性;然而對於連續分佈,由於需要對所有耦合進行下確界,計算精確的GW 值是不切實際的。為了解決這個問題,GWAE 解決了一個鬆弛的最佳化問題,以此來估計和最小化 GW 估計量,其梯度可以透過自動微分進行計算。鬆弛目標是估計的 GW 度量和三個正則化損失的總和,可以在可微編程框架(如 PyTorch)中全部實現。此鬆弛目標由一個主要損失和三個正則化損失組成,即主要估計的 GW 損失,基於 WAE 的重構損失,合併的充分條件損失以及熵正則化損失。
這個方案還可以靈活地自訂先驗分佈,以將有益的特徵引入低維表示中。具體而言,該論文引入了三個先驗族群,分別是:
#神經先驗(NP) 在具有NP 的GWAEs 中,使用全連接的神經網路建構先驗採樣器。此先驗分佈族群在潛在變數方面做出了較少的假設,適用於一般情況。
因子化神經先驗(FNP)#在具有FNP 的GWAEs 中,使用本地連接的神經網路建構採樣器,其中每個潛在變數的條目獨立產生。這種採樣器產生一個因子化的先驗和一個逐項獨立的表示,這是代表性元先驗、解糾纏的一種突出方法。
高斯混合先驗(GMP) #在GMP 中,定義為幾個高斯分佈的混合物,其取樣器可以使用重參數化技巧和Gumbel-Max 技巧來實現。 GMP 允許在表示中假設簇,其中先驗的每個高斯組件都預期捕捉一個簇。
實驗及結果
本研究對GWAE 進行了兩個主要元先驗的經驗評估:解糾纏和聚類。
解糾纏 研究使用了 3D Shapes 資料集和 DCI 指標來測量 GWAE 的解糾纏能力。結果表明,使用 FNP 的 GWAE 能夠在單一軸上學習物件色調因素,這表明了 GWAE 的解糾纏能力。定量評估也展示了 GWAE 的解糾纏表現。
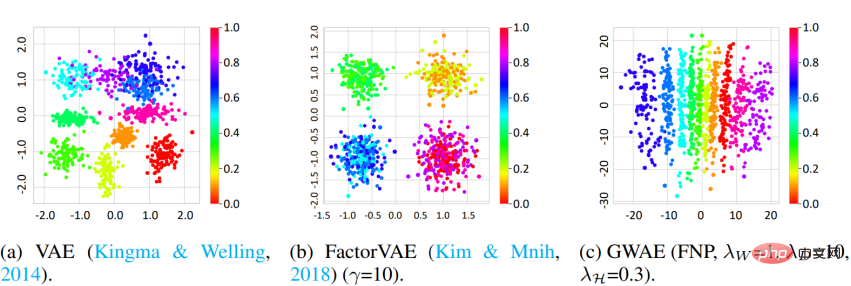
聚類 為了評估基於聚類元先驗獲得的表徵,該研究進行了一項Out-of-Distribution(OoD)偵測。 MNIST 資料集被用作 In-Distribution(ID)數據,Omniglot 資料集被用作 OoD 資料。雖然 MNIST 包含手寫數字,但 Omniglot 包含不同字母的手寫字母。在這個實驗中,ID 和 OoD 資料集共享手寫影像領域,但它們包含不同的字元。模型在 ID 資料上進行訓練,然後使用它們學到的特性來偵測 ID 或 OoD 資料。在 VAE 和 DAGMM 中,用於 OoD 檢測的變數是先驗的對數似然,而在 GWAE 中,它是 Kantorovich potential。 GWAE 的先驗是用 GMP 建構的,以捕捉 MNIST 的簇。 ROC 曲線顯示了模型的 OoD 檢測性能,其中所有三個模型都實現了近乎完美的性能;然而,使用 GMP 構建的 GWAE 在曲線下面積(AUC)方面表現最佳。
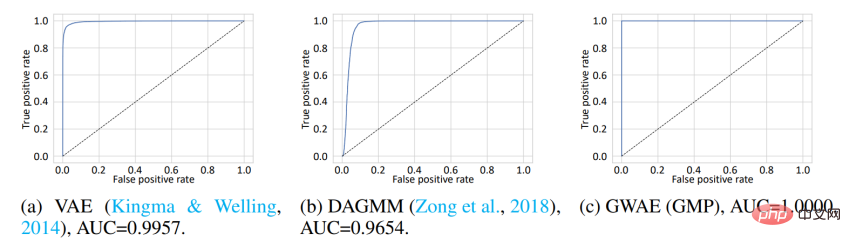
此外研究對 GWAE 進行了生成能力的評估。
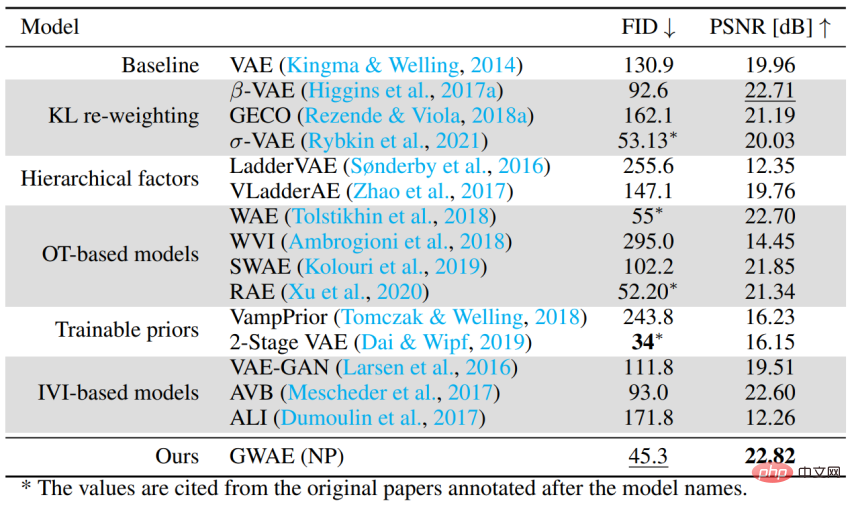
作為基於自動編碼器的生成模型的性能 為了評估GWAE 在沒有特定元先驗的情況下對一般情況的處理能力,使用CelebA 數據集進行了生成性能的評估。實驗使用 FID 評估模型的生成性能,使用 PSNR 評估自編碼性能。 GWAE 使用 NP 獲得了第二好的生成性能和最佳的自編碼性能,這表明其能夠在其模型中捕捉資料分佈並在其表示中捕捉資料資訊的能力。
總結
- #GWAE 是基於Gromov-Wasserstein 度量所建構的變分自編碼器產生模型,旨在直接進行表示學習。
- 由於先驗只需要可微分樣本,因此可以建立各種先驗分佈設定來假設元先驗(表示的理想特性)。
- 在主要元先驗上的實驗以及作為變分自編碼器的性能評估表明了 GWAE 公式的靈活性和 GWAE 的表示學習能力。
- 第一作者Nao Nakagawa 個人首頁:https://ganmodokix.com/note/cv
- 日本北海道大學多媒體實驗室首頁:https://www-lmd.ist.hokudai.ac.jp/
以上是解決VAE表示學習問題,北海道大學提出新型生成模式GWAE的詳細內容。更多資訊請關注PHP中文網其他相關文章!

