詳解二元樹的遍歷以及進行邏輯操作的方法
- 醉折花枝作酒筹轉載
- 2021-07-26 17:43:341703瀏覽
首先,我們還是要說明一下,我們學習的主要內容是二元樹,因為二元樹是最典型的一種樹的應用,不管是考試還是面試,它都是必知必學的內容。

首先,在學習樹的操作之前,我們先明白在樹的操作中,最核心的就是「遍歷」。為什麼這麼說呢?有別於棧和佇列,樹結構其實已經不是一維的了,它有分支,有不同的角度,更重要的是它有了層級的概念。
一維空間的東西就是我們常見的“線”,它只有長度,沒有高度,而這個長度就是它唯一的維度,堆疊和佇列很明顯都是一維的。而樹就不同了,因為層級的概念,所以它有了“高度”,也就是說,它升級到了二維的概念。就像上一篇文章介紹的那一堆名詞中,就有「樹的高度(深度)」的概念。
能夠遍歷一顆樹之後,我們就可以在遍歷的基礎上對這顆樹的結點進行增、刪、改等操作,這些基本的邏輯操作全都是建立在遍歷的基礎之上的,仔細回想一下棧和佇列,其實它們的這些邏輯操作不也是從遍歷入手嗎?不管是出棧入棧還是出隊入隊,我們都是建立在固定的遍歷規則之下的(FILO、FIFO)。
對於二維的事物,如何遍歷它就是一個重點的內容。一維的資料結構我們只要順序地去遍歷就可以了,而二維的資料結果則不能簡單的按順序一個一個地去遍歷了,因為結點之間有層次關係的存在,所以我們要考慮當前的結點如果沒有子結點了,我們的遍歷作業該怎麼辦呢?
幸好,我們是站在巨人的肩膀上來學習這些知識。許多的前輩已經為我們總結了一些非常簡單的對於樹的遍歷方法,有多簡單呢?先賣個關子,我們先來看看如何建立一顆樹,也就是我們在上篇文章中展示過的二元樹。
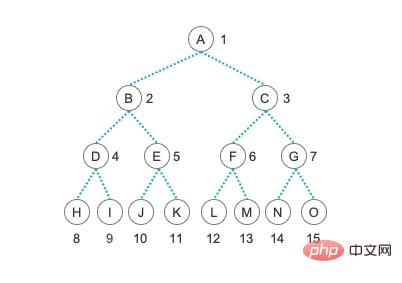
二元樹的鍊式儲存結構
使用鍊式儲存二元樹非常簡單,而且也很形象,小夥伴們先收起對順序儲存二元樹的疑問,因為在下一篇文章中我們就會講解在什麼情況下使用順序儲存。
class BiTree
{
public $data;
public $lChild;
public $rChild;
}其實,在鍊式儲存中,我們就是使用一個個結點來保存這顆樹。每個二元樹結點都有一個資料域,也就是 data 屬性。另外兩個屬性就可以看做是兩個分叉的指針,分別是這個結點的左孩子結點 lChild 和右孩子結點 rChild 。
對比堆疊和佇列來說,我們只是將 next 結點換成了左、右兩個孩子結點而已,本質上其實與堆疊和佇列並沒有太大的差別。說穿了,從資料結構來看,我們還是用一維的儲存來表示二維的概念,而這個概念的轉變則是我們需要從對概念理解的角度出發的。
二元樹建樹
// 建立二叉树
function CreateBiTree($arr, $i)
{
if (!isset($arr[$i])) {
return null;
}
$t = new BiTree();
$t->data = $arr[$i];
$t->lChild = CreateBiTree($arr, $i * 2);
$t->rChild = CreateBiTree($arr, $i * 2 + 1);
return $t;
}就這麼簡單的方法,我們就可以完成一個鍊式二元樹的建立。小夥伴們請仔細看好了,這一個簡單的建樹操作其實內含不少玄機:
#我們使用一個數組來依次表示樹的各個結點,比如依次輸入A 、 B 、 C 、 D 、 E …… (樹的順序存儲中我們會再次看到它們的身影)
賦值的內容是當前$i 下標的數據,注意我們在給左、右孩子賦值時進行了遞歸操作
在學習堆疊的時候,我們學習過「遞歸」就是一種堆疊式的操作,所以,在這段程式碼中,我們是以堆疊的形式來建造樹的
注意到每次的i 2 和i 2 1 了吧?請複習二元樹的 性質5
最後我們測試這個方法是否能夠成功的建立一顆鍊式樹結構。
$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O']; $tree = CreateBiTree($treeList, 1); print_r($tree); // BiTree Object // ( // [data] => A // [lChild] => BiTree Object // ( // [data] => B // [lChild] => BiTree Object // ( // [data] => D // [lChild] => BiTree Object // ( // [data] => H // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => I // [lChild] => // [rChild] => // ) // ) // [rChild] => BiTree Object // ( // [data] => E // [lChild] => BiTree Object // ( // [data] => J // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => K // [lChild] => // [rChild] => // ) // ) // ) // [rChild] => BiTree Object // ( // [data] => C // [lChild] => BiTree Object // ( // [data] => F // [lChild] => BiTree Object // ( // [data] => L // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => M // [lChild] => // [rChild] => // ) // ) // [rChild] => BiTree Object // ( // [data] => G // [lChild] => BiTree Object // ( // [data] => N // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => O // [lChild] => // [rChild] => // ) // ) // ) // )
列印出來的內容應該非常清晰了吧? A 結點有左右兩個孩子結點分別是 B 和 C ,B 結點有左右兩個孩子分別是 D 和 E ,依序類推。最終的結構和我們上面那個二元樹圖的結構完全一致。在這裡,我們還需要注意的一點是,對於傳遞進來的數組,我們給第一個元素,也就是 0 下標的資料為空,並且是從第二個元素也就是 1 下標的元素開始建樹的。這樣也是為了能夠直覺方便的利用二元樹的 性質5 來快速地建立這顆樹。
二叉树的遍历
说完二叉树的建树了,其实我们就已经接触到了一种二叉树的遍历形式。注意看我们建树方法中的代码,我们是先给结点的 data 赋值,然后建立这个结点的左、右孩子结点,并为它们赋值后再继续使用同样的操作一路建立完成所有的结点。现在,我们将这个操作反过来,不是建立结点,而是读取这些结点的内容,先读取结点的内容,然后再读取这个结点左右孩子结点的内容,这就是“先序遍历”。
先序遍历
/**
* 前序遍历
*/
function PreOrderTraverse(?BiTree $t)
{
if ($t) {
echo $t->data, ',';
PreOrderTraverse($t->lChild);
PreOrderTraverse($t->rChild);
}
}
PreOrderTraverse($tree);
// A,B,D,H,I,E,J,K,C,F,L,M,G,N,O,是不是很神奇?就连建树我们竟然也使用的是同一种遍历的方法,可以看出对于二叉树这种复杂的数据结构来说,遍历的重要作用了吧。
大家可以看一个遍历读取出来的结点顺序,貌似和我们输入的顺序不一样呀!没错,先序遍历是通过递归,先按一个方向走到底,当这个结点没有子结点之后,通过递归栈的特性再向上弹出。并且在遍历孩子结点之前先输出当前这个结点的内容。注意,这一句话很重要!所以我们的顺序就是 A,B,D,H ,当 H 没有子结点之后,我们就回到父结点 D 再进入它的右子结点 I ,具体顺序可以参考下图:
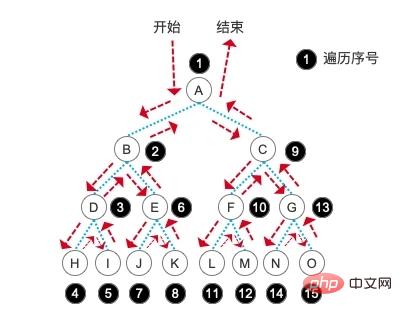
我们代码中的先序遍历和先序建树的结点顺序是完全不一样的,这一点也是要搞清楚的。建树的过程我们根据二叉树的 性质5 直接为它指定了数据下标。而在遍历过程中则是一个结点一个结点的去扫描遍历整颗树的。
中序遍历
顾名思义,中序遍历其实就是在遍历完左孩子结点之后再输出当前这个结点的内容,所以我们只需要微调先序遍历的代码即可。
/**
* 中序遍历
*/
function InOrderTraverse(?BiTree $t)
{
if ($t) {
InOrderTraverse($t->lChild);
echo $t->data, ',';
InOrderTraverse($t->rChild);
}
}
InOrderTraverse($tree);
// H,D,I,B,J,E,K,A,L,F,M,C,N,G,O,中序遍历的步骤就是我们会直接先走到最左边的子结点,当遇到最后一个结点时,输出内容,也就是图中的 H 结点,接着回到它的父结点 D 结点,这时根据中序的原理输出 D ,再进入它的右孩子结点并输出 I 。
D 结点的子树及它本身遍历完成后,返回 D 结点的上级结点 B 结点,输出 B ,然后进入 B 结点的右孩子结点 E 。再次进入到 E 的最左孩子结点 J ,然后参考 D 结点的遍历形式完成整颗树的遍历。具体顺序参考下图:
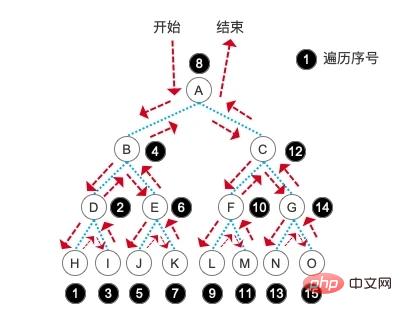
后序遍历
在学习了先序和中序之后,从名字就可以看出来后序就是在遍历完一个结点的左右孩子之后最后输出这个结点的内容,代码当然也是简单地微调一下就可以了。
/**
* 后序遍历
*/
function PostOrderTraverse(?BiTree $t)
{
if ($t) {
PostOrderTraverse($t->lChild);
PostOrderTraverse($t->rChild);
echo $t->data, ',';
}
}
PostOrderTraverse($tree);
// H,I,D,J,K,E,B,L,M,F,N,O,G,C,A,具体原理就不详细说明了,相信在学习了先序和中序之后,你一定能马上想明白后序遍历到底是什么意思了。直接上图:
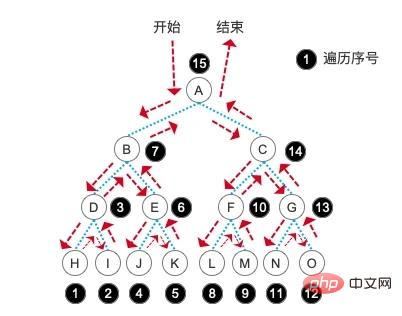
层序遍历
最后,我们要讲的就是层序遍历。既然有“层”这个关键字了,相信大家马上就能联想到,是不是一层一层地去遍历啊!没错,层序遍历就是这个意思,我们按照树的层次,一层一层地输出相应的结点信息。需要注意的,在这里我们会用到队列,而不是栈了。
/**
* 层序遍历
*/
$q = InitLinkQueue();
function LevelOrderTraverse(?BiTree $t)
{
global $q;
if (!$t) {
return;
}
EnLinkQueue($q, $t);
$node = $q;
while ($node) {
$node = DeLinkQueue($q);
if ($node->lChild) {
EnLinkQueue($q, $node->lChild);
}
if ($node->rChild) {
EnLinkQueue($q, $node->rChild);
}
echo $node->data, ',';
}
}
LevelOrderTraverse($tree);
// A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,InitLinkQueue() EnLinkQueue() 、 EnLinkQueue() 这些都是我们之前学习队列的时候所写的对于队列的逻辑操作方法。是不是很开心呀,之前的知识又用上了。层序遍历的核心思想就是运用队列的概念,遇到一个结点,就把这个结点入队,然后判断它是否有子结点,然后相继把子结点入队。
每遍历一个结点,就把队首的结点出队,这样就完成了按树的层次遍历的能力。文字说明还是太抽象,我们还是通过图片来展示这一过程:
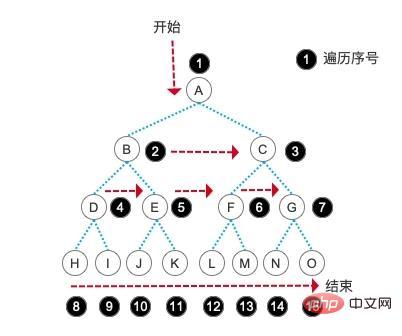
大家有没有发现,层序遍历的输出结果就和我们建树时的数组顺序完全相同了。很好玩吧,所以说代码的世界总是有无穷的乐趣等着我们去发现哦!
总结
今天的内容有没有懵圈?如果懵圈了就多找资料好好研究一下,先序、中序、后序都是利用栈来进行树的结点遍历的,而层序遍历则是利用了队列。一环套一环呀,前面学习的内容都派上用场了吧!不过这只是个开始,在学习图的时候,我们会在深度遍历和广度遍历中再次看到栈和队列的身影,它们可都是亲戚哦。
这四种遍历方式在考试和面试中也是经常出现的,不管是它们的原理还是画图或者是根据图形来写出各种遍历的顺序,都是非常常见的考核内容,所以大家在这篇文章入门的基础上还是要更加深入的去根据一些教材来深入的理解这几种遍历,熟练的掌握它们。
测试代码:
https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/4.树/source/4.2二叉树的遍历及逻辑操作.php
推荐学习:php视频教程
以上是詳解二元樹的遍歷以及進行邏輯操作的方法的詳細內容。更多資訊請關注PHP中文網其他相關文章!

