解析PHP如何實作有趣的漢諾塔演算法

#                                                                                

昨天研究了一天漢諾塔演算法都沒搞懂，並且覺得自己智商被碾壓了，還不如《猩球崛起》中的那一隻猩猩！ ！ ！

起源

傳說最早發明這個問題的人是法國數學家『愛德華·盧卡斯』。

在世界中心貝拿勒斯（在印度北部）的聖廟裡，一塊黃銅板上插著三根寶石針。印度教的主神梵天在創造世界的時候，在其中一根針上從下到上地穿好了由大到小的64片金片，這就是所謂的漢諾塔。不論白天黑夜，總有一個僧侶在按照下面的法則移動這些金片：一次只移動一片，不管在哪根針上，小片必須在大片上面。僧侶們預言，當所有的金片都從梵天穿好的那根針上移到另外一根針上時，世界就將在一聲霹靂中消滅，而梵塔、廟宇和眾生也都將同歸於盡。

這個傳說有很多的變本具體是誰就不得而知了，但是留下的數學問題卻是很經典的。

其留下的數學知識：金片的個數和移動步數的關係為 2^n - 1。

• 1個金片的移動次數2的1次方減1
• 2個金片的移動次數2的2次方減1
• #3個金片的移動次數2的3次方減1
• …
• 個金片的移動次數2的n次方減1

若傳說屬實，僧侶們需要2^64 - 1 步才能完成這個任務；假設他們每秒移動一個金片，就需要5849 億年才能完成。整個宇宙現在也不過137 億年，所以宇宙毀滅還早…（閒的無聊，我還真計算了一下，如下圖）

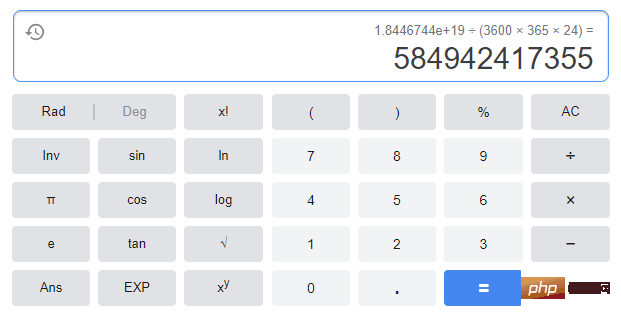
基本規則

漢諾塔演算法有2個基本條件，假設移動的是盤子。

1.每次只能移動一個盤子。
2.小盤子必須要在大盤子的上面。

分析

假設本次遊戲有3根柱子，分別是 A， B， C。其中一根上已經有排序好的盤子N個，最大的在最下面，依序向上盤子越來越小，另外2根空柱。

初始狀態如下圖：

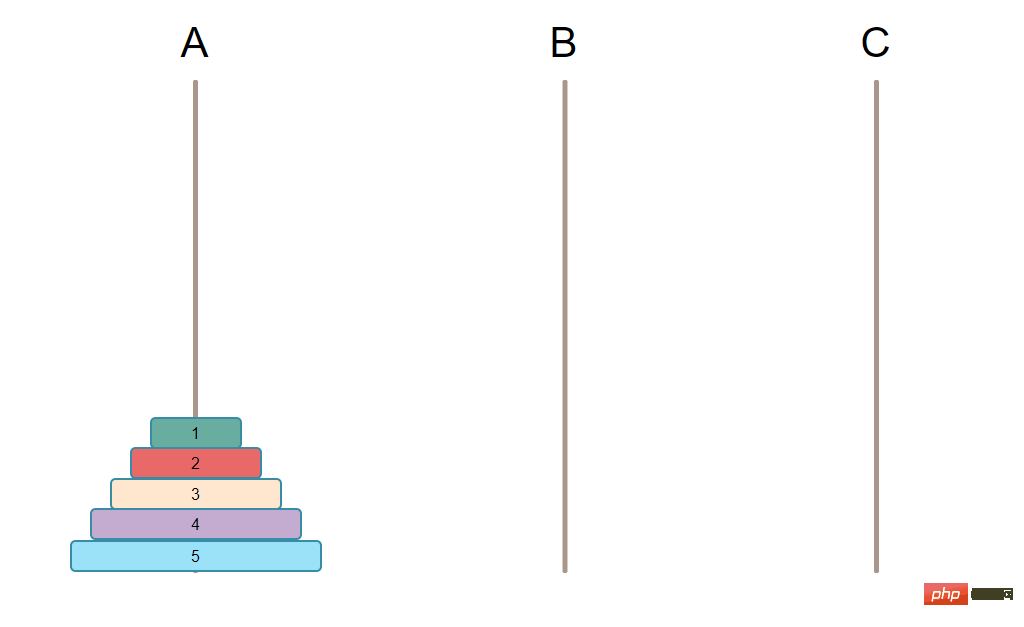
需要實現的最終目標是把柱子上所有的盤子都移到另外一根柱子上。 【推薦學習：PHP影片教學】

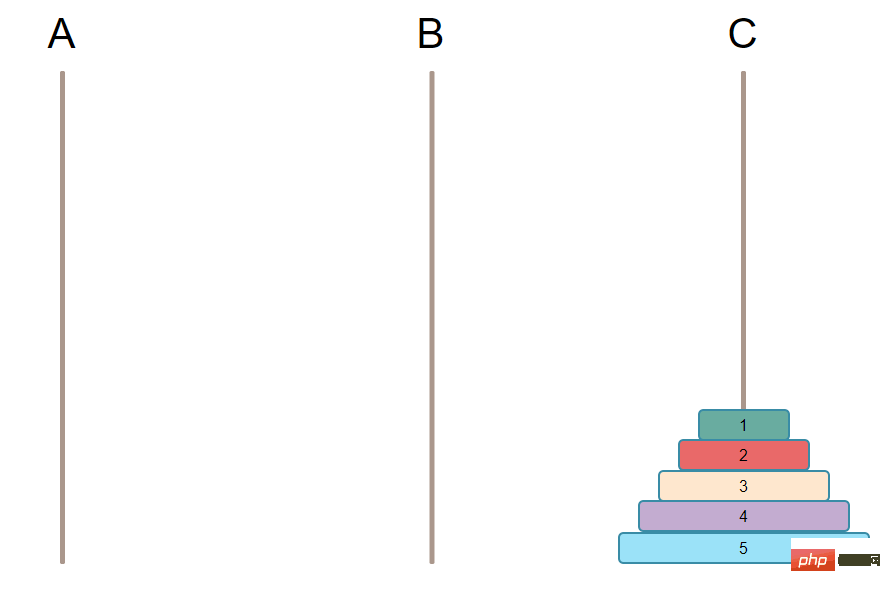
實作的大概想法：

• 拋開腦中想著的每一步要怎麼走，這個很複雜，腦容量估計不夠，先想最簡單粗暴的解決邏輯。
• 要滿足大盤子在下的基本條件，肯定需要先把A上最大的盤子空出來，然後把最大的盤子放到C柱上。假設最大的盤子編號是N。
• 因為要移到C，要實現解析PHP如何實作有趣的漢諾塔演算法，肯定需要把N-1 個盤子都移到B柱子上，只有這樣第N個盤子（也就是最大的盤子）才能移動到C柱子上。
• 把N-1 個盤子移到B柱上，因為要滿足條件大的在下，小的在上，所以這N-1 個盤子在B柱子上也是順序的。
• 最後把這 N-1 個盤子從B柱移到C柱上完成最終目標。

概括下：

解析PHP如何實作有趣的漢諾塔演算法把A上 N-1 個盤子移到B上。

為什麼要先把 N-1 個先移到B上？你看，因為你最後實現的是把A上全部的盤子都移到C上，順序又不能變，只能是大的在下，小的在上。那你一定需要先把最大號的移到C，不然的話就不滿足條件了。

要從A上移動最大號盤子到C上，肯定需要把A上最大號盤子空出來，也就是最大號盤子上面的所有盤子都要搬移走。而你只有3根柱子，C上一定是不能有別的盤子把，不然你就又不滿足條件了，所有這 N-1 個盤子只能放到B上，而且還是有序的。也變成了下圖：

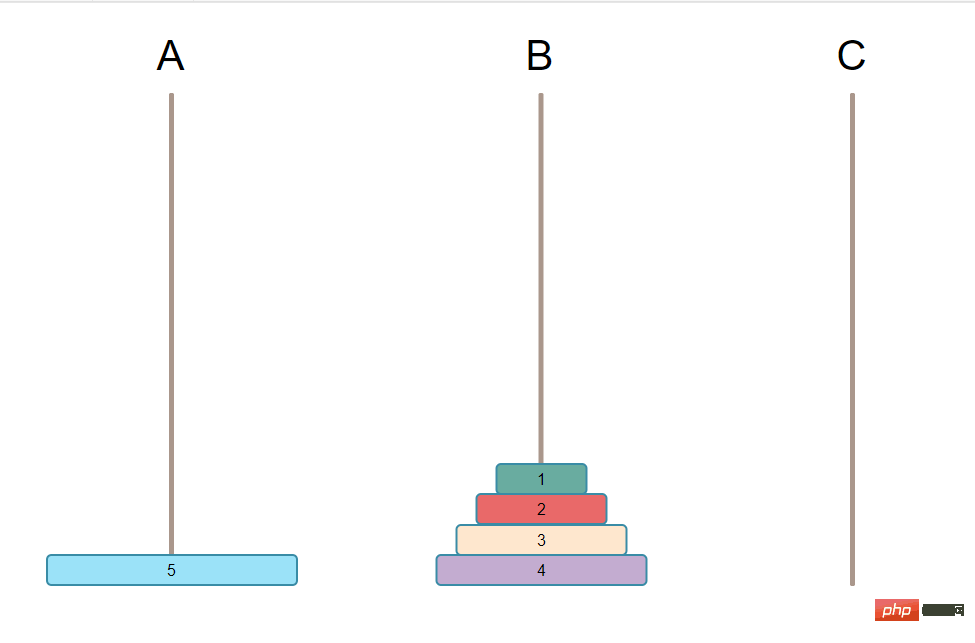
解析PHP如何實作有趣的漢諾塔演算法把A上第 N 個盤子（也就是最大號盤子）移到C上。

這個就很簡單了把，只要一步，把最大號盤子從A移到C就可以了。如下圖：

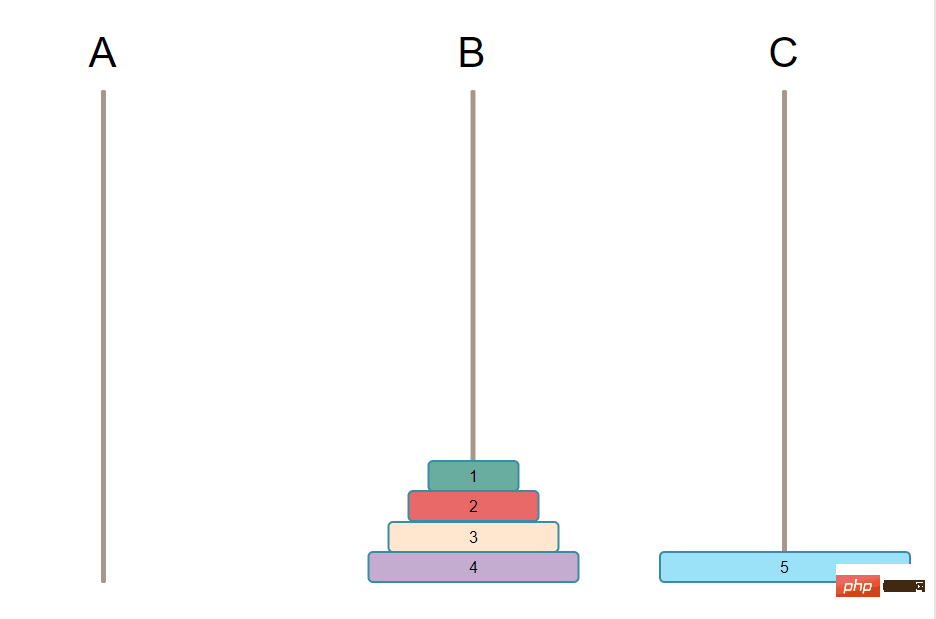
第三步驟把B上 N-1 個盤子移到C上。

注意：要實現把 N-1 個盤子移到C，是不是又變成了找出其中最大盤子，然後先移動最大盤子。所以這裡的話其實變成了重複第 1，2步驟，從這 N-1 個找出最大的先移動到C，循環往復。

那第三步其實等於變更了需求 假設 K = N - 1。
B柱子上有K個盤子，A柱子是空的，C柱子有最大的盤子所以對於K個盤子的B柱子而言等同於空。
解析PHP如何實作有趣的漢諾塔演算法把B上 K-1 個盤子移到A上。
解析PHP如何實作有趣的漢諾塔演算法把B上第 K 個盤子移到C上。
第三步驟把A上 K-1 個盤子移到C上。
…

就變成下圖

先找到剩餘的盤子中最大的

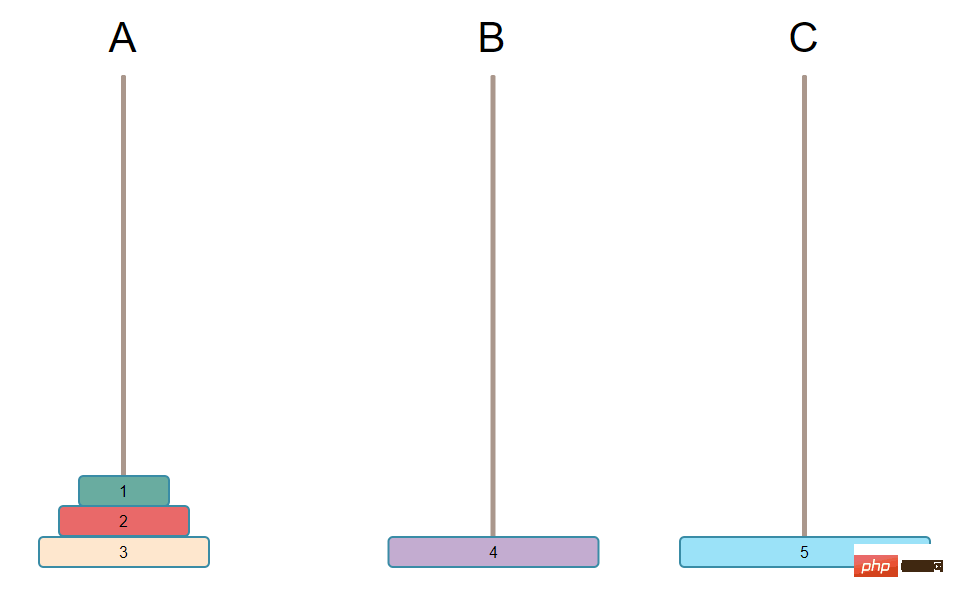
然後再移動最大號盤子

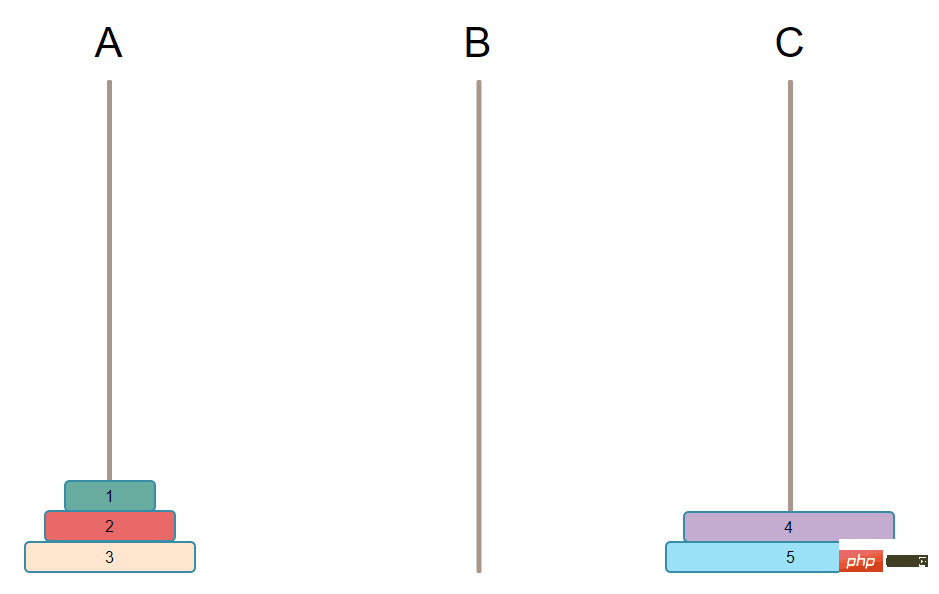
然後循環下去直到只剩下一個盤子，直接移動到C，遊戲結束。

輔助柱

什麼是輔助柱？假設你現在所有待移動的盤子都在A上，目標是移動到C上，那麼B就是 N-1 個盤子的輔助柱子。因為他們只能暫存在這裡，不然就不符合遊戲規則了。

這裡要先找出輔助柱子，不要想怎麼實現，先理清邏輯。

• 要實現從A移動到B，那麼C就是輔助柱
• 要實現從A移動到C，那麼B就是輔助柱
• 要實現從B移動到C，那麼A就是輔助柱

實作

#透過上面的分析可以看到這其實就是一個迴圈往復的重複操作，很類似遞歸，這裡都可以使用遞歸來實現。

要使用遞迴需要有2個必要條件

1.求出遞推公式
2.找到退出條件

退出條件很好寫，肯定是只有一個盤子的時候，直接移動到C柱上。

那麼遞推公式是什麼呢？還是根據上面的邏輯分析，可以分解為3步。

解析PHP如何實作有趣的漢諾塔演算法驟把【N-1個】 盤子先從A移到B
#解析PHP如何實作有趣的漢諾塔演算法驟把【第N個】 盤子從A移到C
第三步驟把【剩下的N-1個】 盤子從B移動到C

#下面是PHP實現的偽代碼：

class HanoiTower
{
    // 计数器
    public $count = 0;
    /**
     * 汉诺塔实现
     * 
     * @param $n 盘子号
     * @param $A 初始柱子
     * @param $B 中转站
     * @param $C 目标柱子
     */
    public function hanoi($n, $A, $B, $C)
    {
        if ($n == 1) {
            // 退出条件 只剩一个盘子的时候直接从A移动到C
            $this->biggestOne($n, $A, $B, $C);
        } else {
            // 解析PHP如何實作有趣的漢諾塔演算法把 【n-1】 个盘子从A移动到B 此时C为中转站
            $this->hanoi($n - 1, $A, $C, $B);
            // 解析PHP如何實作有趣的漢諾塔演算法把 【第n】 个盘子从A移动到C
            $this->biggestOne($n, $A, $B, $C);
            // 第三步把B上 【剩余的n-1个】 盘子从B移动到C 此时A为中转站
            $this->hanoi($n - 1, $B, $A, $C);
        }
    }
    /**
     * 移动最大的盘子
     * 直接从A移动到C
     */
    public function biggestOne($n, $A, $B, $C)
    {
        ++$this->count;
        echo &#39;第&#39;, $this->count, &#39;步 &#39;, &#39;把 &#39;, $n, &#39;从 &#39;, $A, &#39;移动到&#39;, $C, &#39;<br />&#39;;
    }
}
$n = 5;
$hanoiTower = new HanoiTower();
echo &#39;这是一个有 【&#39;, $n, &#39;】 个盘子的汉诺塔：&#39;, &#39;<br />&#39;;
// 调用执行
$hanoiTower->hanoi($n, &#39;A&#39;, &#39;B&#39;, &#39;C&#39;);
echo &#39;总共需要走：【&#39;, $hanoiTower->count, &#39;】 步&#39;;

結果以下是：

                                  之後  

以上是解析PHP如何實作有趣的漢諾塔演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章！