PHP資料結構-圖的遍歷:深度優先與廣度優先
- 藏色散人轉載
- 2021-07-01 13:42:082794瀏覽
圖的遍歷:深度優先與廣度優先
在先前的文章《PHP資料結構-圖的儲存結構》中,我們學習完了圖的相關的儲存結構,也就是鄰接矩陣和鄰接表。它們分別就代表了最典型的 順序儲存 和 鍊式儲存 兩種類型。既然資料結構有了,那麼我們接下來當然就是學習這些資料結構的操作啦,也就是演算法的部分。不管是圖還是樹,遍歷都是很重要的部分,今天我們先來學習最基礎的兩種圖的遍歷方式。
樹的遍歷演化到圖的遍歷
還記得在樹的學習中,我們講到過先序、中序、後序以及層序遍歷這幾種遍歷形式嗎?其實先序、中序和後序可以看作是一種遍歷方式,它們都是使用堆疊結構來進行遍歷,特點就是先一條路走到黑,然後再返回來走沒有過的路。而層序遍歷則是使用佇列一層一層地進行遍歷,特點就是先遍歷完子結點,然後再挨個遍歷每個子結點的下一層結點。
複習完了樹的遍歷方式再學習圖的遍歷方式就會非常簡單了,因為在圖的遍歷中,最基礎的也是基於堆疊和佇列的兩種遍歷形式。只不過它們的名字略有不同,基於堆疊的遍歷方式叫作 深度優先遍歷 ,而基於隊列的遍歷方式叫作 廣度優先遍歷 。其實也就是對應著樹中的先、中、後序遍歷和層序遍歷,本質上沒有太大的差別。
【推薦:PHP影片教學】
#深度優先遍歷
我們依然還是從堆疊的遍歷方式入手,也就是圖中的 深度優先遍歷 這種形式。對於棧來說,不斷地將新的結點壓棧,直到發現它沒有其它的子結點後再原路返回,當發現某個結點有其它的結點時再進入子結點壓棧,這就是深度遍歷的思想。
在這裡,需要注意的是我們要記錄一下已經訪問過的結點,當出現多個結點都有連接到某一個結點的路徑時,保證這個結點只訪問過一次。這是和樹結構的最大不同,因為樹是一路向下的,平級結點之間沒有聯繫,一個結點只有一個上級結點。而圖則是任意一個結點都可以和其它任意的結點有關係。
鄰接矩陣
首先,我們來看看鄰接矩陣的深度優先遍歷演算法的實作。現在看不懂沒關係,往下拉去看下圖解,然後結合一起看。當然,更好的方案是自己運作起來。
$visited = []; // 已访问结点
function DFS_AM($graphArr, $x)
{
global $visited;
echo "节点:{$x}", PHP_EOL;
$visited[$x] = true; // 当前结点标记为已访问
// y 就是邻接矩阵中的横行
for ($y = 1; $y <= count($graphArr); $y++) {
// 循环判断第 [x][y] 个数据是否为 1,也就是是否有边
// 并且这个结点没有被访问过
if ($graphArr[$x][$y] != 0 && !$visited[$y]) {
// 进行栈递归,传递的参数是当前这个结点
DFS_AM($graphArr, $y);
}
}
}
BuildGraph($graphArr); // 建立邻接矩阵图
echo '请输入开始遍历的结点(1-结点数):';
fscanf(STDIN, "%d", $startNode); // 输入从第几个结点开始访问
DFS_AM($graphArr, $startNode); // 开始深度优先遍历程式碼量不多吧,使用的就是上篇文章中建立鄰接矩陣的程式碼,如果已經忘了就回去看看或直接從文章最下面的連結去看原始碼吧。
接下來我們進行測試:
# php 5.3图的遍历:深度优先与广度优先.php 输入结点数:4 请输入边数:3 请输入边,格式为 出 入 权:1 2 1 请输入边,格式为 出 入 权:1 3 1 请输入边,格式为 出 入 权:3 4 1 请输入开始遍历的结点(1-结点数):3 节点:3 节点:1 节点:2 节点:4
鄰接表
當然,鄰接表的遍歷思想也是相同的,只是中間的循環演算法使用的是鍊式特點的方式。
$visited = []; // 已访问结点
function DFS_AL($graph, $x){
global $visited;
$p = $graph->adjList[$x]; // 指定结点的第一个边结点
echo "节点:{$x}", PHP_EOL; // 输出指定结点的信息
$visited[$x] = true; // 设置该结点已被访问
while($p != null){
$y = $p->adjVex; // 获得边结点信息
if(!$visited[$y]){ // 如果结点没有被访问过
DFS_AL($graph, $y); // 进入这个边结点的深度遍历过程
}
$p = $p->nextArc; // 移动到下一个边结点
}
}
$graph = BuildLinkGraph();
$graphBFS = $graph;
echo '请输入开始遍历的结点(1-结点数):';
fscanf(STDIN, "%d", $startNode); // 输入从第几个结点开始访问
DFS_AL($graph, $startNode);// 开始深度优先遍历是不是也很簡單,接下來也是簡單地測試一下:
# php 5.3图的遍历:深度优先与广度优先.php 请输入 结点数 边数: 4 3 请输入边,格式为 出 入 权:1 2 1 请输入边,格式为 出 入 权:1 3 1 请输入边,格式为 出 入 权:3 4 1 请输入开始遍历的结点(1-结点数):3 节点:3 节点:4 节点:1 节点:2
輸出的順序怎麼跟鄰接矩陣的不太一樣?我們在上篇文章中實現的鄰接表使用的是頭插法,後輸入的數據添加在結點鏈接的前面,如果我們將3 4 1 放在第一個輸入的話,那麼結點就和鄰接矩陣的遍歷結果一樣了。
深度優先遍歷圖示
#直接就上來看了程式碼,又講了半天演算法,是不是還是一頭霧水?沒關係,我們直接上圖看看:
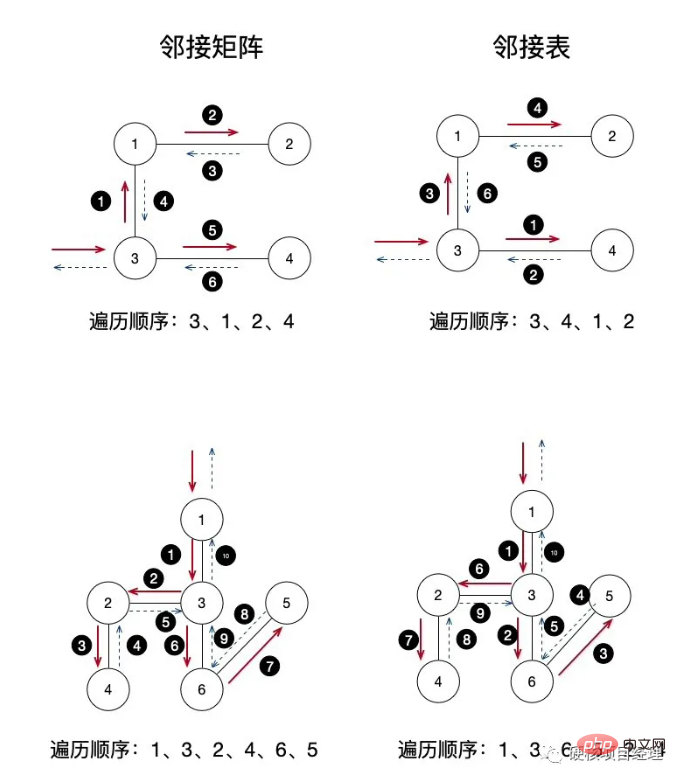
左邊是鄰接矩陣的,右邊是鄰接表的。我們測試的圖比較簡單,4 個結點 3 條邊,下面是複雜一些有 6 個結點 5 條邊的圖。大家可以自己測試一下。每一步的遍歷和執行順序看小黑圓的數字。下面我們以鄰接矩陣的第一張圖來簡單地講解下訪問的步驟:
#首先我們輸入從結點3 開始訪問,然後開始深度遍歷,這時輸出結點3
第一步結點3 的循環中獲得它和結點1 有邊,於是遞歸傳入結點1 ,結點1 入棧
輸出結點1,目前的遞迴中結點1 在堆疊頂部
在 结点1 的循环中发现 结点1 和 结点 2 有边,于是递归传入 结点2 ,结点2 入栈
输出 结点2,目前的递归中 结点2 在栈顶
注意了,重点在这里,结点2 的循环中没有发现与其它未访问的结点有边存在了,于是递归开始返回,也就是开始出栈了,依次返回到 结点1 、结点3,没有任何输出,栈空了,递归回到最外层的函数了
继续 结点3 的循环,发现与 结点4 有边,递归传入 结点4
输出 结点4,目前的递归中 结点4 在栈顶
结点4 的循环中没有发现其它未访问的结点及边了,递归返回,结点4 出栈
结点3 循环完成,遍历结束
一步一步的很清晰吧,大家试着自己分析一下下面那个复杂一些图的深度遍历顺序,看看和我们程序输出的结果是不是一样的。在很多的考研或者数据结构考试中,经常会有选择题或应用题让你手动地来写出深度优先遍历的顺序哦!
广度优先遍历
接下来就是广度优先遍历了,其实说白了就是我们在学习树的遍历时候的层序遍历。前面我们说过,深度遍历是一条路走到黑,没路了退回来。而广度遍历则是一层一层的查看,直到找到出口。
邻接矩阵
使用邻接矩阵来进行广度优先遍历的操作,其实最核心的遍历方式和深度遍历没什么区别,都是对某一个结点进行边的查找,唯一不同的就是把递归栈换成了队列而已。
$visited = [];
function BFS_AM($graphArr, $x){
global $visited;
$queue = InitSqQueue(); // 初始化队列
$graphCount = count($graphArr); // 获取矩阵结点数量
$visited[$x] = true; // 结点标记为已访问
EnSqQueue($queue, $x); // 结点入队
while($x){ // 循环判断结点是否 fasle
// 遍历所有结点是否与这个结点有边
for ($y = 1; $y <= $graphCount; $y++) {
// 如果有边并且未访问过
if ($graphArr[$x][$y] != 0 && !$visited[$y]) {
$visited[$y] = true; // 结点标记为已访问
EnSqQueue($queue, $y); // 结点入队
}
}
$x = DeSqQueue($queue); // 出队一个结点
echo $x, PHP_EOL; // 输出结点
}
}
echo '请输入开始广度遍历的结点(1-结点数):';
fscanf(STDIN, "%d", $startNode);
BFS_AM($graphArr, $startNode); // 开始广度遍历代码中的注释也很清晰明了了,我们直接进行测试:
…… …… 请输入开始广度遍历的结点(1-结点数):3 3 1 4 2
邻接表
同样地,我们也提供邻接表的链式广度优先遍历的核心函数。
$visited = [];
function BFS_AL($graph, $x){
global $visited;
$visited[$x] = true; // 结点标记为已访问
$queue = InitSqQueue();// 初始化队列
EnSqQueue($queue, $x); // 结点入队
// 如果一直有能出队的结点,就一直循环
// 也就是说,如果队列空了,循环就结束
while(($i = DeSqQueue($queue))!==false){
echo $i, PHP_EOL; // 输出结点
$p = $graph->adjList[$i]; // 结点的第一个边结点
while($p != null){ // 如果不为空
$y = $p->adjVex; // 边结点信息
if(!$visited[$y]){ // 如果没有访问过
$visited[$y] = true; // 标记结点为已访问
EnSqQueue($queue, $y); // 入队结点
}
$p = $p->nextArc; // 结点指针指向下一个
}
}
}
echo '请输入开始遍历的结点(1-结点数):';
fscanf(STDIN, "%d", $startNode);
BFS_AL($graph, $startNode); // 开始广度遍历核心的循环中的操作其实也和深度遍历没什么太大的区别,同样是换成了队列这种存储形式而已。
…… …… 请输入开始广度遍历的结点(1-结点数):3 3 4 1 2
广度优先遍历图示
好吧,上面又罗列完了算法,接下来就是图示的时间了,相信还是一看图大家就马上能明白广度优先遍历的具体步骤了。
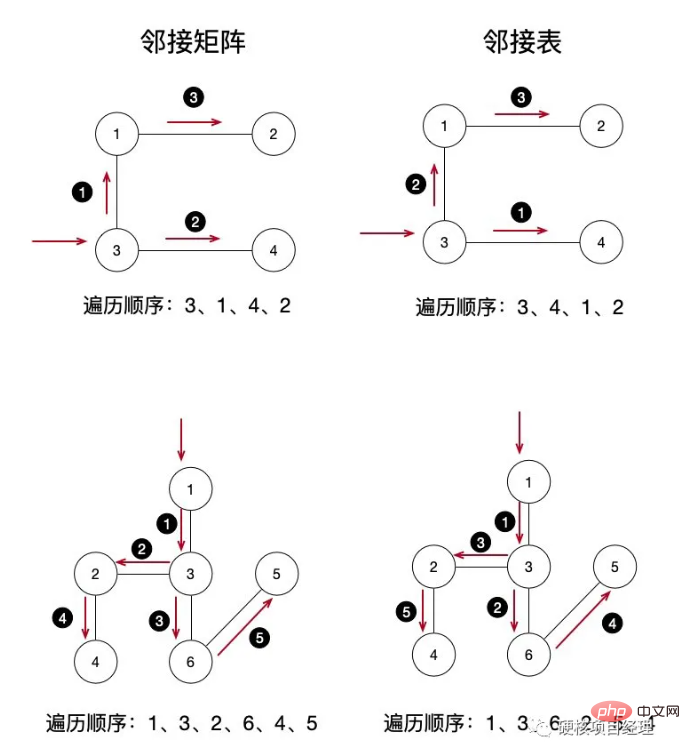
和上面的图一样,同样还是左边是邻接矩阵,右边是邻接表。在这里,我们依然还是直接分步骤来看一下左边最上面图的遍历操作顺序:
输入 结点3 开始广度遍历,结点标记为已访问,这时 结点3 入队
使用 while 循环判断 结点x 是否为 null ,如果不为 null 进入循环体
遍历所有结点是否与这个结点有边,如果有边,并且这个结点没有被访问过,标记已访问,加入队列
出队一个元素,并赋值给 x
输出 x 结点的信息
广度优先遍历没有栈的回溯,就是一条线性的队列走完就完了,所以图示会非常清晰。单独一个结点我们会将和它相关的所有结点入队,然后出队最顶上的结点,这样就能够像树的层序遍历一样按照一层一层的顺序来遍历整个图。同样地,拿起纸笔,找复杂一点的图,试试能不能手写出类似于广度优先遍历顺序的题目吧!
总结
大家学完了之后是不是发现今天介绍的深度优先和广度优先两种遍历方式真的和树的遍历方式没什么太大的区别。最大的不同就是我们要标记已访问过的结点而已。不管怎么说,使用栈和队列来对树或图进行遍历是所有树和图的操作算法中最最基础的部分,也是考试和面试中最常见的问题,大家一定要深入理解掌握哦!
测试代码: https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.3图的遍历:深度优先与广度优先.php
以上是PHP資料結構-圖的遍歷:深度優先與廣度優先的詳細內容。更多資訊請關注PHP中文網其他相關文章!

