中序遍歷是怎麼遍歷的

中序遍歷的遍歷方法為：對於目前結點，首先遍歷左子樹，然後存取目前節點，最後遍歷右子樹。中序遍歷是二元樹遍歷的一種，也叫做中根遍歷、中序週遊。

本教學操作環境：windows7系統、C 17版本、Dell G3電腦。

二元樹是一種重要的資料結構，對二元樹的遍歷也很重要。這裡簡單介紹三種二元樹中序遍歷的方法。二元樹的中序遍歷就是先遍歷左子樹，然後訪問目前節點，最後遍歷右子樹。對於下面的二元樹，中序遍歷結果如下：

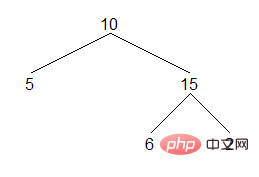
#結果：[5,10,6,15,2]

直觀來看，二元樹的中序遍歷就是將節點投影到一條水平的座標上。如圖：

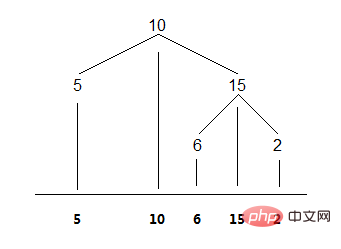
1、遞歸法

#這是思路最簡單的方法，容易想到並且容易實現。遞歸的終止條件是目前節點是否為空。首先遞歸呼叫遍歷左子樹，然後存取目前節點，最後遞迴呼叫右子樹。程式碼如下：

//recursive
class Solution1 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        inorderHelper(ret,root);
        return ret;
    }
private:
    void inorderHelper(vector<int>& ret,TreeNode* root)
    {
        if(root==NULL)return;
        inorderHelper(ret,root->left);
        ret.push_back(root->val);
        inorderHelper(ret,root->right);
    }
};

2、迭代法

在迭代方法中，從根節點開始找二元樹的最左節點，將走過的節點保存在一個堆疊中，找到最左節點後訪問，對於每個節點來說，它都是以自己為根的子樹的根節點，訪問完之後就可以轉到右兒子上了。程式碼如下：

//iterate,using a stack
class Solution2 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        TreeNode *curr=root;
        stack<TreeNode*> st;
        while(!st.empty()||curr!=NULL)
        {
            while(curr!=NULL)
            {
                st.push(curr);
                curr=curr->left;
            }
            curr=st.top();
            st.pop();
            ret.push_back(curr->val);
            curr=curr->right;
        }
        return ret;
    }
};

這個方法時間複雜度是O(n)，空間複雜度也是O(n)。

3、Morris法

這種方法是Morris發明的，看完之後感覺精妙無比。這種方法不使用遞歸，也不使用棧，O(1)的空間複雜度完成二元樹的遍歷。這個方法的基本想法就是將所有右兒子為NULL的節點的右兒子指向後繼節點（對於右兒子不為空的節點，右兒子就是接下來要造訪的節點）。這樣，對於任意一個節點，當訪問完它後，它的右兒子已經指向了下一個該訪問的節點。對於最右節點，不需要進行這樣的操作。請注意，這樣的操作是在遍歷的時候完成的，完成存取節點後會把樹還原。整個循環的判斷條件為目前節點是否為空。例如上面的二元樹，遍歷過程如下（根據當前節點c的位置）：

（1）當前節點為10，因為左兒子非空，不能訪問，找到c的左子樹的最右節點p：

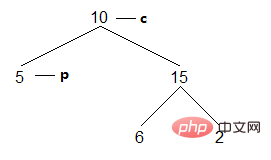
結果：[]

（2）找節點c的左子樹最右邊的節點有兩種終止條件，一種右兒子為空，一種右兒子指向目前節點。下面是右兒子為空的情況，這種情況先要構造，將節點p的右兒子指向後繼節點c，然後c下移：

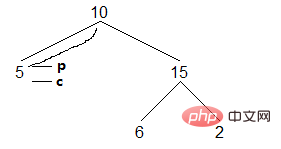
結果：[]

（3）目前節點c的左兒子為空，進行存取。訪問後將c指向右兒子（即後繼節點）：

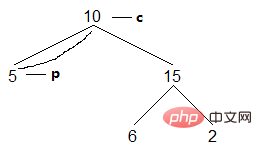
結果：[5]

（4）繼續尋找左子樹的最右節點，這次的終止條件是最右邊節點為目前節點。這說明目前節點的左子樹遍歷完畢，存取目前節點後，還原二元樹，將目前節點指向後繼節點：

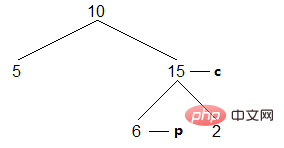
結果：[5,10 ]

（5）重複上述過程，直到c指向整棵二元樹的最右節點：

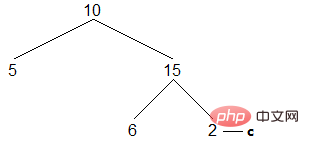
左兒子為空，進行訪問，c轉到右兒子。右兒子為空，不滿足判斷條件，循環結束，遍歷完成。結果如下：

[5,10,6,15,2]

這就是Morris方法，時間複雜度為O(n)，空間複雜度是O(1)。程式碼如下：

//Morris traversal,without a stack
class Solution3 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        TreeNode *curr=root;
        TreeNode *pre;
        while(curr)
        {
            if(curr->left==NULL)
            {
                ret.push_back(curr->val);
                curr=curr->right;
            }
            else
            {
                pre=curr->left;
                while(pre->right&&pre->right!=curr)
                    pre=pre->right;
                if(pre->right==NULL)
                {
                    pre->right=curr;
                    curr=curr->left;
                }
                else
                {
                    ret.push_back(curr->val);
                    pre->right=NULL;
                    curr=curr->right;
                }
            }
        }
        return ret;
    }
};

推薦教學：《C#》

以上是中序遍歷是怎麼遍歷的的詳細內容。更多資訊請關注PHP中文網其他相關文章！