平衡二元樹和二元排序樹的關係
- 藏色散人原創
- 2020-07-02 09:31:3816425瀏覽
平衡二元樹和二元排序樹並沒有直接的關係,但是二元排序樹的尋找效率與二元樹的形態有關,所有當我們希望二元排序樹的形態是均勻的時候,這樣的二元樹就被稱為平衡二元樹。

1. 二元排序樹
二元排序樹(Binary Sort Tree),又稱二元尋找樹(Binary Search Tree),也稱為二元搜尋樹。
- 二元排序樹定義:
#二元排序樹或是一棵空樹,或是具有下列性質的二元樹:
- 若左子樹不空,則左子樹上所有節點的值均小於它的根節點的值;
- 若右子樹不空,則右子樹上所有節點的值都大於它的根節點的值;
- #左、右子樹也分別為二元排序樹。
如圖下圖所示就是一棵二元排序樹:
對二元排序樹進行中序遍歷,便可得到一個按關鍵字排序的序列,如對上圖進行一次中序遍歷可得到一個有序序列:10,42,45,55,58,63,67,70,83,90,98
- #二元排序樹的查找分析
就查找的平均時間效能而言,二元排序樹上的查找與折半查找類似,但就維護表的有序性而言,二元排序樹更有效率,因為它無需移動節點,只需修改指標即可完成二元排序樹的插入和刪除操作。
二元排序樹查找在最壞的情況下,需要的查找時間取決於樹的深度:
- 當二元排序樹接近滿二叉樹時,其深度為 n# ,因此最壞情況下的尋找時間為O(log_2n##g
-

#2
-
平衡二元樹定義
平衡二元樹(Balanced Binary Tree),它是一棵空樹,或是具有以下性質:
- 它的左右兩個子樹的深度差的絕對值不超過1;
- 它的左右兩個子樹也分別是平衡二元樹。
將二元樹節點的左子樹的深度減去它的右子樹的深度稱為平衡因子BF,則平衡二元樹上所有節點的平衡因子只可能是-1、0和1,如下圖左邊的為平衡二元樹,右邊的為非平衡二元樹。 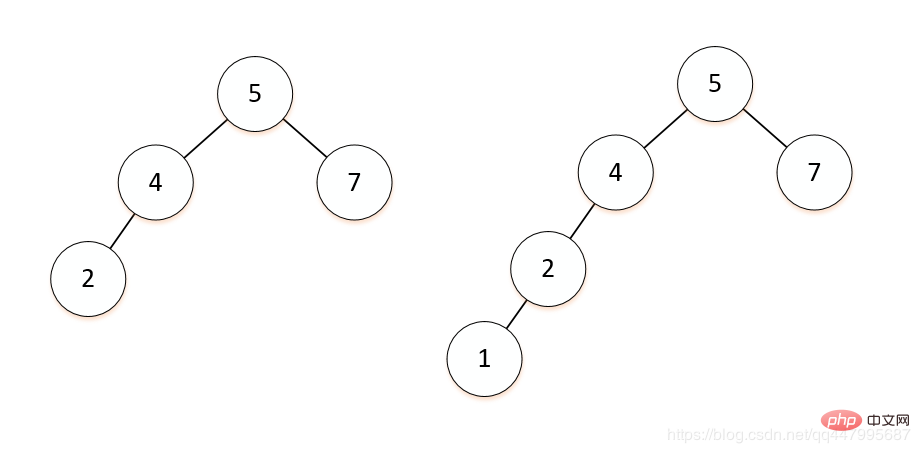
因為平衡二元樹上任何節點的左、右子樹的深度差異都不會超過1,可以證明它的深度和n個節點的完全二元樹的深度#g
#n
####⌋############### 1同數量級的。 ######要建構一棵平衡二元樹,Georgii M. Adelson-Velskii 和Evgenii M. Landis 提出了一種動態保持二元平衡樹的方法,其基本思想是:在建構二元排序樹的時候,每當插入節點時,先檢查是否因插入節點而破壞了樹的平衡性,如果是,則找出其中最小不平衡子樹,在保持排序樹的前提下,調整最小不平衡子樹中各節點之間的連結關係,以達到新的平衡,所以這樣的平衡二元樹簡稱###AVL樹###。其中最小平衡子樹是指:###離插入節點最近,且平衡因子絕對值大於1的節點作為根節點的子樹###。 ###- 調整最小不平衡子樹一般有四種情況:
- #單向右旋(LL型): 插入位置為左子樹的左子樹,以左子樹為軸心,進行單次向右旋轉,如下圖所示。節點旁邊的數字為該節點的平衡因子,I節點為當前插入節點(如果I節點處於正中,則表示I節點既可以是左孩子也可以是右孩子。
注意LL型,以中間節點為軸心旋轉。為什麼這裡I為BL左孩子不能將B-BL-I作為LL型,是因為A節點才是離I節點最近的平衡因子絕對值>1的子樹,其餘節點的平衡因子絕對值都沒有超過1;同理當I為BL右孩子,也不能將B-BL-I作為LR型 。
2. 單向左旋(RR型): 插入位置為右子樹的右子樹,右子樹為軸心,進行單次向左旋轉
注意RR型,以中間節點為軸心進行旋轉。這裡I為左右子樹並不影響其實RR型,原理同上。
# 3. 雙向旋轉先左後右(LR型):插入位置為左子樹的右子樹,要進行兩次旋轉,先向左旋轉,再向右旋轉。
#插入節點為左孩子:注意為什麼不能B-C-I作為子樹將其定為RL型,原理同RR型中的解釋,對於LR型,,是以R端或L靠近插入節點端作為旋轉軸心(如下圖相當於先旋轉以B為根的子樹後,成為了LL型,再旋轉以A為根的子樹)。
插入節點為右孩子:
4. 雙向旋轉先右後左(RL型):插入位置為右子樹的左子樹,進行兩次調整,先右旋轉再左旋轉;處理情況與LR類似。
插入節點為左孩子: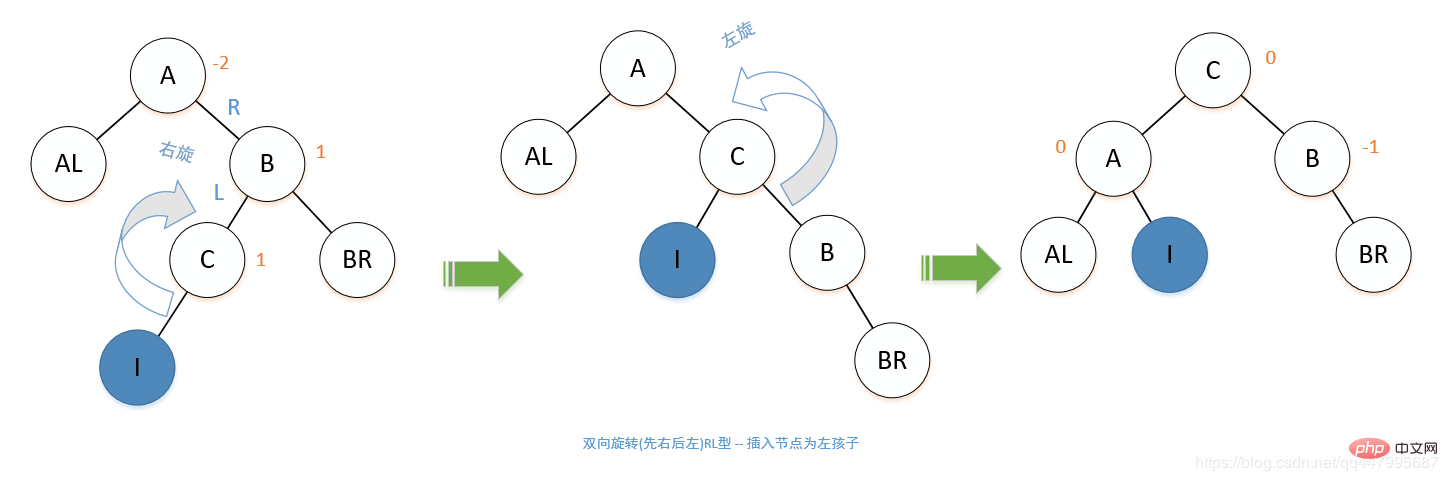
插入節點為右孩子:
經過上面的我們可以發現,平衡因子與類型有很大的關係,需要以離插入節點最近且平衡因子絕對值>1的節點作為根節點的子樹進行判定是哪種類型。
- 練習
如下圖所示,先插入節點2後,成為LL型,然後整體右旋處理後平衡。
再依序插入8和6之後,節點5的平衡因子絕對值>1,成為RL型,所以先以5為根節點,將其子樹8-6右旋(成為RR型),然後將5為根節點的整棵樹再左旋。
繼續插入節點9後,節點4的平衡因子>1,成為RR型,所以以4為根節點,將整體左旋。
以上是平衡二元樹和二元排序樹的關係的詳細內容。更多資訊請關注PHP中文網其他相關文章!


