程式設計師，你還能幹幾年？

科技的浪潮奔騰不息，浪潮退去之後，留給我們自己的是方法論？還是過時的技術？

------

我們程式設計師，總喜歡談論所謂“35歲魔咒”，好像“35歲魔咒”成了程式設計師的專利。然而事實上，35歲，是各行各業的職場人都會面臨的問題。

究其根本，35歲是人到中年的轉捩點，如果我們在工作中的價值產出，更多依靠體力，那麼就勢必面臨職業發展開始走下坡路的困境。

程式設計，原本是一種極富創造力，重視抽象思維與邏輯推演的工作，但我們相當一部分人，把程式設計做的像事務性工作，平淡如水，如果這樣，「35歲魔咒」就會困擾我們。

在一個社會群體中，不同的人有不同的選擇，我無意也無法改變大的環境，但希望幫助有意願與「35歲魔咒」鬥爭的程式設計師，找到一點方向，多幹幾年！

從一道面試題說起

楊輝三角是我在面試中經常會問的一個問題，」請編程，按照指定格式輸出前N行的楊輝三角」。

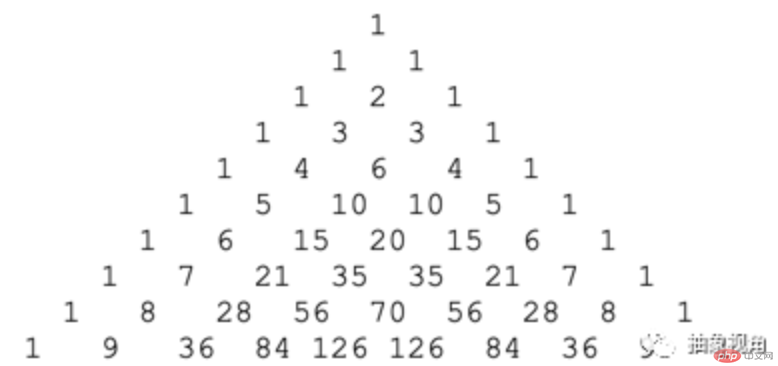
大部分候選人，拿到問題之後，就開始編碼，先寫一個兩層的循環，然後開始思考循環的終止條件，經過一番思考，給出一個自己都不相信的答案。我印像比較深刻的一次，候選人來自微信支付，也僅給出了獲取前N行數據的方法，仍然未能找到按照指定格式打印的方法。

很多人會說，離開學校好幾年了，演算法早都忘了，這種問題應該去問校招的同學。我不以為然，我在意的不是具體的演算法，而是分析解決問題的想法。我們可以忘記一些具體的演算法，但忘記的同時，應該把演算法中蘊含的解決問題的思路內化成自己的武器。

接下來，我跟大家介紹下我如何看待這個問題。

圖靈獎得主N.Wirth提出"程式 = 演算法 資料結構"，我更習慣說「程式 = 資料 流程」。

資料視角

首先，我們站在資料的視角，來檢視這道面試題，可以發現：

1、可以使用二維陣列（以php語言為例）描述楊輝三角形的前N行資料

[
  [1],
  [1, 1],
  [1, 2, 1],
  [1, 3, 3, 1],
]

2、行的資料之間，存在如下規則：

1）每行兩邊數字恆為1

2）每行中間的數字，是上一行交叉位置兩個數字的和

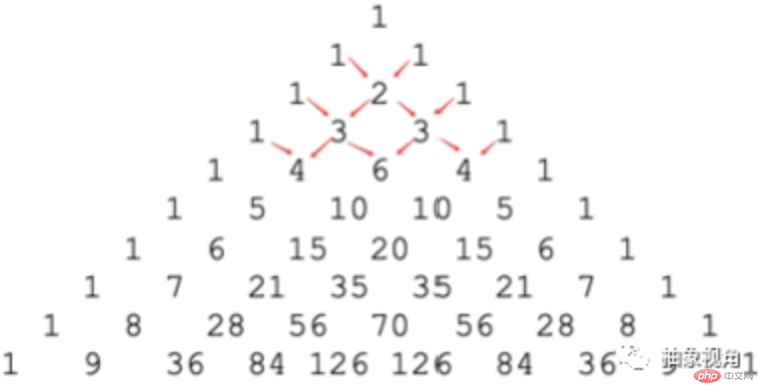
#因此，可以用一個偽代碼描述這種關係：

F(1) = [1]
F(N) = [
    1,
    F(N-1)[0] + F(N-1)[1],
    F(N-1)[1] + F(N-1)[2],
    ...,
    F(N-1)[N-2] + F(N-1)[N - 1],
    1
]

流程視角

接下來，我們站在過程視角，檢視這道面試題。首先，它的流程可以分為兩個步驟：1）取得前N行楊輝三角的資料；2）依照圖示對齊的方式列印。

第一步，基於我們前面對資料的分析，可以輕易的得出對應的方法設計：

function yanghui_datas($n); // 获取前N行杨辉三角数据
function yanghui_line_datas($prev_line_data); // 依据前一行数据获取下一行数据

第二步，依據圖示對齊方式進行列印。單純的列印是很簡單的，所以，關鍵在於「對齊」。

解決對齊的方法，無非就是留白給對應的位置。但我們發現，該怎麼留白是不清楚的。那就進一步思考，導致留白邏輯不清晰的困難問題是什麼？

透過分析，可以看到，如果只需要輸出前5行，那麼每個數字都是個位數，如果要輸出第6行，那就開始有十位數。因此，是數字寬度的不確定性，產生了這裡的困難。

逆向思維，如果數字的寬度確定，那就沒有這個困難。所以：

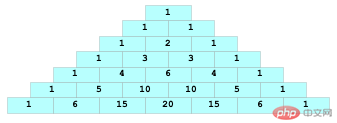
我們把每個數字放到一個等寬的格子裡。這樣，整個問題就清晰了：

格子宽度 = 最大数字宽度 + 1
行前留白 = (LINE_COUNT - LINE_NO) * 格子宽度 / 2
格子内部: (数字居中)
左留白 = (格子宽度 - 数字宽度)  / 2
右留白 = 格子宽度 - 左留白 - 数字宽度

經過上面的分析，程式碼幾乎就躍然紙上了。

// 获取前N行杨辉三角数据
function yanghui_datas($n_line) {
    $datas = []; 
    $prev_line_datas = []; 
    while ($n_line -- > 0) {
        $line_datas = yanghui_line_datas($prev_line_datas);
        array_push($datas, $line_datas);
        $prev_line_datas = $line_datas;
    }   
    return $datas;
}
// 通过前一行数据获取下一行数据
function yanghui_line_datas($prev_line_datas) {
    if (empty($prev_line_datas)) {
        return [1];
    }   
    $line_datas = []; 
    array_push($line_datas, 1); // 行首
    for ($i = 1; $i < count($prev_line_datas); $i ++) {
        array_push($line_datas, $prev_line_datas[$i - 1] + $prev_line_datas[$i]);
    }   
    array_push($line_datas, 1); // 行尾
    return $line_datas;
}
// 打印指定的杨辉三角数据
function yanghui_print($datas) {
    $space         = &#39; &#39;; // 留白字符
    $newline       = &#39;<br />&#39;; // 换行符
    $max_num       = yanghui_max_num($datas); // 最大数字
    $max_num_width = yanghui_num_width($max_num); // 最大宽度
    $unit_width    = $max_num_width + 1; // 格子宽度
    $line_count    = count($datas); // 行数
    foreach ($datas as $idx => $line_datas) {
        $line_no           = $idx + 1; // 行号
        $line_prefix_width = ($line_count - $line_no) * $unit_width / 2; // 行前留白数
        echo str_repeat($space, $line_prefix_width);
        foreach ($line_datas as $num) {
            $num_width   = yanghui_num_width($num); // 数字宽度
            $left_width  = intval(($unit_width - $num_width) / 2); // 格子内左留白宽度
            $right_width = $unit_width - $left_width - $num_width; // 格子内右留白宽度
            echo str_repeat($space, $left_width);
            echo $num;
            echo str_repeat($space, $right_width);
        }
        echo $newline;
    }
}
// 获取最大数
function yanghui_max_num($datas) {
    $max = 0;
    foreach ($datas as $line_datas) {
        foreach ($line_datas as $num) {
            $max = max($max, $num);
        }   
    }   
    return $max;
}
// 获取数字的宽度
function yanghui_num_width($num) {
    return strlen(strval($num));
}

最後，過程的兩個部分組裝起來，就是想要的結果。

function yanghui_dump($n) {
    $datas = yanghui_datas($n);
    yanghui_print($datas);
}

補充

有人說，楊輝三角中的數字，可以依據座標直接計算得到，沒關係，替換掉獲取資料的對應部分即可。

啟示

當我們面對問題時，有兩種思考模式：經驗型和能力型。

經驗型思維，搜尋自己的知識庫，發現楊輝三角應該要一個兩層循環，就開始執行；執行了一步之後，發現卡住了，下一個問題自己的知識庫中沒有，然後就陷入了沉思！

能力型思維，先分析問題的本質構成，對問題進行分解，將複雜的大問題轉換成多個簡單的小問題，抽絲剝繭，在自己的知識庫中搜尋每個小問題的答案，最終解決問題。

兩種思維模式的優劣勢顯而易見，經驗型思維適合解決確定的、已知的、簡單的問題，效率更高；能力型思維適合解決不確定的、未知的、複雜的問題，適應性更廣。

透過程式設計鍛鍊能力型思維

程式設計，是一項極富創造力，注重邏輯和推演的工作。

當我們開始程式設計之前，首先需要站在具體問題的層面，對目標系統進行分析，然後，又需要站在抽象視角層面，把目標系統拔高一層進行演繹。在具體與抽象之間，不斷的推敲，找到合理的對現實的抽象描述。

這個分析推演的過程，就是尋找事物本質的過程。只不過，我們的日常工作，面對大量繁雜的需求，沒有過多的時間進行設計層面的思考。現實，把我們磨成了需求翻譯機器。

大部分程式設計師其實不甘於此，所以，我想透過一份教程，幫助有意願尋求改變的同學，促進這種改變的達成。

2014年，我寫了目前公司使用的框架，已經穩定運作超過5年，支撐了超過60萬行業務程式碼，但它本身只有6000行程式碼。接下來一段時間，我會以它為藍本，站在重新編寫一個框架的角度上，全面的複現編寫框架的思考、分析、設計、實現整個過程，並將其整理為一份視頻教程，以期能幫助大家找到程式設計的感覺。 （自願付費，可自由分享與傳播）

整個教程大致分12講，每講有一個獨立的主題，每講時間1-3小時不等，並配以一篇公眾號文章發布。大的層面架構分為3個部分：與外部環境的互動、對業務層的封裝限制、ORM之類的輔助工具。

教程

因文字表現力有限，本文僅作為一個引子，具體關於職業發展的分析、教程想要傳遞的價值、以及傳遞價值採用的方法，請下載視頻教程深入學習。

【十年一劍，透過框架理解抽象思維】是我錄製的一套系列教程，透過重現開發一套框架的思考、分析、設計、實現全過程，幫助大家尋找程序設計的靈感（自願付費，可自由傳播分享）。教學課程會透過公眾號《抽象思維》發布。

今天發布的是第一講《錄製教程的意義》，感興趣想要深入學習的同學，請掃碼下載視頻教程(地址: https://pan.baidu.com /wap/init?surl=IZ24Az5GFpQoQSD4WbfR8g  提取密碼：rcga)

以上是程式設計師，你還能幹幾年？的詳細內容。更多資訊請關注PHP中文網其他相關文章！