JS實作堆疊排序
- 不言原創
- 2018-07-07 17:50:382140瀏覽
這篇文章主要介紹了關於JS實現堆排序,有著一定的參考價值,現在分享給大家,有需要的朋友可以參考一下
堆的預備知識
堆是一個完全二元樹。
完全二元樹: 二元樹除開最後一層,其他層結點數都達到最大,最後一層的所有結點都集中在左邊(左邊結點排列滿的情況下,右邊才能缺結點)。
大頂堆:根結點為最大值,每個結點的值大於或等於其孩子結點的值。
小頂堆:根結點為最小值,每個結點的值小於或等於其孩子結點的值。
堆的儲存: 堆由陣列來實現,相當於對二元樹做層序遍歷。如下圖:


#對於結點i ,其子結點為2i 1 與2i 2 。
堆排序演算法
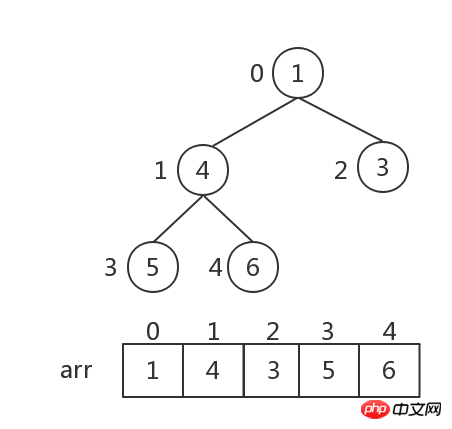
現在需要對如上二元樹做升序排序,總共分成三個步驟:
將初始二元樹轉換為大頂堆(heapify),此時根結點為最大值,將其與最後一個結點交換。
除開最後一個結點,將其餘節點組成的新堆轉換為大頂堆,此時根結點為次最大值,將其與最後一個結點交換。
重複步驟2,直到堆中元素個數為1(或其對應陣列的長度為1),排序完成。
下面詳細圖解這個過程:
步驟1:
初始化大頂堆,首先選取最後一個非葉子結點(我們只需要調整父節點和孩子節點之間的大小關係,葉子結點之間的大小關係無需調整)。設數組為arr,則第一個非葉結點的下標為:i = Math.floor(arr.length/2 - 1) = 1,也就是數字4,如圖中虛線框,找出三個數字的最大值,與父節點交換。
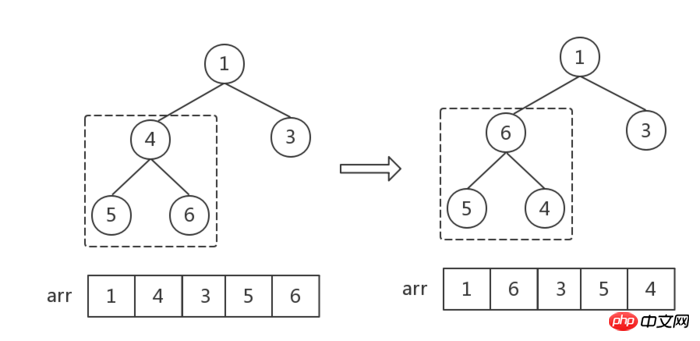
然後,下標 i 依序減1(即從第一個非葉子結點開始,從右至左,從下至上遍歷所有非葉子節點)。後面的每一次調整都是如此:找到父子結點中的最大值,做交換。
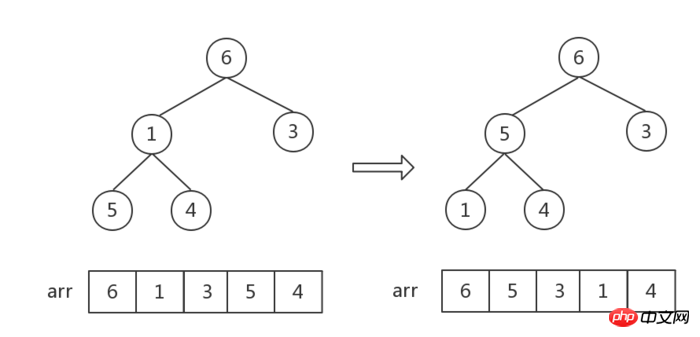
這一步驟中數字6、1交換後,數字[1,5,4]組成的堆順序不對,需要執行一步調整。因此需要注意,每次調整一個非葉子結點後,都要觀察是否會影響子堆順序!
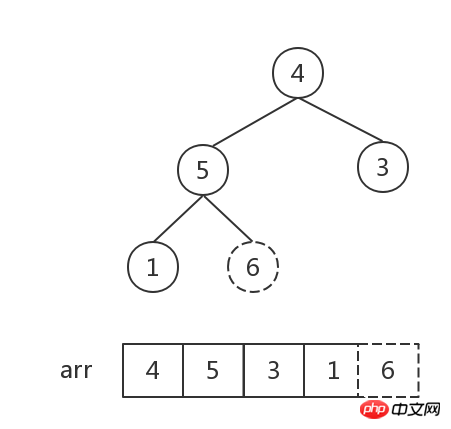
這次調整後,根節點為最大值,形成了一個大頂堆,將根節點與最後一個結點交換。
步驟2:
除開目前最後一個結點6(即最大值),將其餘結點[4,5,3,1]組成新堆轉化為大頂堆(注意觀察,此時根節點以外的其他結點,都滿足大頂堆的特徵,所以可以從根節點4開始調整,即找到4應該處於的位置即可)。
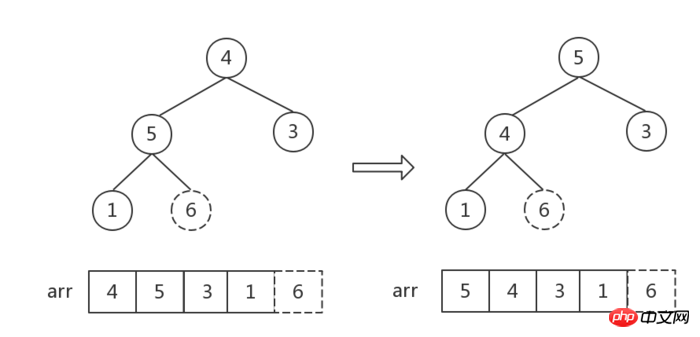
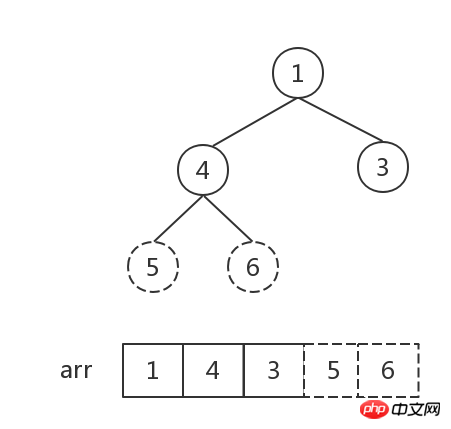
#步驟3:
接下來重複執行步驟2,直到堆中元素個數為1:
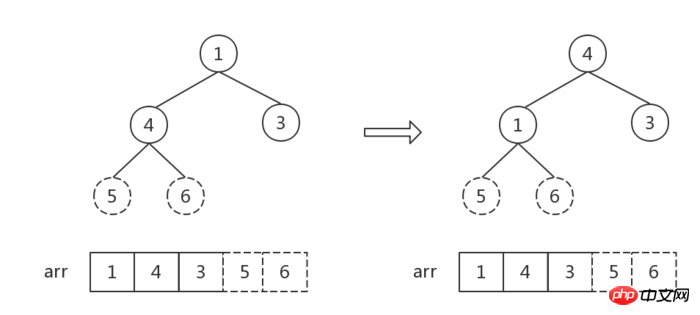
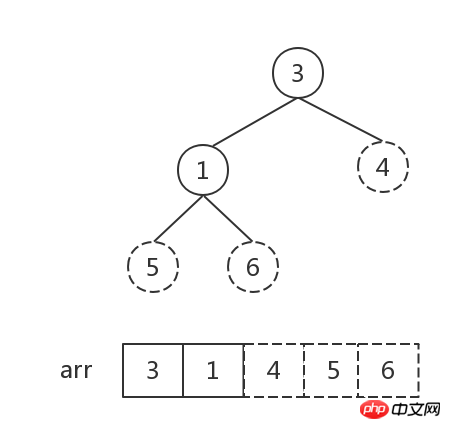
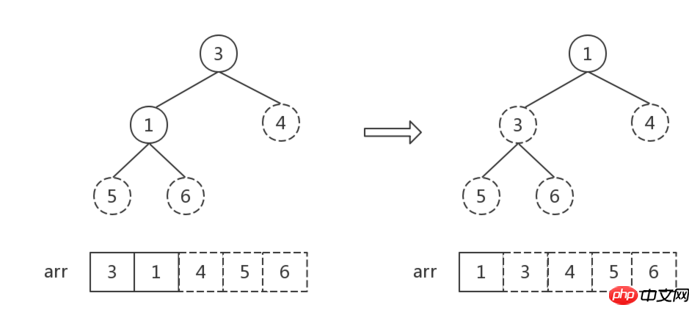
#堆中元素個數為1, 排序完成。
JavaScript實作
// 交换两个节点
function swap(A, i, j) {
let temp = A[i];
A[i] = A[j];
A[j] = temp;
}
// 将 i 结点以下的堆整理为大顶堆,注意这一步实现的基础实际上是:
// 假设 结点 i 以下的子堆已经是一个大顶堆,adjustheap 函数实现的
// 功能是实际上是:找到 结点 i 在包括结点 i 的堆中的正确位置。后面
// 将写一个 for 循环,从第一个非叶子结点开始,对每一个非叶子结点
// 都执行 adjustheap 操作,所以就满足了结点 i 以下的子堆已经是一大
//顶堆
function adjustHeap(A, i, length) {
let temp = A[i]; // 当前父节点
// j<length function>=0; i--) {
adjustHeap(A, i, A.length);
}
// 排序,每一次for循环找出一个当前最大值,数组长度减一
for(let i = Math.floor(A.length-1); i>0; i--) {
swap(A, 0, i); // 根节点与最后一个节点交换
adjustHeap(A, 0, i); // 从根节点开始调整,并且最后一个结点已经为当
// 前最大值,不需要再参与比较,所以第三个参数
// 为 i,即比较到最后一个结点前一个即可
}
}
let Arr = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
heapSort(Arr);
alert(Arr);</length>
程式註解: 將i 結點以下的堆整理為大頂堆,注意這一步實現的基礎其實是:假設結點i 以下的子堆已經是一個大頂堆,adjustHeap 函數實現的功能是實際上是:找到結點i 在包含結點i 的堆中的正確位置。後面做第一次堆化時,heapSort 中寫了一個for 循環,從第一個非葉子結點開始,對每一個非葉子結點都執行adjustHeap 操作,所以就滿足了每一次adjustHeap 中,結點i 以下的子堆已經是一大頂堆。
複雜度分析:adjustHeap 函數中相當於堆的每一層只遍歷一個結點,因為
具有n個結點的完全二叉樹的深度為[log2n] 1,所以adjustHeap 的複雜度為O(logn),而外層循環共有f(n) 次,所以最終的複雜度為O(nlogn)。
堆的應用
堆主要是用來實作優先權佇列,以下是優先權佇列的應用範例:
作業系統動態選擇優先權最高的任務執行。
靜態問題中,在N個元素中選出前M名,使用排序的複雜度:O(NlogN),使用優先隊列的複雜度: O(NlogM)。
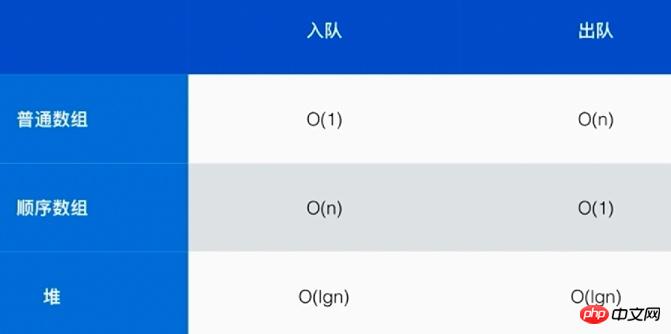
而實作優先佇列採用普通陣列、順序陣列和堆疊的不同複雜度如下:
以上是JS實作堆疊排序的詳細內容。更多資訊請關注PHP中文網其他相關文章!

