Python是演算法應用實戰之棧

堆疊是什麼，你可以理解為一種先入後出的資料結構（First In Last Out），一種操作受限的線性表。以下這篇文章主要跟大家介紹了Python中棧的應用實戰，文中給了多個實例，需要的朋友可以參考借鑒，下面來一起看看吧。

堆疊(stack)

堆疊又稱之為堆疊是一個特殊的有序表，其插入和刪除操作都在堆疊頂進行操作，並且按照先進後出，後進先出的規則進行運作。

如下圖

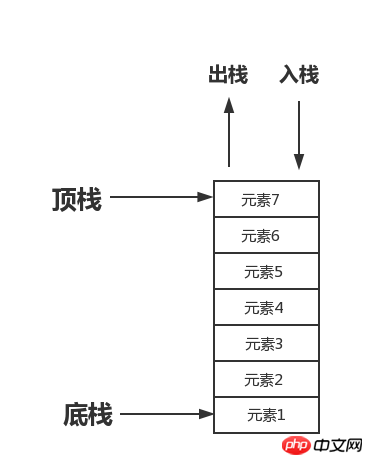
例如槍的彈匣，第一顆放進彈匣的子彈反而在發射出去的時候是最後一個，而最後放入彈匣的子彈在打出去的時候是第一顆發射出去的。

堆疊的介面

如果你建立了一個堆疊，那麼應該具有以下介面來進行對堆疊的操作

##isEmpty()判斷是否為空堆疊length()取得堆疊的長度##getTop()知道堆疊需要上述的介面後，那麼在Python中，列表就類似是一個棧，提供介面如下：

介面	描述
push()	入堆疊
pop()	出堆疊
取棧頂的元素，元素不​​出棧

操作s = []s.append(x)s.pop()#not slen(s)s[-1]

#描述
建立一個堆疊
在堆疊內新增一個元素
在堆疊內刪除一個元素
判斷是否為空堆疊
取得堆疊內元素的數量
取得棧頂的元素

Python中的堆疊介面使用實例：##

# 创建一个栈
In [1]: s = []
# 往栈内添加一个元素
In [2]: s.append(1)
In [3]: s
Out[3]: [1]
# 删除栈内的一个元素
In [4]: s.pop()
Out[4]: 1
In [5]: s
Out[5]: []
# 判断栈是否为空
In [6]: not s
Out[6]: True
In [7]: s.append(1)
In [8]: not s
Out[8]: False
# 获取栈内元素的数量
In [9]: len(s)
Out[9]: 1
In [10]: s.append(2)
In [11]: s.append(3)
# 取栈顶的元素
In [12]: s[-1]
Out[12]: 3

一大波實例

在了解堆疊的基本概念之後，讓我們再來看幾個實例，以便於理解堆疊。

括號符合

題目

假如表達式中允許包含三中括號()、[]、{}，其嵌套順序是任意的，例如：

正確的格式

{()[()]},[{({})}]

#錯誤的格式

##

[(]),[()),(()}

寫一個函數，判斷一個表達式字串，括號匹配是否正確

思路

建立一個空棧，用來儲存尚未找到的左括號；

1. 便利字串，遇到左括號則壓棧，遇到右括號則出棧一個左括號進行比對；

2. 在第二步驟過程中，如果空棧情況下遇到右括號，表示缺少左括號，不符；

3. 在第二步遍歷結束時，堆疊不為空，說明缺少右括號，不匹配；

4. 解決程式碼

#建議在pycharm中打斷點，以便於更好的理解

#!/use/bin/env python
# _*_ coding:utf-8 _*_
LEFT = {'(', '[', '{'} # 左括号
RIGHT = {')', ']', '}'} # 右括号
def match(expr):
 """
 :param expr: 传过来的字符串
 :return: 返回是否是正确的
 """
 stack = [] # 创建一个栈
 for brackets in expr: # 迭代传过来的所有字符串
 if brackets in LEFT: # 如果当前字符在左括号内
  stack.append(brackets) # 把当前左括号入栈
 elif brackets in RIGHT: # 如果是右括号
  if not stack or not 1 <= ord(brackets) - ord(stack[-1]) <= 2:
  # 如果当前栈为空，()]
  # 如果右括号减去左括号的值不是小于等于2大于等于1
  return False # 返回False
  stack.pop() # 删除左括号
 return not stack # 如果栈内没有值则返回True，否则返回False
result = match(&#39;[(){()}]&#39;)
print(result)

迷宮問題

題目用一個二維陣列表示一個簡單的迷宮，用0表示通路，用1表示阻斷，老鼠在每個點上可以移動相鄰的東南西北四個點，設計一個演算法，模擬老鼠走迷宮，找到從入口到出口的一條路徑。

如圖所示

出去的正確線路如圖中的紅線所示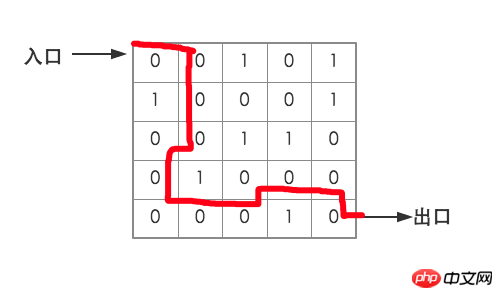

思路

用一個堆疊來記錄老鼠從入口到出口的路徑

1. 走到某點後，將該點左邊壓棧，並把該點值置為1 ，表示走過了；

2. 從臨近的四個點中可到達的點中任意選取一個，走到該點；

3. # #如果在到達某點後臨近的4個點都不走，表示已經走入死胡同，此時退棧，退回一步嘗試其他點；

4. 反复執行第二、三、四步驟直到找到出口；

5. 解決程式碼

#

#!/use/bin/env python
# _*_ coding:utf-8 _*_
def initMaze():
 """
 :return: 初始化迷宫
 """
 maze = [[0] * 7 for _ in range(5 + 2)] # 用列表解析创建一个7*7的二维数组，为了确保迷宫四周都是墙
 walls = [ # 记录了墙的位置
 (1, 3),
 (2, 1), (2, 5),
 (3, 3), (3, 4),
 (4, 2), # (4, 3), # 如果把(4, 3)点也设置为墙，那么整个迷宫是走不出去的，所以会返回一个空列表
 (5, 4)
 ]
 for i in range(7): # 把迷宫的四周设置成墙
 maze[i][0] = maze[i][-1] = 1
 maze[0][i] = maze[-1][i] = 1
 for i, j in walls: # 把所有墙的点设置为1
 maze[i][j] = 1
 return maze
"""
[1, 1, 1, 1, 1, 1, 1]
[1, 0, 0, 1, 0, 0, 1]
[1, 1, 0, 0, 0, 1, 1]
[1, 0, 0, 1, 1, 0, 1]
[1, 0, 1, 0, 0, 0, 1]
[1, 0, 0, 0, 1, 0, 1]
[1, 1, 1, 1, 1, 1, 1]
"""
def path(maze, start, end):
 """
 :param maze: 迷宫
 :param start: 起始点
 :param end: 结束点
 :return: 行走的每个点
 """
 i, j = start # 分解起始点的坐标
 ei, ej = end # 分解结束点的左边
 stack = [(i, j)] # 创建一个栈，并让老鼠站到起始点的位置
 maze[i][j] = 1 # 走过的路置为1
 while stack: # 栈不为空的时候继续走，否则退出
 i, j = stack[-1] # 获取当前老鼠所站的位置点
 if (i, j) == (ei, ej): break # 如果老鼠找到了出口
 for di, dj in [(0, -1), (0, 1), (-1, 0), (1, 0)]: # 左右上下
  if maze[i + di][j + dj] == 0: # 如果当前点可走
  maze[i + di][j + dj] = 1 # 把当前点置为1
  stack.append((i + di, j + dj)) # 把当前的位置添加到栈里面
  break
 else: # 如果所有的点都不可走
  stack.pop() # 退回上一步
 return stack # 如果迷宫不能走则返回空栈
Maze = initMaze() # 初始化迷宫
result = path(maze=Maze, start=(1, 1), end=(5, 5)) # 老鼠开始走迷宫
print(result)
# [(1, 1), (1, 2), (2, 2), (3, 2), (3, 1), (4, 1), (5, 1), (5, 2), (5, 3), (4, 3), (4, 4), (4, 5), (5, 5)]

後綴表達式求值

題目

計算一個表達式時，編譯器通常使用後綴表達式，這種表達式不需要括號：

中綴表達式

後綴表達式#2 3 * 42 3 4 * ( 1 2 ) * ( 6 / 3 ) 21 2 6 3 / * 2 18 / ( 3 * ( 1 2 ) )18 3 1 2 * /

编写程序实现后缀表达式求值函数。

思路

1. 建立一个栈来存储待计算的操作数；

2. 遍历字符串，遇到操作数则压入栈中，遇到操作符号则出栈操作数(n次)，进行相应的计算，计算结果是新的操作数压回栈中，等待计算

3. 按上述过程，遍历完整个表达式，栈中只剩下最终结果；
   

解决代码

#!/use/bin/env python
# _*_ coding:utf-8 _*_
operators = { # 运算符操作表
 '+': lambda op1, op2: op1 + op2,
 '-': lambda op1, op2: op1 - op2,
 '*': lambda op1, op2: op1 * op2,
 '/': lambda op1, op2: op1 / op2,
}
def evalPostfix(e):
 """
 :param e: 后缀表达式
 :return: 正常情况下栈内的第一个元素就是计算好之后的值
 """
 tokens = e.split() # 把传过来的后缀表达式切分成列表
 stack = []
 for token in tokens: # 迭代列表中的元素
 if token.isdigit(): # 如果当前元素是数字
  stack.append(int(token)) # 就追加到栈里边
 elif token in operators.keys(): # 如果当前元素是操作符
  f = operators[token] # 获取运算符操作表中对应的lambda表达式
  op2 = stack.pop() # 根据先进后出的原则，先让第二个元素出栈
  op1 = stack.pop() # 在让第一个元素出栈
  stack.append(f(op1, op2)) # 把计算的结果在放入到栈内
 return stack.pop() # 返回栈内的第一个元素
result = evalPostfix('2 3 4 * +')
print(result)
# 14

背包问题

题目

有一个背包能装10kg的物品，现在有6件物品分别为：

物品名称	重量
物品0	1kg
物品1	8kg
物品2	4kg
物品3	3kg
物品4	5kg
物品5	2kg

编写找出所有能将背包装满的解，如物品1+物品5。

解决代码

#!/use/bin/env python
# _*_ coding:utf-8 _*_
def knapsack(t, w):
 """
 :param t: 背包总容量
 :param w: 物品重量列表
 :return:
 """
 n = len(w) # 可选的物品数量
 stack = [] # 创建一个栈
 k = 0 # 当前所选择的物品游标
 while stack or k < n: # 栈不为空或者k<n
 while t > 0 and k < n: # 还有剩余空间并且有物品可装
  if t >= w[k]: # 剩余空间大于等于当前物品重量
  stack.append(k) # 把物品装备背包
  t -= w[k] # 背包空间减少
  k += 1 # 继续向后找
 if t == 0: # 找到了解
  print(stack)
 # 回退过程
 k = stack.pop() # 把最后一个物品拿出来
 t += w[k] # 背包总容量加上w[k]
 k += 1 # 装入下一个物品
knapsack(10, [1, 8, 4, 3, 5, 2])
"""
[0, 2, 3, 5]
[0, 2, 4]
[1, 5]
[3, 4, 5]
"""

以上是Python是演算法應用實戰之棧的詳細內容。更多資訊請關注PHP中文網其他相關文章！