這篇文章主要介紹了python程式設計透過蒙特卡羅法計算定積分詳解,具有一定借鑒價值,需要的朋友可以參考下。
想當初,考研的時候要是知道有這麼好東西,計算定積分。 。 。開玩笑,那時候計算定積分根本沒有這麼簡單的。但這確實給我開啟了一個思路,用程式語言解決更多更複雜的數學問題。下面進入正題。
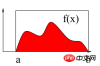
如上圖所示,計算區間[a b]上f(x)的積分即求曲線與X軸圍成紅色區域的面積。以下使用蒙特卡羅法計算區間[2 3]上的定積分:∫(x2 4*x*sin(x))dx
##
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**2 + 4*x*np.sin(x)
def intf(x):
return x**3/3.0+4.0*np.sin(x) - 4.0*x*np.cos(x)
a = 2;
b = 3;
# use N draws
N= 10000
X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b
Y =f(X) # CALCULATE THE f(x)
# 蒙特卡洛法计算定积分:面积=宽度*平均高度
Imc= (b-a) * np.sum(Y)/ N;
exactval=intf(b)-intf(a)
print "Monte Carlo estimation=",Imc, "Exact number=", intf(b)-intf(a)
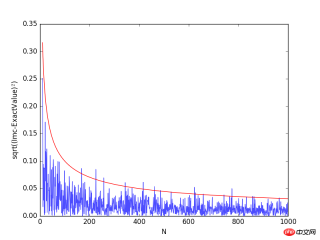
# --How does the accuracy depends on the number of points(samples)? Lets try the same 1-D integral
# The Monte Carlo methods yield approximate answers whose accuracy depends on the number of draws.
Imc=np.zeros(1000)
Na = np.linspace(0,1000,1000)
exactval= intf(b)-intf(a)
for N in np.arange(0,1000):
X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b
Y =f(X) # CALCULATE THE f(x)
Imc[N]= (b-a) * np.sum(Y)/ N;
plt.plot(Na[10:],np.sqrt((Imc[10:]-exactval)**2), alpha=0.7)
plt.plot(Na[10:], 1/np.sqrt(Na[10:]), 'r')
plt.xlabel("N")
plt.ylabel("sqrt((Imc-ExactValue)$^2$)")
plt.show()



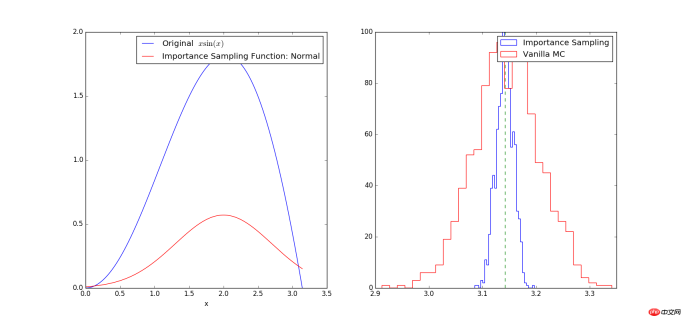
# -*- coding: utf-8 -*- # Example: Calculate ∫sin(x)xdx # The function has a shape that is similar to Gaussian and therefore # we choose here a Gaussian as importance sampling distribution. from scipy import stats from scipy.stats import norm import numpy as np import matplotlib.pyplot as plt mu = 2; sig =.7; f = lambda x: np.sin(x)*x infun = lambda x: np.sin(x)-x*np.cos(x) p = lambda x: (1/np.sqrt(2*np.pi*sig**2))*np.exp(-(x-mu)**2/(2.0*sig**2)) normfun = lambda x: norm.cdf(x-mu, scale=sig) plt.figure(figsize=(18,8)) # set the figure size # range of integration xmax =np.pi xmin =0 # Number of draws N =1000 # Just want to plot the function x=np.linspace(xmin, xmax, 1000) plt.subplot(1,2,1) plt.plot(x, f(x), 'b', label=u'Original $x\sin(x)$') plt.plot(x, p(x), 'r', label=u'Importance Sampling Function: Normal') plt.xlabel('x') plt.legend() # ============================================= # EXACT SOLUTION # ============================================= Iexact = infun(xmax)-infun(xmin) print Iexact # ============================================ # VANILLA MONTE CARLO # ============================================ Ivmc = np.zeros(1000) for k in np.arange(0,1000): x = np.random.uniform(low=xmin, high=xmax, size=N) Ivmc[k] = (xmax-xmin)*np.mean(f(x)) # ============================================ # IMPORTANCE SAMPLING # ============================================ # CHOOSE Gaussian so it similar to the original functions # Importance sampling: choose the random points so that # more points are chosen around the peak, less where the integrand is small. Iis = np.zeros(1000) for k in np.arange(0,1000): # DRAW FROM THE GAUSSIAN: xis~N(mu,sig^2) xis = mu + sig*np.random.randn(N,1); xis = xis[ (xis<xmax) & (xis>xmin)] ; # normalization for gaussian from 0..pi normal = normfun(np.pi)-normfun(0) # 注意:概率密度函数在采样区间[0 pi]上的积分需要等于1 Iis[k] =np.mean(f(xis)/p(xis))*normal # 因此,此处需要乘一个系数即p(x)在[0 pi]上的积分 plt.subplot(1,2,2) plt.hist(Iis,30, histtype='step', label=u'Importance Sampling'); plt.hist(Ivmc, 30, color='r',histtype='step', label=u'Vanilla MC'); plt.vlines(np.pi, 0, 100, color='g', linestyle='dashed') plt.legend() plt.show()
Python程式設計中NotImplementedError的使用方法_python
以上是python程式設計透過蒙特卡羅法計算定積分詳解的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 您如何切成python陣列?May 01, 2025 am 12:18 AM
您如何切成python陣列?May 01, 2025 am 12:18 AMPython列表切片的基本語法是list[start:stop:step]。 1.start是包含的第一個元素索引,2.stop是排除的第一個元素索引,3.step決定元素之間的步長。切片不僅用於提取數據,還可以修改和反轉列表。
 在什麼情況下,列表的表現比數組表現更好?May 01, 2025 am 12:06 AM
在什麼情況下,列表的表現比數組表現更好?May 01, 2025 am 12:06 AMListSoutPerformarRaysin:1)DynamicsizicsizingandFrequentInsertions/刪除,2)儲存的二聚體和3)MemoryFeliceFiceForceforseforsparsedata,butmayhaveslightperformancecostsinclentoperations。
 如何將Python數組轉換為Python列表?May 01, 2025 am 12:05 AM
如何將Python數組轉換為Python列表?May 01, 2025 am 12:05 AMtoConvertapythonarraytoalist,usEthelist()constructororageneratorexpression.1)intimpthearraymoduleandcreateanArray.2)USELIST(ARR)或[XFORXINARR] to ConconverTittoalist,請考慮performorefformanceandmemoryfformanceandmemoryfformienceforlargedAtasetset。
 當Python中存在列表時,使用數組的目的是什麼?May 01, 2025 am 12:04 AM
當Python中存在列表時,使用數組的目的是什麼?May 01, 2025 am 12:04 AMchoosearraysoverlistsinpythonforbetterperformanceandmemoryfliceSpecificScenarios.1)largenumericaldatasets:arraysreducememoryusage.2)績效 - 臨界雜貨:arraysoffersoffersOffersOffersOffersPoostSfoostSforsssfortasssfortaskslikeappensearch orearch.3)testessenforcety:arraysenforce:arraysenforc
 說明如何通過列表和數組的元素迭代。May 01, 2025 am 12:01 AM
說明如何通過列表和數組的元素迭代。May 01, 2025 am 12:01 AM在Python中,可以使用for循環、enumerate和列表推導式遍歷列表;在Java中,可以使用傳統for循環和增強for循環遍歷數組。 1.Python列表遍歷方法包括:for循環、enumerate和列表推導式。 2.Java數組遍歷方法包括:傳統for循環和增強for循環。
 什麼是Python Switch語句?Apr 30, 2025 pm 02:08 PM
什麼是Python Switch語句?Apr 30, 2025 pm 02:08 PM本文討論了版本3.10中介紹的Python的新“匹配”語句,該語句與其他語言相同。它增強了代碼的可讀性,並為傳統的if-elif-el提供了性能優勢
 Python中的功能註釋是什麼?Apr 30, 2025 pm 02:06 PM
Python中的功能註釋是什麼?Apr 30, 2025 pm 02:06 PMPython中的功能註釋將元數據添加到函數中,以進行類型檢查,文檔和IDE支持。它們增強了代碼的可讀性,維護,並且在API開發,數據科學和圖書館創建中至關重要。


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

EditPlus 中文破解版
體積小,語法高亮,不支援程式碼提示功能

PhpStorm Mac 版本
最新(2018.2.1 )專業的PHP整合開發工具

SecLists
SecLists是最終安全測試人員的伙伴。它是一個包含各種類型清單的集合,這些清單在安全評估過程中經常使用,而且都在一個地方。 SecLists透過方便地提供安全測試人員可能需要的所有列表,幫助提高安全測試的效率和生產力。清單類型包括使用者名稱、密碼、URL、模糊測試有效載荷、敏感資料模式、Web shell等等。測試人員只需將此儲存庫拉到新的測試機上,他就可以存取所需的每種類型的清單。

Safe Exam Browser
Safe Exam Browser是一個安全的瀏覽器環境,安全地進行線上考試。該軟體將任何電腦變成一個安全的工作站。它控制對任何實用工具的訪問,並防止學生使用未經授權的資源。

禪工作室 13.0.1
強大的PHP整合開發環境






