首頁 > 文章 > 後端開發 > PHP排序演算法之堆排序(Heap Sort)

PHP排序演算法之堆排序(Heap Sort)

不言原創: 2018-04-21 14:17:252076瀏覽

這篇文章主要介紹了PHP排序演算法之堆排序(Heap Sort),結合實例形式詳細分析了堆排序的原理、實作方法及相關使用注意事項,需要的朋友可以參考下

本文實例敘述了PHP排序演算法之堆排序(Heap Sort)。分享給大家供大家參考，具體如下：

演算法引進：

在這裡我直接引用《大話資料結構》裡面的開頭：

在前面講到簡單選擇排序，它在待排序的n 個記錄中選擇一個最小的記錄需要比較n - 1 次，本來這也可以理解，查找第一個數據需要比較這麼多次是正常的，否則如何知道他是最小的記錄。

可惜的是，這樣的操作並沒有把每一趟的比較結果保存下來，在後一趟的比較重，有許多比較在前一趟已經做過了，但由於前一趟排序時未儲存這些比較結果，所以後一趟排序時又重複執行了這些比較操作，因而記錄的比較次數較多。

如果可以做到每次在選擇到最小記錄的同時，並根據比較結果對其他記錄做出相應的調整，那樣排序的總體效率就會非常高了。而堆排序，就是對簡單選擇排序的一種改進，這種改進的效果是非常明顯的。

基本概念：

在介紹堆排序之前，我們先來介紹一下堆：

《大話資料結構》裡的定義：堆是具有下列性質的完全二元樹：每個節點的值都大於或等於其左右孩子節點的值，成為大頂堆（大根堆）；或者每個節點的值都小於或等於其左右節點的值，成為小頂堆（小根堆）。

當時我在看到這裡的時候也對有「堆是否是完全二叉樹」有過疑問，網上也有說不是完全二叉樹的，但是無論堆是不是完全二叉樹，尚且保留意見。我們只要知道，在這裡我們採用完全二元樹形式的大根堆（小跟堆），主要是為了方便儲存和計算（後面我們會看到帶來的便利）。

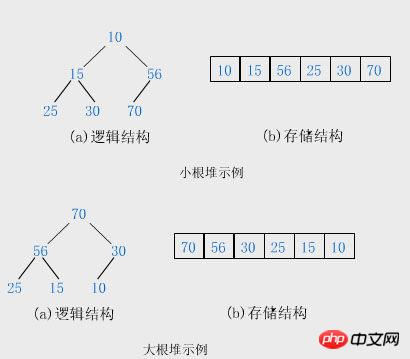
堆排序演算法：

堆排序就是利用堆（假設利用大根堆）進行排序的方法，它的基本思想是：將待排序的序列建構成一個大根堆。此時，整個序列的最大值就是堆頂的根節點。將它移走（其實就是將其與堆數組的末尾元素交換，此時末尾元素就是最大值），然後將剩餘的n - 1 個序列重新構造成一個堆，這樣就會得到n 個元素中的次小的值。如此反覆執行，便能得到一個有序序列了。

大根堆排序演算法的基本操作：

#①建堆，建堆是不斷調整堆的過程，從len/2 開始調整，一直到第一個節點，此處len 是堆中元素的數量。建堆的過程是線性的過程，從len/2 到0 處一直呼叫調整堆的過程，相當於o(h1) o(h2) … o(hlen/2) 其中h 表示節點的深度， len/2表示節點的個數，這是一個求和的過程，結果是線性的O(n)。

②調整堆：調整堆在建構堆的過程中會用到，在堆排序過程中也會用到。利用的想法是比較節點i和它的孩子節點left(i) , right(i)，選出三者最大(或最小)者，如果最大（小）值不是節點i而是它的一個孩子節點，那邊交互節點i和該節點，然後再呼叫調整堆過程，這是一個遞歸的過程。調整堆的過程時間複雜度與堆的深度有關係，是 lgn 的操作，因為是沿著深度方向進行調整的。

③堆排序：堆排序是利用上面的兩個過程來進行的。首先是根據元素來建構堆。然後將堆的根節點取出(一般是與最後一個節點進行交換)，將前面 len-1 個節點繼續進行堆調整的過程，然後再將根節點取出，這樣一直到所有節點都取出。堆排序過程的時間複雜度是 O(nlgn)。因為建堆的時間複雜度是 O(n)（調用一次）；調整堆的時間複雜度是 lgn，呼叫了 n-1 次，所以堆排序的時間複雜度是 O(nlgn)。

在這個過程中是需要大量的圖示才能看的明白的，但是我懶。。。。。。

演算法實作：

<?php
//堆排序（对简单选择排序的改进）
function swap(array &$arr,$a,$b){
  $temp = $arr[$a];
  $arr[$a] = $arr[$b];
  $arr[$b] = $temp;
}
//调整 $arr[$start]的关键字，使$arr[$start]、$arr[$start+1]、、、$arr[$end]成为一个大根堆（根节点最大的完全二叉树）
//注意这里节点 s 的左右孩子是 2*s + 1 和 2*s+2 （数组开始下标为 0 时）
function HeapAdjust(array &$arr,$start,$end){
  $temp = $arr[$start];
  //沿关键字较大的孩子节点向下筛选
  //左右孩子计算（我这里数组开始下标识 0）
  //左孩子2 * $start + 1，右孩子2 * $start + 2
  for($j = 2 * $start + 1;$j <= $end;$j = 2 * $j + 1){
    if($j != $end && $arr[$j] < $arr[$j + 1]){
      $j ++; //转化为右孩子
    }
    if($temp >= $arr[$j]){
      break; //已经满足大根堆
    }
    //将根节点设置为子节点的较大值
    $arr[$start] = $arr[$j];
    //继续往下
    $start = $j;
  }
  $arr[$start] = $temp;
}
function HeapSort(array &$arr){
  $count = count($arr);
  //先将数组构造成大根堆（由于是完全二叉树，所以这里用floor($count/2)-1，下标小于或等于这数的节点都是有孩子的节点)
  for($i = floor($count / 2) - 1;$i >= 0;$i --){
    HeapAdjust($arr,$i,$count);
  }
  for($i = $count - 1;$i >= 0;$i --){
    //将堆顶元素与最后一个元素交换，获取到最大元素（交换后的最后一个元素），将最大元素放到数组末尾
    swap($arr,0,$i);
    //经过交换，将最后一个元素（最大元素）脱离大根堆，并将未经排序的新树($arr[0...$i-1])重新调整为大根堆
    HeapAdjust($arr,0,$i - 1);
  }
}
$arr = array(9,1,5,8,3,7,4,6,2);
HeapSort($arr);
var_dump($arr);

執行結果：

array(9) {
 [0]=>
 int(1)
 [1]=>
 int(2)
 [2]=>
 int(3)
 [3]=>
 int(4)
 [4]=>
 int(5)
 [5]=>
 int(6)
 [6]=>
 int(7)
 [7]=>
 int(8)
 [8]=>
 int(9)
}

時間複雜度分析：

它的運行時間只要是消耗在初始建置對和在重建堆屎的反覆篩選上。

整體來說，堆排序的時間複雜度是 O(nlogn)。由於堆排序對原始記錄的排序狀態並不敏感，因此它無論是最好、最差和平均時間複雜度都是 O(nlogn)。這在性能上顯然要遠遠好於冒泡、簡單選擇、直接插入的 O(n^2) 的時間複雜度了。

堆排序是一種不穩定排序方法。

本文參考自《大話資料結構》，在此僅作記錄，方便以後查閱，大神勿噴！

PHP排序演算法之堆排序(Heap Sort)

相關文章