解決Python基於回溯法子集樹模板實現8皇后問題

這篇文章主要介紹了Python基於回溯法子集樹模板實現8皇后問題,簡單說明了8皇后問題的原理並結合實例形式分析了Python回溯法子集樹模板解決8皇后問題的具體實現技巧,需要的朋友可以參考下

本文實例講述了Python基於回溯法子集樹模板實現8皇后問題。分享給大家供大家參考，具體如下：

問題

8×8格的西洋棋上擺放八個皇后，使其不能互相攻擊，即任兩個皇后都不能處於同一行、同一列或同一斜線上，問有多少種擺法。

分析

為了簡化問題，考慮到8個皇后不同行，則每一行放置一個皇后，每一行的皇后可以放置於第0、1、2、...、7列，我們認為每一行的皇后有8種狀態。那麼，我們只要套用子集樹模板，從第0行開始，自上而下，對每一行的皇后，遍歷它的8個狀態即可。

程式碼：

'''
8皇后问题
'''
n = 8 
x = [] # 一个解（n元数组）
X = [] # 一组解
# 冲突检测：判断 x[k] 是否与前 x[0~k-1] 冲突
def conflict(k):
 global x
 for i in range(k):        # 遍历前 x[0~k-1]
  if x[i]==x[k] or abs(x[i]-x[k])==abs(i-k): # 判断是否与 x[k] 冲突
   return True
 return False
# 套用子集树模板
def queens(k): # 到达第k行
 global n, x, X
 if k >= n:   # 超出最底行
  #print(x)
  X.append(x[:]) # 保存（一个解），注意x[:]
 else:
  for i in range(n): # 遍历第 0~n-1 列（即n个状态）
   x.append(i)  # 皇后置于第i列，入栈
   if not conflict(k): # 剪枝
    queens(k+1)
   x.pop()   # 回溯，出栈
# 解的可视化（根据一个解x，复原棋盘。'X'表示皇后）
def show(x):
 global n
 for i in range(n):
  print('. ' * (x[i]) + 'X ' + '. '*(n-x[i]-1))
# 测试
queens(0) # 从第0行开始
print(X[-1], '\n')
show(X[-1])

效果圖

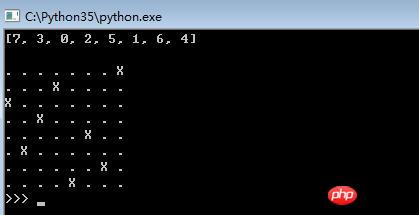
以上是解決Python基於回溯法子集樹模板實現8皇后問題的詳細內容。更多資訊請關注PHP中文網其他相關文章！