Java中的二進位及位元運算詳解

1.表示方法： 　

在Java語言中，二進位數使用補碼表示，最高位元為符號位，正數的符號位元為0，負數為1。補碼的表示需要滿足以下要求。 　

(1)正數的最高位元為0，其餘各位代表數值本身(二進位數)。 　

(2)對於負數，透過對該數絕對值的補碼按位取反，再對整個數加1。

2.位元運算子 　

位元運算表達式由運算元和位元運算子組成，實作對整數型別的二進制數進行位元運算。位元運算子可以分為邏輯運算子(包括~、＆、|和^)及移位運算子(包括>>、<<和>>>)。 

1)左移位運算子（<<）能將運算子左邊的運算物件向左移動運算子右邊指定的位元數（在低位元補0）。 

2)「有符號」右移位運算子（>>）則將運算子左邊的運算物件向右移動運算子右邊指定的位數。 「有符號」右移位運算子使用了「符號擴展」：若值為正，則在高位插入0；若值為負，則在高位插入1。

3)Java也加入了一個「無符號」右移位運算子（>>>），它使用了「零擴充」：無論正負，都在高位插入0。這一運算子是C或C++沒有的。 

4)若對char，byte或short進行移位處理，那麼在移位進行之前，它們會自動轉換成一個int。 只有右邊的5個低位才會用到。這樣可防止我們在一個int數裡移動不切實際的位數。 若對一個long值進行處理，最後得到的結果也是long。此時只會用到右邊的6個低位，防止移動超過long值裡現成的位數。 但在進行「無符號」右移位時，也可能遇到一個問題。若對byte或short值進行右移位運算，得到的可能不是正確的結果（Java 1.0和Java 1.1特別突出）。 它們會自動轉換成int類型，並進行右移位。但「零擴展」不會發生，所以在那些情況下會得到-1的結果。 

　二進位是計算技術中廣泛採用的數制。二進位資料是用0和1兩個數位來表示的數。它的基數為2，進位規則是“逢二進一”，借位規則是“借一當二”，由18世紀德國數理哲學大師萊布尼茲發現。目前的電腦系統使用的基本上是二進位系統，資料在電腦中主要是以補碼的形式儲存的。電腦中的二進位則是一個非常微小的開關，用「開」來表示1，「關」來表示0。

　　那麼Java中的二進位又是怎麼樣的呢？讓我們一起來揭開它神秘的面紗吧。

---

一、Java內建的進位轉換

有關十進位轉為二進位，和二進位轉為十進位這種基本的運算方法這裡就不展開講了。

在Java中內建了幾個方法來幫助我們進行各種進位的轉換。如下圖所示（以Integer整形為例，其他類型雷同）：

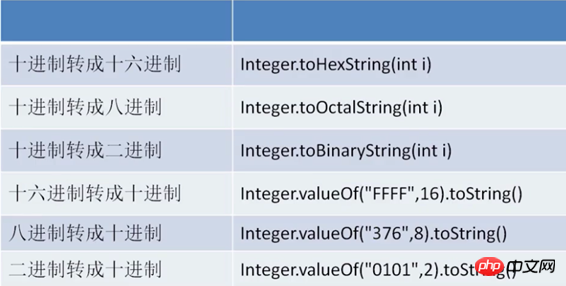
#1，十進位轉換為其他進位：

1 二进制：Integer.toHexString(int i);2 八进制：Integer.toOctalString(int i);3 十六进制：Integer.toBinaryString(int i);

2,其他進位轉換為十進位：

1 二进制：Integer.valueOf("0101",2).toString;2 八进制：Integer.valueOf("376",8).toString;3 十六进制：Integer.valueOf("FFFF",16).toString;

3,使用Integer類別中的parseInt()方法和valueOf()方法都可以將其他進位轉換為10進位。

不同的是parseInt()方法的回傳值是int類型，而valueOf()傳回值是Integer物件。

---

二、基本的位元運算

二進位可以和十進位一樣加減乘除，但是它還有更簡單的運算方式就是－位元運算。例如在計算機中int型別的大小是32bit，可以用32位的二進制數來表示，所以我們可以用位元運算來對int型別的數值進行計算，當然你也可以用平常的方法來計算一些數據，這裡我主要為大家介紹位運算的方法。我們會發現位元運算有著普通運算方法不可比擬的力量。 更多位元運算應用請轉移到我下篇部落格文章《神奇的位元運算》

首先，看一下位元運算的基本運算子：

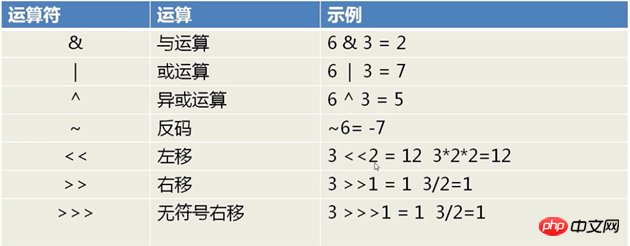
優點：

• #特定情況下，計算方便，速度快，被支援面廣

• #如果用算數方法，速度慢，邏輯複雜

• 位元運算不限於一種語言，它是電腦的基本運算方法

#>>>> >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

（一）由位元與&

兩位全為1，結果才為1

0&0=0；0&1= 0；1&0=0；1&1=1

例如：51&5 即0011 0011 & 0000 0101 =0000 0001 因此51&5=1.

特殊用法

（1）清零。 如果想要將一個單元清零，即使其全部二進位位元為0，只要與一個各位都是零的數值相與，結果為零。

（2）取一個數字中指定位元。

例如：設X=10101110，取X的低四位，用X&0000 1111=0000 1110即可得到。

方法：找一個數，對應x要取的位，該數的對應位為1，其餘位為零，此數與x進行「與運算」可以得到x中的指定位。

（二）位元或 |

只要有一個為1，結果就為1。

0|0=0; 0|1=1；1|0=1；1|1=1;

例如：51|5 即0011 0011 | 0000 0101 =0011 0111 因此51|5=55

 特殊用法

常用來對一個資料的某些位置1。

方法：求一個數，對應x要置1的位，數的對應位為1，其餘位為零。此數與x相或可使x中的某些位置1。

（三）異或^

兩個對應位元為「異」（值不同），則該位元結果為1，否則為0

0^0=0; 0^1=1; 1^0=1; 1^1=0;

例如：51^5 即0011 0011 ^ 0000 0101 =0011 0110 因此51^ 5=54

特殊用法

（1）  與1相異或，使特定位元翻轉

方法：找一個數，對應X要翻轉的位，該數的對應為1，其餘位為零，此數與X對應位異或即可。

例如：X=1010 1110，使X低四位翻轉，用X^0000 1111=1010 0001即可得到。

（2）  與0相異或，保留原值

#例如：X^0000 0000 =1010 1110

（3）兩個變數交換值

1.借助第三個變數來實現

C=A;A=B;B=C;

2.利用加減法實現兩個變數的交換

 A=A+B;B=A-B;A=A-B;

3.用位異或運算來實現，也是效率最高的

原理：一個數異或本身等於0 ；異或運算子合交換律

A=A^B;B=A ^B;A=A^B

（四）取反與運算~

對一個二進制數位取反，即將0變為1，1變0

~1=0 ;~0=1

（五）左移<<

將一個運算物件的各二進位位元全部左移若干位（左邊的二進位位丟棄，右邊補0）

例如： 2<<1 =4    10<<1=100

#若左移時捨棄的高位不包含1，則每左移一位，相當於該數乘以2。

例如：

       11(1011)<<2= 0010 1100=22

       11(0000000 ##       11(0000000 ##       11(0000000110100100100100100101010101010101001001001010122120

（六）右移>>

將一個數的各二進位位全部右移若干位，正數左補0，負數左補1，右邊丟棄。 若右移時捨高位不是1（即不是負數），操作數每右移一位，相當於該數除以2。

左補0還是補1得看被移數是正還是負。

例如：4>>2=4/2/2=1

#        -14（即1111 0010）>>2 =1111 1100=-4

#（七）無符號右移運算>>>

各位向右移指定的位數，右移後左邊空出的位元用零來填滿，移除右邊的位元被丟棄。

例如：-14>>>2

（即11111111 11111111 11111111 11110010）>> (

00

111111 11111111 11111111 11111100)=1073741820

#>>>>>&&>>gt; ;>>>>>>>>>>>>>>>>>>>>>>>>> ;>>>>>>>>>>>>>>>>>

#上述提到的負數，他的二進位表示和正數略有不同，所以在位運算的時候也與正數不同。

負數以其正數的補碼形式表示

！

以上述的-14為例，來簡單闡述原碼、反碼和補碼。

原碼

一個整數依照絕對值大小轉換成的二進制數稱為原碼

#例如：00000000 00000000 00000000 00001110 是14的原碼。

反碼

將二進位數數字取反，所得到的新二進制數稱為原二進制數的反碼。

例如：將00000000 00000000 00000000 00001110

每位取反，

注意：這兩者互為反碼

#補碼

反碼加1稱為補碼

11111111 11111111 11111111 1111

0001 +1=

11111111 11111111 111111111111111 11111111111111111011112111111101121111121111211211111211111121111121111112 #現在我們得到-14的二進位表示，現在將它左移

#-14（11111111 11111111 11111111 11110010

）<<2 =

#111110

）<<2 =#111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111112 11111111 110010

00

=？

分析：這個二進位的首位為1，表示是補碼形式，現在我們要將補碼轉換為原碼（它的正值）

跟原碼轉換為補碼相反，將補碼轉換為原碼的步驟：

#補碼減1得到反碼：（11000111）前24位為1，此處省略

---

反碼取反得到原碼（即該負數的正值）（00111000）

計算正值，正值為56

#取正值的相反數，得到結果-56

####結論：-14<<2 = -56########三、Java中進位運算######Java中二進位用的多嗎？ ######平常開發中「進位轉換」和「位元操作」用的不多，Java處理的是高層。 ######在跨平台中使用的較多，如：檔案讀寫，資料通訊。 ######來看一個場景：###############如果客戶機和伺服器都是用Java語言寫的程序，那麼當客戶機發送物件數據，我們就可以把要傳送的資料序列化serializable，伺服器端得到序列化的資料之後就可以反序列化，讀出裡面的物件資料。 ###

隨著客戶機存取量的增加，我們不考慮伺服器的效能，其實一個可行的方案就是把伺服器的Java語言改成C語言。

C語言作為底層語言，反映速度都比Java語言要快，而此時如果客戶端傳遞的還是序列化的數據，那麼伺服器端的C語言將無法解析，怎麼辦呢？我們可以把資料轉為二進位（0，1），這樣的話伺服器就可以解析這些語言。

>>>>>>>>>>>>>>>>>>>>>>> ;>>>>>>>>>>>>>>>>>>>>>>>>> ;>>>>>>>>>>>>>>

Java中基本資料類型有以下四種：

1. Int資料型態：byte（8bit，-128~127）、short（16bit）、int（32bit）、long（64bit）

2. float資料型態：單一精確度（float，32bit ）、雙精確度（double,64bit）

3. boolean類型變數的取值有true、false （都是1bit）

4. char資料類型：unicode字符，16bit

#對應的類別類型：

##Integer、 Float、Boolean、Character、Double、Short、Byte、Long

>>>>>>>>>>>>> ;>>>>>>>>>>>>>>>>>>>>>>>>> ;>>>>>>>>>>>>>>>>

（一）資料類型轉為位元組

例如：int型8143（00000000 00000000 00011111 11001111）

=>byte[] b=[-49,31,0,0]

# #第一個（低端）位元組：8143>>0*8 & 0xff=(11001111)=207（或有符號-49）

第二個（低端）位元組：8143> ;>1*8 &0xff=(00011111)=31

第三個（低階）位元組：8143>>2*8 &0xff=00000000=0

第四個（低階）位元組：8143>>3*8 &0xff=00000000=0

 

我們注意到上面的（低階）是從右往左開始的，那什麼是低端呢？我們從大小端的角度來說明。

小端法（Little-Endian）

低

位元組排放在記憶體的低位址端即該值的起始位址，高位元組排位在記憶體的高位址端##大端法（Big-Endian）

高

位元組排放在記憶體的

低位址端即該值的起始位址，低位元組排位在記憶體的高位址端 

為什麼會有大小端模式之分呢？

這是因為在電腦系統中，我們是以位元組為單位的，每個位址單元都對應一個位元組，一個位元組為8bit。但在C

語言中除了8bit的char之外，還有16bit的short型，32bit的long型（要看具體的編譯器），另外，對於位數大於8位元的處理器，例如16位元或32位元的處理器，由於暫存器寬度大於一個位元組，那麼必然存在著一個如果將多個位元組安排的問題。因此就導致了大端儲存模式和小端儲存模式。例如一個16bit的short型x，在記憶體中的位址為0x0010，x的值為0x1122，則0x11為高字節，0x22為低位元組。對於大端模式，就將0x11放在低位址中，即0x0010中，0x22放在高位址中，即0x0011中。小端模式，剛好相反。我們常用的X86結構是小端模式，而KEIL C51則為大端模式。很多的ARM，DSP都是小端模式。有些ARM處理器還可以由硬體來選擇是大端模式還是小端模式。 例如：32bit的數0x12 34 56 78（十二進位）

在Big-Endian模式CPU的存放方式（假設從位址0x4000開始存放）為

#記憶體位址

0x4000	0x4001	0x4002	0x4003
存放内容	0x78	0x56	0x34	0x12

在Little-Endian模式CPU的存放方式（假设从地址0x4000开始存放）为

内存地址	0x4000	0x4001	0x4002	0x4003
存放内容	0x12	0x34	0x56	0x78

 （二）字符串转化为字节

1.字符串->字节数组

1 String s;2 byte[] bs=s.getBytes();

2.字节数组->字符串

1 Byte[] bs=new byte[int];2 String s =new String(bs);或3 String s=new String(bs,encode);//encode指编码方式，如utf-8

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

两种类型转化为字节的方法都介绍了，下面写个小例子检验一下：

 1 public class BtyeTest { 2     /* 3      * int整型转为byte字节 4      */ 5     public static byte[] intTOBtyes(int in){ 6         byte[] arr=new byte[4]; 7         for(int i=0;i<4;i++){ 8             arr[i]=(byte)((in>>8*i) & 0xff); 9         }10         return arr;11     }12     /*13      * byte字节转为int整型14      */15     public static int bytesToInt(byte[] arr){16         int sum=0;17         for(int i=0;i<arr.length;i++){18             sum+=(int)(arr[i]&0xff)<<8*i;19         }20         return sum;21     }22     public static void main(String[] args) {23         // TODO Auto-generated method stub24         byte[] arr=intTOBtyes(8143);25         for(byte b:arr){26             System.out.print(b+" ");27         }28         System.out.println();29         System.out.println(bytesToInt(arr));30         31         //字符串与字节数组32         String str="云开的立夏de博客园";33         byte[] barr=str.getBytes();34         35         String str2=new String(barr);36         System.out.println("字符串转为字节数组：");37         for(byte b:barr){38             System.out.print(b+" ");39 40         }41         System.out.println();42 43         System.out.println("字节数组换位字符串："+str2);44         45          46     }47 48 }

运行结果：

---

结束语：最近偷懒了，没有好好学习，好几天没写文了，哎，还请大家多多监督！

以上是Java中的二進位及位元運算詳解的詳細內容。更多資訊請關注PHP中文網其他相關文章！