SPFA演算法使用教程

適用範圍：給定的圖存在負權邊，這時類似Dijkstra等演算法便沒有了用武之地，而Bellman-Ford演算法的複雜度又過高，SPFA演算法便派上用場了。 我們約定有向加權圖G不存在負權迴路，也就是最短路徑一定存在。當然，我們可以在執行演算法前做一次拓樸排序，以判斷是否有負權迴路，但這不是我們討論的重 點。

演算法思想：我們用陣列d記錄每個結點的最短路徑估計值，用鄰接表來儲存圖G。我們採取的方法是動態逼近法：設立一個先進先出的隊列用來保存待優化的結點，優化時每次取出隊首結點u，並且用u點當前的最短路徑估計值對離開u點所指向的結點v進行鬆弛操作，如果v點的最短路徑估計值有所調整，且v點不在目前的隊列中，就將v點放入隊尾。這樣不斷從佇列中取出結點來進行鬆弛操作，直到隊列空為止

# 

預期的時間複雜度O(ke) ， 其中k為所有頂點進隊的平均次數，可以證明k一般小於等於2。

 

實作方法：

　　建立一個佇列，初始時佇列裡只有起始點，再建立一個表格記錄起始點到所有點的最短路徑（該表格的初始值要賦為極大值，該點到他本身的路徑賦為0）。然後執行鬆弛操作，用佇列裡有的點作為起始點去刷新到所有點的最短路，如果刷新成功且被刷新點不在佇列中則把該點加入到佇列最後。重複執行直到佇列 為空。

判斷有無負環：
　　如果某點進入佇列的次數超過N次則存在負環（SPFA無法處理帶負環的圖）

 

 

 
 

 

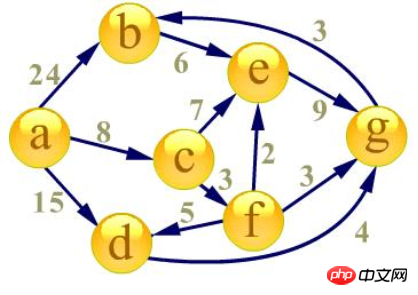
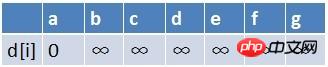
#先建立起始點a到其餘各點的
最短路徑表

                          地##  #　１、隊首元素（a）出隊，對以a為起始點的所有邊的終點依次進行鬆弛操作（此處有b,c,d三個點），此時路徑表格狀態為：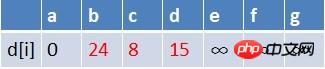

                                  

##1)1111111111011066729長度

1的這些變數都出現了最短路徑##121129的零度。點

需要入隊，此時，隊列中新入隊了三個結點b,c,d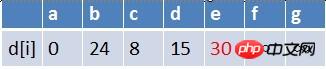

隊首元素b點出隊，以b為起始點的所有邊的終點依序進行鬆弛操作（此處只有e點），此時路徑表格狀態為：

                #在最短路徑表中，e的最短路徑估值也變小了，e在隊列中不存在，因此e也要

入隊，此時隊列中的元素為c，d，e

######隊首元素c點出隊，對以c為起始點的所有邊的終點依次進行鬆弛操作（此處有e,f兩個點），此時路徑表格狀態為：#######

                                 

##11存在因此

e不用入隊了，f要入隊，此時隊列中的元素為d，e，f

 隊首元素d點出隊，以d為起始點的所有邊的終點依序進行鬆弛操作（此處只有g這個點），此時路徑表格狀態為：

 

 

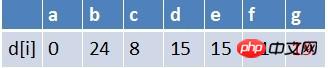                       地#1鬆弛不成功），沒有新結點入隊，隊列中元素為f，g

隊首元素f點出隊，對以f為起始點的所有邊的終點依次進行鬆弛操作（此處有d，e，g三個點），此時路徑表格狀態為：

                   

#在最短路徑表中，e，g的最短路徑估值又變小，隊列中無e點，e入隊，隊列中存在g這個點，g不用入隊，此時隊列中元素為g，e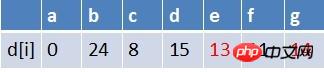
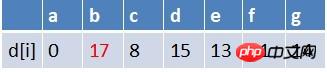
隊首元素g點出隊，對以g為起始點的所有邊的終點依次進行鬆弛操作（此處只有b點），此時路徑表格狀態為：

                           

C

C

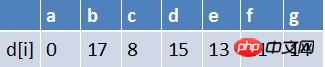
#############################都都是就是也都在最短的路徑中，最短路徑中， ，b入隊，此時隊列中元素為e，b#########隊首元素e點出隊，對以e為起始點的所有邊的終點依次進行鬆弛操作（此處只有g這個點），此時路徑表格狀態為：############ #############             #########    ”在最短路徑表中，g的最短路徑估值沒改變（鬆弛不成功），此時隊列中元素為b############隊首元素b點出隊，對以b為起始點的所有邊的終點依序進行鬆弛操作（此處只有e這個點），此時路徑表狀態為：############               ##  ####在最短路徑表中，e的最短路徑估值沒變化（鬆弛不成功），此時隊列為空了############最終a到g的最短路徑為１４######### #########java程式碼#########

package spfa负权路径;

import java.awt.List;
import java.util.ArrayList;
import java.util.Scanner;
public class SPFA {
	/**
	 * @param args
	 */
	public long[] result;         //用于得到第s个顶点到其它顶点之间的最短距离
	//数组实现邻接表存储
	class edge{
		public int a;//边的起点
		public int b;//边的终点
		public int value;//边的值
		public edge(int a,int b,int value){
			this.a=a;
			this.b=b;
			this.value=value;
		}
	}
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		SPFA spafa=new SPFA();
		Scanner scan=new Scanner(System.in);
		int n=scan.nextInt();
		int s=scan.nextInt();
		int p=scan.nextInt();
		edge[] A=new edge[p];
		for(int i=0;i<p;i++){
			int a=scan.nextInt();
			int b=scan.nextInt();
			int value=scan.nextInt();
			A[i]=spafa.new edge(a,b,value);
		}
		if(spafa.getShortestPaths(n,s,A)){
			for(int i=0;i<spafa.result.length;i++){
				System.out.println(spafa.result[i]+" ");
			}
		}else{
			System.out.println("存在负环");
		}
	}
	/*
     * 参数n:给定图的顶点个数
     * 参数s:求取第s个顶点到其它所有顶点之间的最短距离
     * 参数edge:给定图的具体边
     * 函数功能：如果给定图不含负权回路，则可以得到最终结果，如果含有负权回路，则不能得到最终结果
     */
	private boolean getShortestPaths(int n, int s, edge[] A) {
		// TODO Auto-generated method stub
		ArrayList<Integer> list = new ArrayList<Integer>();
		result=new long[n];
		boolean used[]=new boolean[n];
		int num[]=new int[n];
		for(int i=0;i<n;i++){
			result[i]=Integer.MAX_VALUE;
			used[i]=false;
		}
		result[s]=0;//第s个顶点到自身距离为0
		used[s]=true;//表示第s个顶点进入数组队
		num[s]=1;//表示第s个顶点已被遍历一次
		list.add(s); //第s个顶点入队
		while(list.size()!=0){
			int a=list.get(0);//获取数组队中第一个元素
			list.remove(0);//删除数组队中第一个元素
			for(int i=0;i<A.length;i++){
			//当list数组队的第一个元素等于边A[i]的起点时
				if(a==A[i].a&&result[A[i].b]>(result[A[i].a]+A[i].value)){
					result[A[i].b]=result[A[i].a]+A[i].value;
					if(!used[A[i].b]){
						list.add(A[i].b);
						num[A[i].b]++;
						if(num[A[i].b]>n){
							return false;
						}
						used[A[i].b]=true;//表示边A[i]的终点b已进入数组队
					}
				}
			}
			used[a]=false; //顶点a出数组对
		}
		return true;
	}
}

#########　　#################################################################################################################################################

以上是SPFA演算法使用教程的詳細內容。更多資訊請關注PHP中文網其他相關文章！