詳解Java遞歸演算法(動力節點整理)

Java遞迴演算法是基於Java語言實作的遞歸演算法。遞歸演算法對解決一大類問題很有效，它可以使演算法簡潔且易於理解。接下來透過本文介紹Java遞歸演算法相關知識，有興趣的朋友一起學習吧

遞迴演算法是一種直接或間接呼叫自身函數或方法的演算法。 Java遞歸演算法是基於Java語言實作的遞迴演算法。遞歸演算法的實質是把問題分解成規模縮小的同類問題的子問題，然後遞歸調用方法來表示問題的解。遞歸演算法對解決一大類問題很有效，它可以使演算法簡潔且易於理解。

   遞迴演算法解決問題的特性：

#    1）遞迴是方法中呼叫自己。

　 2） 在使用遞增歸策略時，必須有明確的遞迴結束條件，稱為遞迴出口。

　 3）遞歸演算法解題通常顯得很簡潔，但遞迴演算法解題的運作效率較低。所以一般不提倡用遞歸演算法設計程序。

　 4）在遞歸呼叫的過程當中系統為每一層的返回點、局部量等開闢了堆疊來儲存。遞歸次數過多容易造成棧溢位等，所以一般不提倡用遞迴演算法設計程式。

　遞迴演算法所體現的「重複」一般有三個要求：

　 一是每次呼叫在尺度上都有所縮小(通常是減半);

　 二是相鄰兩次重複之間有緊密的聯繫，前一次要為後一次做準備(通常前一次的輸出就作為後一次的輸入)；

　 三是在問題的規模極小時必須用直接給出解答而不再進行遞歸調用，因而每次遞歸調用都是有條件的(以規模未達到直接解答的大小為條件)，無條件遞歸呼叫將會成為死循環而不能正常結束。

    為了瞭解遞迴演算法，現舉一個實例說明如下：

        問題說明：

#求解Fibonacci數列的第10個位置的值？ （斐波納契數列（Fibonacci Sequence），又稱黃金分割數列，指的是這樣一個數列：1、1、2、3、5、8、13、 21、…在數學上，斐波納契數列以以下以遞歸的方法定義：F0=0，F1=1，Fn=F(n-1)+F(n-2)（n>=2 ，n∈N*））

       Java程式碼清單：

package com.bjpowernode.test; 
 
 public classFab { 
 
 public static void main(String args[]){ 
 System.out.println(fab(5)); 
 } 
 private static int fab(int index){ 
 if(index==1 || index==2){ 
  return 1; 
 }else{ 
  return fab(index-1)+fab(index-2); 
 } 
 } 
 }

        程式分析：

    遞歸實現了Fibonacci數列。這個遞歸演算法的出口是在

 if(index==1 || index==2){ 
 return 1; 
 }

              這個程式碼段上，而如果程式的index符合條件就會停止進行遞歸。所以這個程式的運作流程是：

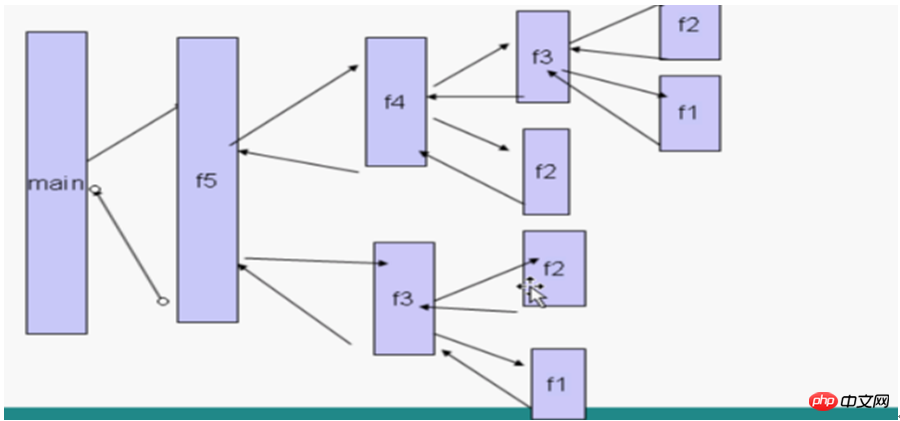
程式分析到這裡，遞迴的實作也就完成了，讀者可以自己簡單的做個demo，感受一下這個演算法的精妙之處，其實很多人都在說演算法難，難於上青天，其實掌握演算法的根才是最重要的，什麼是演算法的根呢，就拿這個遞歸演算法來說吧，我感覺這個根就是那個出口，只要找到這個出口所在，那麼演算法自然而然就能水到渠成了。

以上是詳解Java遞歸演算法(動力節點整理)的詳細內容。更多資訊請關注PHP中文網其他相關文章！