Java實現紅黑樹的深入剖析（圖）

紅黑樹是平衡二元尋找樹的一種。為了深入理解紅黑樹，我們需要從二元查找樹開始講起。

Java實現紅黑樹的深入剖析（圖）

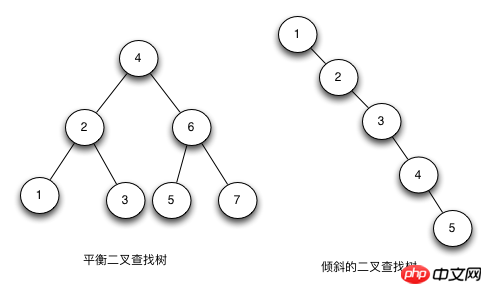
二元查找樹（Binary Search Tree，簡稱Java實現紅黑樹的深入剖析（圖））是一棵二元樹，它的左子節點的值比父節點的值小，右節點的值要比父節點的值大。它的高度決定了它的查找效率。

在理想的情況下，二元尋找樹增刪查改的時間複雜度為O(logN)（其中N為節點數），最壞的情況下為O(N)。當它的高度是logN+1時，我們就說二元查找樹是平衡的。

Java實現紅黑樹的深入剖析（圖）的查找操作

T  key = a search key
Node root = point to the root of a Java實現紅黑樹的深入剖析（圖）

while(true){
    if(root==null){
        break;
    }
    if(root.value.equals(key)){
        return root;
    }
    else if(key.compareTo(root.value)<0){
        root = root.left;
    }
    else{
        root = root.right;
    }
}
return null;

從程式中可以看出，當Java實現紅黑樹的深入剖析（圖）查找的時候，先與目前節點進行比較：

• 如果相等的話就傳回目前節點；

• 如果少於目前節點則繼續尋找目前節點的左節點；

• #如果大於目前節點則繼續尋找目前節點的右節點。

直到目前節點指標為空或查找到對應的節點，程式查找結束。

Java實現紅黑樹的深入剖析（圖）的插入操作

Node node = create a new node with specify value
Node root = point the root node of a Java實現紅黑樹的深入剖析（圖）
Node parent = null;

//find the parent node to append the new node
while(true){
   if(root==null)break;
   parent = root;
   if(node.value.compareTo(root.value)<=0){
      root = root.left;  
   }else{
      root = root.right;
   } 
}
if(parent!=null){
   if(node.value.compareTo(parent.value)<=0){//append to left
      parent.left = node;
   }else{//append to right
      parent.right = node;
   }
}

插入操作先透過循環查找到待插入的節點的父節點，和查找父節點的邏輯一樣，都是比大小，小的往左，大的往右。找到父節點後，對比父節點，小的就插入父節點的左節點，大就插入父節點的右節點。

Java實現紅黑樹的深入剖析（圖）的刪除操作

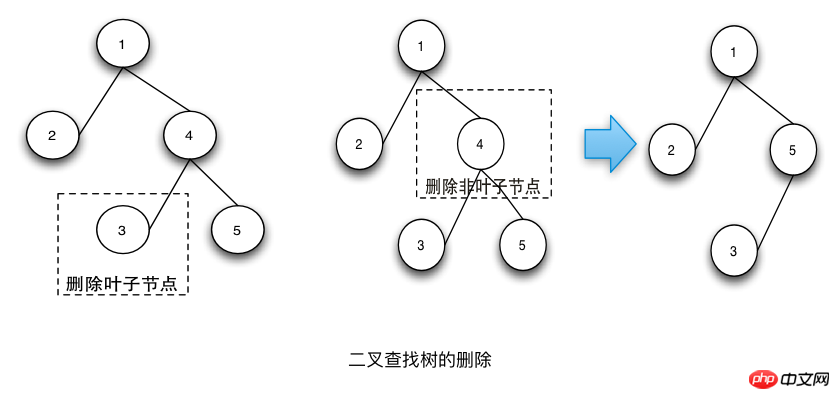
刪除操作的步驟如下：

1. #找出要刪除的節點。

2. 如果待刪除的節點是葉子節點，則直接刪除。

3. 如果待刪除的節點不是葉子節點，則先找到待刪除節點的中序遍歷的後繼節點，用該後繼節點的值替換待刪除的節點的值，然後刪除後繼節點。

Java實現紅黑樹的深入剖析（圖）存在的問題

Java實現紅黑樹的深入剖析（圖）存在的主要問題是，數在插入的時候會導致樹傾斜，不同的插入順序會導致樹的高度不一樣，而樹的高度直接的影響了樹的尋找效率。理想的高度是logN，最糟的情況是所有的節點都在一條斜線上，這樣的樹的高度是N。

RBTree

基於Java實現紅黑樹的深入剖析（圖）存在的問題，一種新的樹－平衡二元查找樹(Balanced Java實現紅黑樹的深入剖析（圖）)產生了。平衡樹在插入和刪除的時候，會透過旋轉操作將高度保持在logN。其中兩款代表性的平衡樹分別為AVL樹和紅黑樹。 AVL樹由於實作比較複雜，而且插入和刪除效能差，在實際環境下的應用不如紅黑樹。

紅黑樹（Red-Black Tree，以下簡稱RBTree）的實際應用非常廣泛，例如Linux核心中的完全公平調度器、高精度計時器、ext3檔案系統等等，各種語言的函式庫如Java的TreeMap和TreeSet，C++ STL的map、multimap、multiset等。

RBTree也是函數式語言中最常使用的持久性資料結構之一，在計算幾何中也有重要作用。值得一提的是，Java 8中HashMap的實作也因為用RBTree取代鍊錶，效能有所提升。

RBTree的定義

RBTree的定義如下:

1. 任何一個節點都有顏色，黑色或紅色

2. 根節點是黑色的

3. 父子節點之間不能出現兩個連續的紅節點

4. ##任何一個節點向下遍歷到其子孫的葉子節點，所經過的黑節點個數必須相等

5. #空節點被認為是黑色的

##資料結構表示如下：

class  Node<T>{
   public  T value;
   public   Node<T> parent;
   public   boolean isRed;
   public   Node<T> left;
   public   Node<T> right;
}

RBTree在理論上還是一棵Java實現紅黑樹的深入剖析（圖）樹，但是它在對Java實現紅黑樹的深入剖析（圖）的插入和刪除操作時會維持樹的平衡，即保證樹的高度在[logN,logN+1] （理論上，極端的情況下可以出現RBTree的高度達到2*logN，但實際上很難遇到）。這樣RBTree的查找時間複雜度始終保持在O(logN)從而接近理想的Java實現紅黑樹的深入剖析（圖）。 RBTree的刪除和插入操作的時間複雜度也是O(logN)。 RBTree的查找操作就是Java實現紅黑樹的深入剖析（圖）的查找操作。

RBTree的旋轉操作

旋轉操作(Rotate)的目的是讓節點顏色符合定義，讓RBTree的高度達到平衡。

Rotate分為left-rotate（左旋）和right-rotate（右旋），區分左旋和右旋的方法是：待旋轉的節點從左邊上升到父節點就是右旋，待旋轉的節點從右邊上升到父節點就是左旋。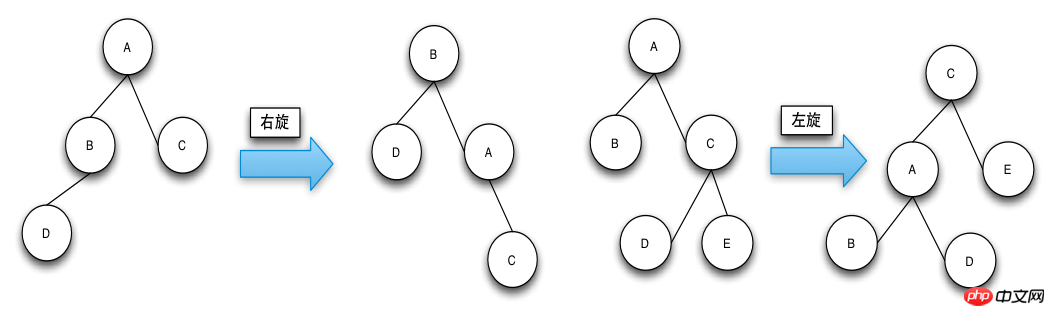

RBTree的查找操作

RBTree的查找操作和Java實現紅黑樹的深入剖析（圖）的查找操作是一樣的。請參考Java實現紅黑樹的深入剖析（圖）的查找操作代碼。

RBTree的插入操作

RBTree的插入與Java實現紅黑樹的深入剖析（圖）的插入方式是一致的，只不過是在插入過後，可能會導致樹的不平衡，這時就需要對樹進行旋轉操作和色彩修復（這裡簡稱插入修復），使得它符合RBTree的定義。

新插入的節點是紅色的，插入修復操作如果遇到父節點的顏色為黑則修復操作結束。也就是說，只有在父節點為紅色節點的時候是需要插入修復操作的。

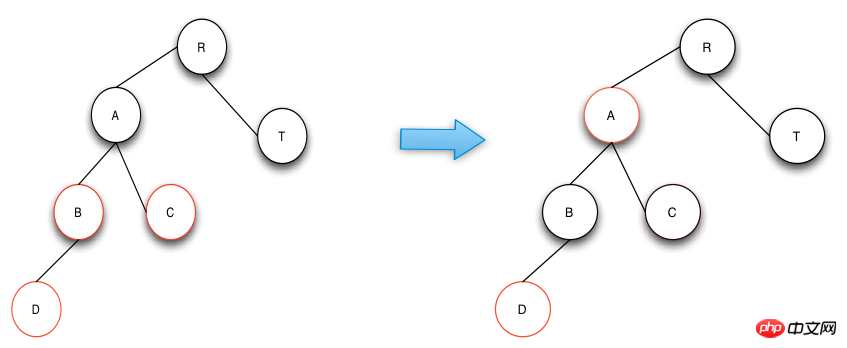
插入修復作業分為以下的三種情況，而且新插入的節點的父節點都是紅色的：

1. ##叔叔節點也是紅色。

2. 叔叔節點為空，且祖父節點、父節點和新節點處於一條斜線上。

3. 叔叔節點為空，且祖父節點、父節點和新節點不處於一條斜線上。

插入操作-case 1

case 1的操作是將父節點和叔叔節點與祖父節點的顏色互換，這樣就符合了RBTRee的定義。即維持了高度的平衡，修復後顏色也符合RBTree定義的第三條和第四條。下圖中，操作完成後A節點變成了新的節點。如果A節點的父節點不是黑色的話，則繼續做修復操作。

插入操作-case 2

case 2的操作是將B節點進行右旋操作，並且和父節點A互換顏色。透過此修復操作RBTRee的高度和顏色都符合紅黑樹的定義。如果B和C節點都是右節點的話，只要將操作變成左旋就可以了。

插入操作-case 3

case 3的操作是將C節點進行左旋，這樣就從case 3轉換成case 2了，然後針對case 2進行操作處理就行了。 case 2操作做了一個右旋操作和顏色互換來達到目的。如果樹的結構是下圖的鏡像結構，則只需要將對應的左旋變成右旋，右旋變成左旋即可。

插入操作的總結

插入後的修復操作是一個向root節點回溯的操作，一旦牽涉的節點都符合了紅黑樹的定義，修復操作結束。之所以會向上回溯是由於case 1操作會將父節點，叔叔節點和祖父節點進行換顏色，有可能會導致祖父節點不平衡(紅黑樹定義3)。這個時候需要將祖父節點為起點進行調節（向上回溯）。

祖父節點調節後如果還是遇到它的祖父顏色問題，操作就會繼續向上回溯，直到root節點為止，根據定義root節點永遠是黑色的。在向上的追溯的過程中，針對插入的3中情況進行調節。直到符合紅黑樹的定義。直到牽涉的節點都符合了紅黑樹的定義，修復作業結束。

如果上面的3中情況如果對應的操作是在右子樹上，做對應的鏡像操作就是了。

RBTree的刪除操作

刪除操作首先需要做的也是Java實現紅黑樹的深入剖析（圖）的刪除操作，刪除操作會刪除對應的節點，如果是葉子節點就直接刪除，如果是非葉子節點，會用對應的中序遍歷的後繼節點來頂替要刪除節點的位置。刪除後就需要做刪除修復操作，使的樹符合紅黑樹的定義，符合定義的紅黑樹高度是平衡的。

刪除修復操作在遇到被刪除的節點是紅色節點或到達root節點時，修復操作完畢。

刪除修復操作是針對刪除黑色節點才有的，當黑色節點被刪除後會讓整個樹不符合RBTree的定義的第四條。需要做的處理是從兄弟節點上借調黑色的節點過來，如果兄弟節點沒有黑節點可以藉調的話，就只能往上追溯，將每一級的黑節點數減去一個，使得整棵樹符合紅黑樹的定義。

刪除操作的整體思想是從兄弟節點借調黑色節點使樹保持局部的平衡，如果局部的平衡達到了，就看整體的樹是否是平衡的，如果不平衡就接著向上追溯調整。

刪除修復操作分為四種情況(刪除黑節點後)：

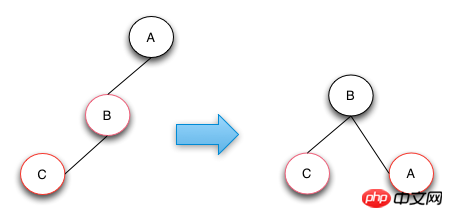
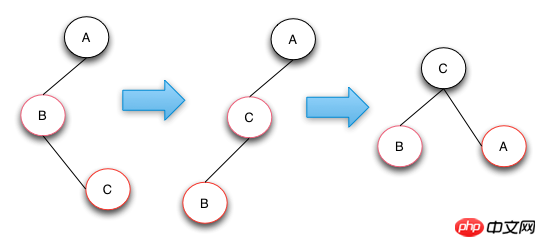
1. #待刪除的節點的兄弟節點是紅色的節點。

2. 待刪除的節點的兄弟節點是黑色的節點，且兄弟節點的子節點都是黑色的。

3. 待調整的節點的兄弟節點是黑色的節點，且兄弟節點的左子節點是紅色的，右節點是黑色的(兄弟節點在右邊)，如果兄弟節點在左邊的話，就是兄弟節點的右子節點是紅色的，左節點是黑色的。

4. 待调整的节点的兄弟节点是黑色的节点，且右子节点是是红色的(兄弟节点在右边)，如果兄弟节点在左边，则就是对应的就是左节点是红色的。

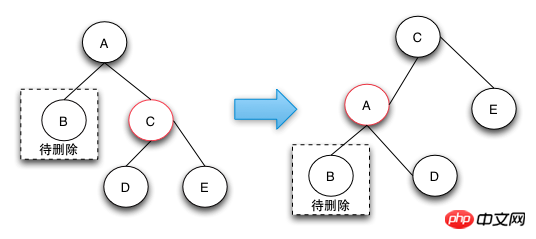
删除操作-case 1

由于兄弟节点是红色节点的时候，无法借调黑节点，所以需要将兄弟节点提升到父节点，由于兄弟节点是红色的，根据RBTree的定义，兄弟节点的子节点是黑色的，就可以从它的子节点借调了。

case 1这样转换之后就会变成后面的case 2，case 3，或者case 4进行处理了。上升操作需要对C做一个左旋操作，如果是镜像结构的树只需要做对应的右旋操作即可。

之所以要做case 1操作是因为兄弟节点是红色的，无法借到一个黑节点来填补删除的黑节点。

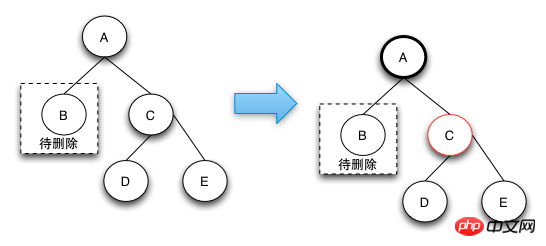
删除操作-case 2

case 2的删除操作是由于兄弟节点可以消除一个黑色节点，因为兄弟节点和兄弟节点的子节点都是黑色的，所以可以将兄弟节点变红，这样就可以保证树的局部的颜色符合定义了。这个时候需要将父节点A变成新的节点，继续向上调整，直到整颗树的颜色符合RBTree的定义为止。

case 2这种情况下之所以要将兄弟节点变红，是因为如果把兄弟节点借调过来，会导致兄弟的结构不符合RBTree的定义，这样的情况下只能是将兄弟节点也变成红色来达到颜色的平衡。当将兄弟节点也变红之后，达到了局部的平衡了，但是对于祖父节点来说是不符合定义4的。这样就需要回溯到父节点，接着进行修复操作。

删除操作-case 3

case 3的删除操作是一个中间步骤，它的目的是将左边的红色节点借调过来，这样就可以转换成case 4状态了，在case 4状态下可以将D，E节点都阶段过来，通过将两个节点变成黑色来保证红黑树的整体平衡。

之所以说case-3是一个中间状态，是因为根据红黑树的定义来说，下图并不是平衡的，他是通过case 2操作完后向上回溯出现的状态。之所以会出现case 3和后面的case 4的情况，是因为可以通过借用侄子节点的红色，变成黑色来符合红黑树定义4.

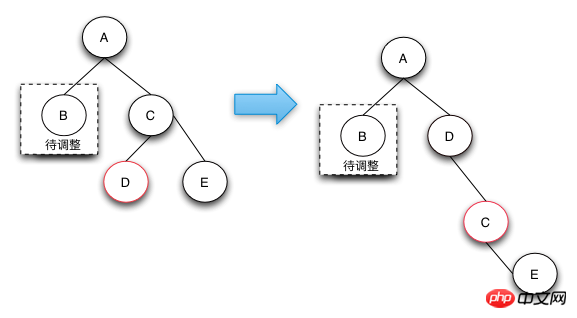
删除操作-case 4

Case 4的操作是真正的节点借调操作，通过将兄弟节点以及兄弟节点的右节点借调过来，并将兄弟节点的右子节点变成红色来达到借调两个黑节点的目的，这样的话，整棵树还是符合RBTree的定义的。

Case 4这种情况的发生只有在待删除的节点的兄弟节点为黑，且子节点不全部为黑，才有可能借调到两个节点来做黑节点使用，从而保持整棵树都符合红黑树的定义。

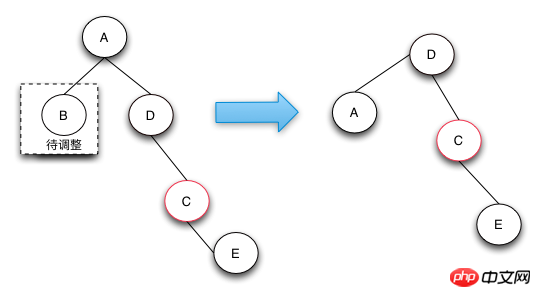
删除操作的总结

红黑树的删除操作是最复杂的操作，复杂的地方就在于当删除了黑色节点的时候，如何从兄弟节点去借调节点，以保证树的颜色符合定义。由于红色的兄弟节点是没法借调出黑节点的，这样只能通过选择操作让他上升到父节点，而由于它是红节点，所以它的子节点就是黑的，可以借调。

对于兄弟节点是黑色节点的可以分成3种情况来处理，当所以的兄弟节点的子节点都是黑色节点时，可以直接将兄弟节点变红，这样局部的红黑树颜色是符合定义的。但是整颗树不一定是符合红黑树定义的，需要往上追溯继续调整。

对于兄弟节点的子节点为左红右黑或者 (全部为红，右红左黑)这两种情况，可以先将前面的情况通过选择转换为后一种情况，在后一种情况下，因为兄弟节点为黑，兄弟节点的右节点为红，可以借调出两个节点出来做黑节点，这样就可以保证删除了黑节点，整棵树还是符合红黑树的定义的，因为黑色节点的个数没有改变。

红黑树的删除操作是遇到删除的节点为红色，或者追溯调整到了root节点，这时删除的修复操作完毕。

RBTree的Java实现

public class RBTreeNode<T extends Comparable<T>> {
    private T value;//node value
    private RBTreeNode<T> left;//left child pointer
    private RBTreeNode<T> right;//right child pointer
    private RBTreeNode<T> parent;//parent pointer
    private boolean red;//color is red or not red

    public RBTreeNode(){}
    public RBTreeNode(T value){this.value=value;}
    public RBTreeNode(T value,boolean isRed){this.value=value;this.red = isRed;}

    public T getValue() {
        return value;
    }
    void setValue(T value) {
        this.value = value;
    }
    RBTreeNode<T> getLeft() {
        return left;
    }
    void setLeft(RBTreeNode<T> left) {
        this.left = left;
    }
    RBTreeNode<T> getRight() {
        return right;
    }
    void setRight(RBTreeNode<T> right) {
        this.right = right;
    }
    RBTreeNode<T> getParent() {
        return parent;
    }
    void setParent(RBTreeNode<T> parent) {
        this.parent = parent;
    }
    boolean isRed() {
        return red;
    }
    boolean isBlack(){
        return !red;
    }
    /**
    * is leaf node
    **/
    boolean isLeaf(){
        return left==null && right==null;
    }

    void setRed(boolean red) {
        this.red = red;
    }

    void makeRed(){
        red=true;
    }
    void makeBlack(){
        red=false;
    }
    @Override
    public String toString(){
        return value.toString();
    }
}

public class RBTree<T extends Comparable<T>> {
    private final RBTreeNode<T> root;
    //node number
    private java.util.concurrent.atomic.AtomicLong size = 
                    new java.util.concurrent.atomic.AtomicLong(0);

    //in overwrite mode,all node&#39;s value can not  has same    value
    //in non-overwrite mode,node can have same value, suggest don&#39;t use non-overwrite mode.
    private volatile boolean overrideMode=true;

    public RBTree(){
        this.root = new RBTreeNode<T>();
    }

    public RBTree(boolean overrideMode){
        this();
        this.overrideMode=overrideMode;
    }

    public boolean isOverrideMode() {
        return overrideMode;
    }

    public void setOverrideMode(boolean overrideMode) {
        this.overrideMode = overrideMode;
    }

    /**
     * number of tree number
     * @return
     */
    public long getSize() {
        return size.get();
    }
    /**
     * get the root node
     * @return
     */
    private RBTreeNode<T> getRoot(){
        return root.getLeft();
    }

    /**
     * add value to a new node,if this value exist in this tree,
     * if value exist,it will return the exist value.otherwise return null
     * if override mode is true,if value exist in the tree,
     * it will override the old value in the tree
     * 
     * @param value
     * @return
     */
    public T addNode(T value){
        RBTreeNode<T> t = new RBTreeNode<T>(value);
        return addNode(t);
    }
    /**
     * find the value by give value(include key,key used for search,
     * other field is not used,@see compare method).if this value not exist return null
     * @param value
     * @return
     */
    public T find(T value){
        RBTreeNode<T> dataRoot = getRoot();
        while(dataRoot!=null){
            int cmp = dataRoot.getValue().compareTo(value);
            if(cmp<0){
                dataRoot = dataRoot.getRight();
            }else if(cmp>0){
                dataRoot = dataRoot.getLeft();
            }else{
                return dataRoot.getValue();
            }
        }
        return null;
    }
    /**
     * remove the node by give value,if this value not exists in tree return null
     * @param value include search key
     * @return the value contain in the removed node
     */
    public T remove(T value){
        RBTreeNode<T> dataRoot = getRoot();
        RBTreeNode<T> parent = root;

        while(dataRoot!=null){
            int cmp = dataRoot.getValue().compareTo(value);
            if(cmp<0){
                parent = dataRoot;
                dataRoot = dataRoot.getRight();
            }else if(cmp>0){
                parent = dataRoot;
                dataRoot = dataRoot.getLeft();
            }else{
                if(dataRoot.getRight()!=null){
                    RBTreeNode<T> min = removeMin(dataRoot.getRight());
                    //x used for fix color balance
                    RBTreeNode<T> x = min.getRight()==null ? min.getParent() : min.getRight();
                    boolean isParent = min.getRight()==null;

                    min.setLeft(dataRoot.getLeft());
                    setParent(dataRoot.getLeft(),min);
                    if(parent.getLeft()==dataRoot){
                        parent.setLeft(min);
                    }else{
                        parent.setRight(min);
                    }
                    setParent(min,parent);

                    boolean curMinIsBlack = min.isBlack();
                    //inherit dataRoot&#39;s color
                    min.setRed(dataRoot.isRed());

                    if(min!=dataRoot.getRight()){
                        min.setRight(dataRoot.getRight());
                        setParent(dataRoot.getRight(),min);
                    }
                    //remove a black node,need fix color
                    if(curMinIsBlack){
                        if(min!=dataRoot.getRight()){
                            fixRemove(x,isParent);
                        }else if(min.getRight()!=null){
                            fixRemove(min.getRight(),false);
                        }else{
                            fixRemove(min,true);
                        }
                    }
                }else{
                    setParent(dataRoot.getLeft(),parent);
                    if(parent.getLeft()==dataRoot){
                        parent.setLeft(dataRoot.getLeft());
                    }else{
                        parent.setRight(dataRoot.getLeft());
                    }
                    //current node is black and tree is not empty
                    if(dataRoot.isBlack() && !(root.getLeft()==null)){
                        RBTreeNode<T> x = dataRoot.getLeft()==null 
                                            ? parent :dataRoot.getLeft();
                        boolean isParent = dataRoot.getLeft()==null;
                        fixRemove(x,isParent);
                    }
                }
                setParent(dataRoot,null);
                dataRoot.setLeft(null);
                dataRoot.setRight(null);
                if(getRoot()!=null){
                    getRoot().setRed(false);
                    getRoot().setParent(null);
                }
                size.decrementAndGet();
                return dataRoot.getValue();
            }
        }
        return null;
    }
    /**
     * fix remove action
     * @param node
     * @param isParent
     */
    private void fixRemove(RBTreeNode<T> node,boolean isParent){
        RBTreeNode<T> cur = isParent ? null : node;
        boolean isRed = isParent ? false : node.isRed();
        RBTreeNode<T> parent = isParent ? node : node.getParent();

        while(!isRed && !isRoot(cur)){
            RBTreeNode<T> sibling = getSibling(cur,parent);
            //sibling is not null,due to before remove tree color is balance

            //if cur is a left node
            boolean isLeft = parent.getRight()==sibling;
            if(sibling.isRed() && !isLeft){//case 1
                //cur in right
                parent.makeRed();
                sibling.makeBlack();
                rotateRight(parent);
            }else if(sibling.isRed() && isLeft){
                //cur in left
                parent.makeRed();
                sibling.makeBlack();
                rotateLeft(parent);
            }else if(isBlack(sibling.getLeft()) && isBlack(sibling.getRight())){//case 2
                sibling.makeRed();
                cur = parent;
                isRed = cur.isRed();
                parent=parent.getParent();
            }else if(isLeft && !isBlack(sibling.getLeft()) 
                                    && isBlack(sibling.getRight())){//case 3
                sibling.makeRed();
                sibling.getLeft().makeBlack();
                rotateRight(sibling);
            }else if(!isLeft && !isBlack(sibling.getRight()) 
                                            && isBlack(sibling.getLeft()) ){
                sibling.makeRed();
                sibling.getRight().makeBlack();
                rotateLeft(sibling);
            }else if(isLeft && !isBlack(sibling.getRight())){//case 4
                sibling.setRed(parent.isRed());
                parent.makeBlack();
                sibling.getRight().makeBlack();
                rotateLeft(parent);
                cur=getRoot();
            }else if(!isLeft && !isBlack(sibling.getLeft())){
                sibling.setRed(parent.isRed());
                parent.makeBlack();
                sibling.getLeft().makeBlack();
                rotateRight(parent);
                cur=getRoot();
            }
        }
        if(isRed){
            cur.makeBlack();
        }
        if(getRoot()!=null){
            getRoot().setRed(false);
            getRoot().setParent(null);
        }

    }
    //get sibling node
    private RBTreeNode<T> getSibling(RBTreeNode<T> node,RBTreeNode<T> parent){
        parent = node==null ? parent : node.getParent();
        if(node==null){
            return parent.getLeft()==null ? parent.getRight() : parent.getLeft();
        }
        if(node==parent.getLeft()){
            return parent.getRight();
        }else{
            return parent.getLeft();
        }
    }

    private boolean isBlack(RBTreeNode<T> node){
        return node==null || node.isBlack();
    }
    private boolean isRoot(RBTreeNode<T> node){
        return root.getLeft() == node && node.getParent()==null;
    }
    /**
     * find the successor node
     * @param node current node&#39;s right node
     * @return
     */
    private RBTreeNode<T> removeMin(RBTreeNode<T> node){
        //find the min node
        RBTreeNode<T> parent = node;
        while(node!=null && node.getLeft()!=null){
            parent = node;
            node = node.getLeft();
        }
        //remove min node
        if(parent==node){
            return node;
        }

        parent.setLeft(node.getRight());
        setParent(node.getRight(),parent);

        //don&#39;t remove right pointer,it is used for fixed color balance
        //node.setRight(null);
        return node;
    }

    private T addNode(RBTreeNode<T> node){
        node.setLeft(null);
        node.setRight(null);
        node.setRed(true);
        setParent(node,null);
        if(root.getLeft()==null){
            root.setLeft(node);
            //root node is black
            node.setRed(false);
            size.incrementAndGet();
        }else{
            RBTreeNode<T> x = findParentNode(node);
            int cmp = x.getValue().compareTo(node.getValue());

            if(this.overrideMode && cmp==0){
                T v = x.getValue();
                x.setValue(node.getValue());
                return v;
            }else if(cmp==0){
                //value exists,ignore this node
                return x.getValue();
            }

            setParent(node,x);

            if(cmp>0){
                x.setLeft(node);
            }else{
                x.setRight(node);
            }

            fixInsert(node);
            size.incrementAndGet();
        }
        return null;
    }

    /**
     * find the parent node to hold node x,if parent value equals x.value return parent.
     * @param x
     * @return
     */
    private RBTreeNode<T> findParentNode(RBTreeNode<T> x){
        RBTreeNode<T> dataRoot = getRoot();
        RBTreeNode<T> child = dataRoot;

        while(child!=null){
            int cmp = child.getValue().compareTo(x.getValue());
            if(cmp==0){
                return child;
            }
            if(cmp>0){
                dataRoot = child;
                child = child.getLeft();
            }else if(cmp<0){
                dataRoot = child;
                child = child.getRight();
            }
        }
        return dataRoot;
    }

    /**
     * red black tree insert fix.
     * @param x
     */
    private void fixInsert(RBTreeNode<T> x){
        RBTreeNode<T> parent = x.getParent();

        while(parent!=null && parent.isRed()){
            RBTreeNode<T> uncle = getUncle(x);
            if(uncle==null){//need to rotate
                RBTreeNode<T> ancestor = parent.getParent();
                //ancestor is not null due to before before add,tree color is balance
                if(parent == ancestor.getLeft()){
                    boolean isRight = x == parent.getRight();
                    if(isRight){
                        rotateLeft(parent);
                    }
                    rotateRight(ancestor);

                    if(isRight){
                        x.setRed(false);
                        parent=null;//end loop
                    }else{
                        parent.setRed(false);
                    }
                    ancestor.setRed(true);
                }else{
                    boolean isLeft = x == parent.getLeft();
                    if(isLeft){
                        rotateRight(parent);
                    }
                    rotateLeft(ancestor);

                    if(isLeft){
                        x.setRed(false);
                        parent=null;//end loop
                    }else{
                        parent.setRed(false);
                    }
                    ancestor.setRed(true);
                }
            }else{//uncle is red
                parent.setRed(false);
                uncle.setRed(false);
                parent.getParent().setRed(true);
                x=parent.getParent();
                parent = x.getParent();
            }
        }
        getRoot().makeBlack();
        getRoot().setParent(null);
    }
    /**
     * get uncle node
     * @param node
     * @return
     */
    private RBTreeNode<T> getUncle(RBTreeNode<T> node){
        RBTreeNode<T> parent = node.getParent();
        RBTreeNode<T> ancestor = parent.getParent();
        if(ancestor==null){
            return null;
        }
        if(parent == ancestor.getLeft()){
            return ancestor.getRight();
        }else{
            return ancestor.getLeft();
        }
    }

    private void rotateLeft(RBTreeNode<T> node){
        RBTreeNode<T> right = node.getRight();
        if(right==null){
            throw new java.lang.IllegalStateException("right node is null");
        }
        RBTreeNode<T> parent = node.getParent();
        node.setRight(right.getLeft());
        setParent(right.getLeft(),node);

        right.setLeft(node);
        setParent(node,right);

        if(parent==null){//node pointer to root
            //right  raise to root node
            root.setLeft(right);
            setParent(right,null);
        }else{
            if(parent.getLeft()==node){
                parent.setLeft(right);
            }else{
                parent.setRight(right);
            }
            //right.setParent(parent);
            setParent(right,parent);
        }
    }

    private void rotateRight(RBTreeNode<T> node){
        RBTreeNode<T> left = node.getLeft();
        if(left==null){
            throw new java.lang.IllegalStateException("left node is null");
        }
        RBTreeNode<T> parent = node.getParent();
        node.setLeft(left.getRight());
        setParent(left.getRight(),node);

        left.setRight(node);
        setParent(node,left);

        if(parent==null){
            root.setLeft(left);
            setParent(left,null);
        }else{
            if(parent.getLeft()==node){
                parent.setLeft(left);
            }else{
                parent.setRight(left);
            }
            setParent(left,parent);
        }
    }

    private void setParent(RBTreeNode<T> node,RBTreeNode<T> parent){
        if(node!=null){
            node.setParent(parent);
            if(parent==root){
                node.setParent(null);
            }
        }
    }
    /**
     * debug method,it used print the given node and its children nodes,
     * every layer output in one line
     * @param root
     */
    public void printTree(RBTreeNode<T> root){
        java.util.LinkedList<RBTreeNode<T>> queue =new java.util.LinkedList<RBTreeNode<T>>();
        java.util.LinkedList<RBTreeNode<T>> queue2 =new java.util.LinkedList<RBTreeNode<T>>();
        if(root==null){
            return ;
        }
        queue.add(root);
        boolean firstQueue = true;

        while(!queue.isEmpty() || !queue2.isEmpty()){
            java.util.LinkedList<RBTreeNode<T>> q = firstQueue ? queue : queue2;
            RBTreeNode<T> n = q.poll();

            if(n!=null){
                String pos = n.getParent()==null ? "" : ( n == n.getParent().getLeft() 
                                                                        
                ? " LE" : " RI");
                String pstr = n.getParent()==null ? "" : n.getParent().toString();
                String cstr = n.isRed()?"R":"B";
                cstr = n.getParent()==null ? cstr : cstr+" ";
                System.out.print(n+"("+(cstr)+pstr+(pos)+")"+"\t");
                if(n.getLeft()!=null){
                    (firstQueue ? queue2 : queue).add(n.getLeft());
                }
                if(n.getRight()!=null){
                    (firstQueue ? queue2 : queue).add(n.getRight());
                }
            }else{
                System.out.println();
                firstQueue = !firstQueue;
            }
        }
    }

    public static void main(String[] args) {
        RBTree<String> bst = new RBTree<String>();
        bst.addNode("d");
        bst.addNode("d");
        bst.addNode("c");
        bst.addNode("c");
        bst.addNode("b");
        bst.addNode("f");

        bst.addNode("a");
        bst.addNode("e");

        bst.addNode("g");
        bst.addNode("h");

        bst.remove("c");

        bst.printTree(bst.getRoot());
    }
}

代码调试的时候，printTree输出格式如下:

d(B)
b(B d LE) g(R d RI)
a(R b LE) e(B g LE) h(B g RI)
f(R e RI)

括号左边表示元素的内容。括号内的第一个元素表示颜色，B表示black，R表示red；第二个元素表示父元素的值；第三个元素表示左右，LE表示在父元素的左边。RI表示在父元素的右边。

第一个元素d是root节点，由于它没有父节点，所以括号内只有一个元素。

总结

作为平衡二叉查找树里面众多的实现之一，红黑树无疑是最简洁、实现最为简单的。红黑树通过引入颜色的概念，通过颜色这个约束条件的使用来保持树的高度平衡。作为平衡二叉查找树，旋转是一个必不可少的操作。通过旋转可以降低树的高度，在红黑树里面还可以转换颜色。

红黑树里面的插入和删除的操作比较难理解，这时要注意记住一点：操作之前红黑树是平衡的，颜色是符合定义的。在操作的时候就需要向兄弟节点、父节点、侄子节点借调和互换颜色，要达到这个目的，就需要不断的进行旋转。所以红黑树的插入删除操作需要不停的旋转，一旦借调了别的节点，删除和插入的节点就会达到局部的平衡（局部符合红黑树的定义），但是被借调的节点就不会平衡了，这时就需要以被借调的节点为起点继续进行调整，直到整棵树都是平衡的。在整个修复的过程中，插入具体的分为3种情况，删除分为4种情况。

整个红黑树的查找，插入和删除都是O(logN)的，原因就是整个红黑树的高度是logN，查找从根到叶，走过的路径是树的高度，删除和插入操作是从叶到根的，所以经过的路径都是logN。

以上是Java實現紅黑樹的深入剖析（圖）的詳細內容。更多資訊請關注PHP中文網其他相關文章！