python 排序演算法總結及實例
- 高洛峰原創
- 2017-02-24 15:19:321905瀏覽
這篇文章主要介紹了python 排序演算法總結及實例詳解的相關資料,需要的朋友可以參考下
總結了一下常見集中排序的演算法
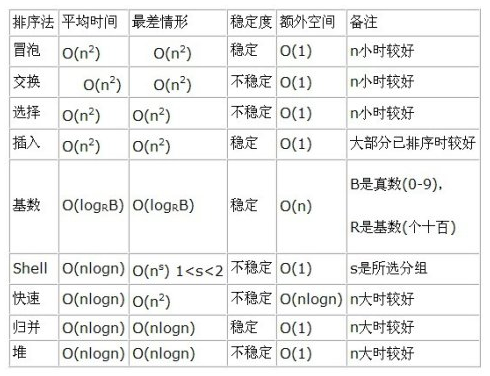
歸併排序
歸併排序也稱為合併排序,是分治法的典型應用。分治思想是將每個問題分解成個小問題,將每個小問題解決,然後合併。
具體的歸併排序就是,將一組無序數依n/2遞歸分解成只有一個元素的子項,一個元素就是已經排好序的了。然後將這些有序的子元素進行合併。
合併的過程就是對兩個已經排好序的子序列,先選取兩個子序列中最小的元素進行比較,選取兩個元素中最小的那個子序列並將其從子序列中
去掉加入到最終的結果集中,直到兩個子序列歸併完成。
程式碼如下:
#!/usr/bin/python
import sys
def merge(nums, first, middle, last):
''''' merge '''
# 切片边界,左闭右开并且是了0为开始
lnums = nums[first:middle+1]
rnums = nums[middle+1:last+1]
lnums.append(sys.maxint)
rnums.append(sys.maxint)
l = 0
r = 0
for i in range(first, last+1):
if lnums[l] < rnums[r]:
nums[i] = lnums[l]
l+=1
else:
nums[i] = rnums[r]
r+=1
def merge_sort(nums, first, last):
''''' merge sort
merge_sort函数中传递的是下标,不是元素个数
'''
if first < last:
middle = (first + last)/2
merge_sort(nums, first, middle)
merge_sort(nums, middle+1, last)
merge(nums, first, middle,last)
if __name__ == '__main__':
nums = [10,8,4,-1,2,6,7,3]
print 'nums is:', nums
merge_sort(nums, 0, 7)
print 'merge sort:', nums
穩定,時間複雜度O(nlog n)
#插入排序
程式碼如下:
#!/usr/bin/python
importsys
definsert_sort(a):
''''' 插入排序
有一个已经有序的数据序列,要求在这个已经排好的数据序列中插入一个数,
但要求插入后此数据序列仍然有序。刚开始 一个元素显然有序,然后插入一
个元素到适当位置,然后再插入第三个元素,依次类推
'''
a_len = len(a)
if a_len = 0 and a[j] > key:
a[j+1] = a[j]
j-=1
a[j+1] = key
return a
if __name__ == '__main__':
nums = [10,8,4,-1,2,6,7,3]
print 'nums is:', nums
insert_sort(nums)
print 'insert sort:', nums
#穩定,時間複雜度O(n^2)
交換兩個元素的值python中你可以這麼寫:a, b = b, a,其實這是因為賦值符號的左右兩邊都是元組
(這裡需要強調的是,在python中,元組其實是由逗號「,」來界定的,而不是括號)。
選擇排序
選擇排序(Selection sort)是一種簡單直覺的排序演算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到
排序序列的起始位置,然後,再從剩餘未排序元素中繼續尋找最小(大)元素,然後放到已排序序列的末端。以此類推,直到所
有元素均排序完畢。
import sys
def select_sort(a):
''''' 选择排序
每一趟从待排序的数据元素中选出最小(或最大)的一个元素,
顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
选择排序是不稳定的排序方法。
'''
a_len=len(a)
for i in range(a_len):#在0-n-1上依次选择相应大小的元素
min_index = i#记录最小元素的下标
for j in range(i+1, a_len):#查找最小值
if(a[j]<a[min_index]):
min_index=j
if min_index != i:#找到最小元素进行交换
a[i],a[min_index] = a[min_index],a[i]
if __name__ == '__main__':
A = [10, -3, 5, 7, 1, 3, 7]
print 'Before sort:',A
select_sort(A)
print 'After sort:',A
不穩定,時間複雜度O(n^2)
Wol排序
#希爾排序,也稱遞減增量排序演算法,希爾排序為非穩定排序演算法。此方法又稱縮小增量排序,因DL. Shell於1959年提出而得名。
先取一個小於n的整數d1作為第一個增量,把檔案的全部記錄分成d1個群組。所有距離為d1的倍數的記錄放在同一個組別中。先在各組內排序;
然後,取第二個增量d2
import sys
def shell_sort(a):
''''' shell排序
'''
a_len=len(a)
gap=a_len/2#增量
while gap>0:
for i in range(a_len):#对同一个组进行选择排序
m=i
j=i+1
while j<a_len:
if a[j]<a[m]:
m=j
j+=gap#j增加gap
if m!=i:
a[m],a[i]=a[i],a[m]
gap/=2
if __name__ == '__main__':
A = [10, -3, 5, 7, 1, 3, 7]
print 'Before sort:',A
shell_sort(A)
print 'After sort:',A
不穩定,時間複雜度平均時間O(nlogn) 最差時間O(n^s)1
堆排序( Heap Sort )
「堆」的定義:在起始索引為0 的「堆」:
節點i 的右子節點在位置2 * i + 24) 節點i 的父節點在位置floor( (i – 1) / 2 ) : 註floor 表示「取整」操作
堆的特性:
每個節點的鍵值一定總是大於(或小於)它的父節點
「最大堆」:
「堆」的根節點保存的是鍵值最大的節點。即「堆」中每個節點的鍵值總是大於它的子節點。
上移,下移:
當某節點的鍵值大於它的父節點時,這時我們就要進行「上移」操作,也就是我們把該節點移到它的父節點的位置,而讓它的父節點到它的位置上,然後我們繼續判斷該節點,直到節點不再大於它的父節點為止才停止「上移」。
現在我們再來了解「下移」操作。當我們把某節點的鍵值改小了之後,我們就要對其進行「下移」操作。
方法:
我們先建立一個最大堆(時間複雜度O(n)),然後每次我們只需要把根節點與最後一個位置的節點交換,然後把最後一個位置排除之外,然後把交換後根節點的堆進行調整(時間複雜度O(lgn) ),也就是對根節點進行「下移」操作即可。 堆排序的總的時間複雜度為O(nlgn).
程式碼如下:
#!/usr/bin env python
# 数组编号从 0开始
def left(i):
return 2*i +1
def right(i):
return 2*i+2
#保持最大堆性质 使以i为根的子树成为最大堆
def max_heapify(A, i, heap_size):
if heap_size <= 0:
return
l = left(i)
r = right(i)
largest = i # 选出子节点中较大的节点
if l A[largest]:
largest = l
if r A[largest]:
largest = r
if i != largest :#说明当前节点不是最大的,下移
A[i], A[largest] = A[largest], A[i] #交换
max_heapify(A, largest, heap_size)#继续追踪下移的点
#print A
# 建堆
def bulid_max_heap(A):
heap_size = len(A)
if heap_size >1:
node = heap_size/2 -1
while node >= 0:
max_heapify(A, node, heap_size)
node -=1
# 堆排序 下标从0开始
def heap_sort(A):
bulid_max_heap(A)
heap_size = len(A)
i = heap_size - 1
while i > 0 :
A[0],A[i] = A[i], A[0] # 堆中的最大值存入数组适当的位置,并且进行交换
heap_size -=1 # heap 大小 递减 1
i -= 1 # 存放堆中最大值的下标递减 1
max_heapify(A, 0, heap_size)
if __name__ == '__main__' :
A = [10, -3, 5, 7, 1, 3, 7]
print 'Before sort:',A
heap_sort(A)
print 'After sort:',A##不穩定,時間複雜度O( nlog n)
快速排序
#!/usr/bin/env python
# 快速排序
'''''
划分 使满足 以A[r]为基准对数组进行一个划分,比A[r]小的放在左边,
比A[r]大的放在右边
快速排序的分治partition过程有两种方法,
一种是上面所述的两个指针索引一前一后逐步向后扫描的方法,
另一种方法是两个指针从首位向中间扫描的方法。
'''
#p,r 是数组A的下标
def partition1(A, p ,r):
'''''
方法一,两个指针索引一前一后逐步向后扫描的方法
'''
x = A[r]
i = p-1
j = p
while j < r:
if A[j] < x:
i +=1
A[i], A[j] = A[j], A[i]
j += 1
A[i+1], A[r] = A[r], A[i+1]
return i+1
def partition2(A, p, r):
'''''
两个指针从首尾向中间扫描的方法
'''
i = p
j = r
x = A[p]
while i = x and i < j:
j -=1
A[i] = A[j]
while A[i]<=x and i < j:
i +=1
A[j] = A[i]
A[i] = x
return i
# quick sort
def quick_sort(A, p, r):
'''''
快速排序的最差时间复杂度为O(n2),平时时间复杂度为O(nlgn)
'''
if p < r:
q = partition2(A, p, r)
quick_sort(A, p, q-1)
quick_sort(A, q+1, r)
if __name__ == '__main__':
A = [5,-4,6,3,7,11,1,2]
print 'Before sort:',A
quick_sort(A, 0, 7)
print 'After sort:',A
不穩定,時間複雜度最理想O(nlogn)最差時間O(n^2)
說下python中的序列:
列表、元組和字串都是序列,但是序列是什麼,為什麼它們如此特別呢?序列的兩個主要特點是索引操作符和切片操作符。索引操作符讓我們可以從序列中抓取一個特定項目。切片運算子讓我們能夠取得序列的一個切片,即一部分序列,如:a = ['aa','bb','cc'], print a[0] 為索引操作,print a[0:2]為切片操作。
希望透過此文掌握Python 演算法排序的知識,謝謝大家對本站的支持!
更多python 排序演算法總結及實例相關文章請關注PHP中文網!

