從無限極分類記憶體佔用看“遞歸”

在PHP的無限級分類中，用到的很多方法都是遞歸，但是我們對遞歸的理解還很模糊，我們接下來就深入理解下遞歸的優缺點，讓大家能有個全面的認識。

什麼是遞迴？

定義

遞歸（英文：Recursion），又譯為遞回，在數學與電腦科學中，是指在函數的定義中使用函數本身的方法。

英文的Recursion從字源分析只是"re-  (again)" + "curs- （come, happen）" 也就是重複發生，再次重現的意思。 而對應的中文翻譯 」遞歸「 卻表達了兩個意思：」遞「＋」歸「。 這兩個意思，正是遞迴思想的精華所在。從這層次來看，中文翻譯反而更達意。

在網上看到個又去的比喻：

假設你在一個電影院，你想知道自己坐在哪一排，但是前面人很多，你懶得去數了，於是你問前一排的人「你坐在哪一排？」，這樣前面的人(代號A) 回答你以後，你就知道自己在哪一排了——只要把A 的答案加一，就是自己所在的排了。不料 A 比你還懶，他也不想數，於是他也問他前面的人 B「你坐在哪一排？」，這樣 A 可以用和你一模一樣的步驟知道自己所在的排。然後 B 也如法炮製。直到他們這一串人問到了最前面的一排，第一排的人告訴問問題的人「我在第一排」。最後大家就都知道自己在哪一排了。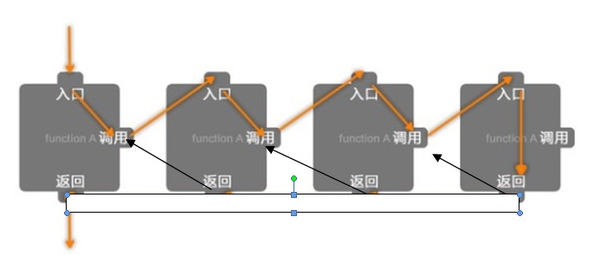

跟循環的區別

單看上面wiki的定義，貌似跟通常所說的無限死循環很像，很像他們的區別在哪？

遞歸是靜中有動，有去有回。
循環是動靜如一，有去無回。

舉個例子，給你一把鑰匙，你站在門前面，問你用這把鑰匙能打開幾扇門。

遞歸：你打開面前這扇門，看到屋裡面還有一扇門（這門可能跟前面打開的門一樣大小（靜），也可能門小了些（動）），你走過去，發現手中的鑰匙還可以打開它，你推開門，發現裡面還有一扇門，你繼續打開，。 。 。 ， 若乾次之後，你打開面前一扇門，發現只有一間房子，沒有門了。 你開始原路返回，每走回一間屋子，你數一次，走到入口的時候，你可以回答出你到底用這鑰匙開了幾扇門。

循環：你打開面前這扇門，看到屋裡面還有一扇門，（這門可能跟前面打開的門一樣大小（靜），也可能門小了些（動）），你走過去，發現手中的鑰匙還可以打開它，你推開門，發現裡面還有一扇門，（前面門如果一樣，這門也是一樣，第二扇門如果相比第一扇門變小了，這扇門也比第二扇門變小了（動靜如一，要么沒有變化，要么同樣的變化）），你繼續打開這扇門，。 。 。 ，一直這樣走下去。 入口處的人始終等不到你回去告訴他答案。

遞歸思想

遞歸就是有去（遞去）有回（歸來）。

具體來說，為什麼可以」有去「？
這要求遞歸的問題需要是可以用同樣的解題思路來回答類似但略有不同的問題（上面例子中的那一把鑰匙可以開後面門上的鎖）。

為什麼可以」有回「？
這要求這些問題不斷從大到小，從近及遠的過程中，會有一個終點，一個臨界點，一個baseline，一個你到了那個點就不用再往更小，更遠的地方走下去的點，然後從那點開始，原路回到原點。

遞歸的基本思想是把規模大的問題轉化為規模小的相似的子問題來解決。在函數實作時，因為解決大問題的方法和解決小問題的方法往往是同一個方法，所以就產生了函數呼叫它本身的情況。另外這個解決問題的函數必須有明顯的結束條件，這樣就不會產生無限遞歸的情況了。

什麼時候需要用遞歸？

當有些問題的定義本身就是遞歸形式的時候，最是適合用遞歸來解決。

電腦專業的同學最熟悉的莫過於」樹「的定義了[4,5]。還有一些定義，像是階乘，Fibonacci數列[6]，等等。用遞歸來解決這些問題，往往幾行程式碼就搞定了一些看起來相當」嚇人「的問題。 當然，遞歸的效能問題是另一回事，棧的分配，函數呼叫代價都是在具體工程實務中要考慮的。 但現在只是討論遞歸思想的話，不妨先放下那些，欣賞下遞歸的美。

---

遞歸在解決某些問題的時候使得我們思考的方式得以簡化，程式碼也更加精煉，容易閱讀。那麼既然遞歸有這麼多的優點，我們是不是什麼問題都要用遞歸來解決呢？難道遞歸就沒有缺點嗎？今天我們就來討論一下遞歸的不足之處。談到遞歸就不得不面對它的效率問題。

為什麼遞歸的效率低效率？

還是拿斐波那契（Fibonacci）數列來做範例。在許多教科書或文章中涉及到遞歸或計算複雜性的地方都會將計算斐波那契數列的程式作為經典範例。如果現在讓你以最快的速度用C#寫出一個計算斐波那契數列第n個數的函數（不考慮參數小於1或結果溢出等異常情況），我不知你的程式是否會和下列程式碼類似：

public static ulong Fib(ulong n)
{
    return (n == 1 || n == 2) ? 1 : Fib(n - 1) + Fib(n - 2);
}

這段程式碼應該算是短小精悍（執行程式碼只有一行），直觀清晰，而且非常符合許多程式設計師的程式設計美學，許多人在面試時寫出這樣的程式碼可能心裡還會暗爽。但如果用這段程式碼試試計算Fib(1000)我想就再也爽不起來了，它的運行時間也許會讓你抓狂。

看來好看的程式碼未必中用，如果程式在效率不能接受那美觀神馬的就都是浮雲了。如果簡單分析程式的執行流，就會發現問題在哪，以計算Fibonacci(5)為例：

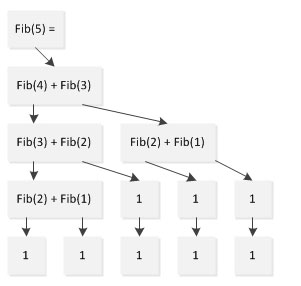
從上圖可以看出，在計算Fib(5)的過程中，Fib(1 )計算了兩次、Fib(2)計算了3次，Fib(3)計算了兩次，本來只需要5次計算就可以完成的任務卻計算了9次。這個問題隨著規模的增加會愈發凸顯，以至於Fib(1000)已經無法再可接受的時間內算出。

我們當時使用的是簡單的用定義來求 fib(n)，也就是使用公式 fib(n) = fib(n-1) + fib(n-2)。這樣的想法是很容易想到的，可是仔細分析一下我們發現，當呼叫fib(n-1)的時候，還要呼叫fib(n-2)，也就是說fib(n-2)呼叫了兩次，同樣的道理，呼叫f(n-2)時f(n-3)也呼叫了兩次，而這些冗餘的呼叫是完全沒有必要的。可以計算這個演算法的複雜度是指數級的。

改進的斐波那契遞歸演算法

那麼計算斐波那契數列是否有更好的遞歸演算法呢？ 當然有。讓我們來觀察一下斐波那契數列的前幾項：

11, 1, 2, 3, 5, 8, 13, 21, 34, 55 …

注意到沒有，如果我們去掉前面一項，得到的數列依然滿足f(n) = f(n-1) – f(n-2), (n>2)，而我們得到的數列是以1，2開頭的。很容易發現這個數列的第n-1項就是原數列的第n項。怎麼樣，知道我們該怎麼設計演算法了吧？我們可以寫這樣的一個函數，它接受三個參數，前兩個是數列的開頭兩項，第三個是我們想要求的以前兩個參數開頭的數列的第幾項。

1int fib_i(int a, int b, int n);

在函數內部我們先檢查n的值，如果n為3則我們只需返回a+b即可，這是簡單情境。如果n>3，那麼我們就呼叫f(b, a+b, n-1)，這樣我們就縮小了問題的規模（從求第n項變成求第n-1項）。好了，最終程式碼如下：

int fib_i(int a, int b , int n)
{
    if(n == 3)
        return a+b;
    else
        return fib_i(b, a+b, n-1);
}

為什麼對記憶體有很大的開銷？

遞歸的原理是：先將要計算的變數值存到堆疊中，依序循環，直到遞歸結束條件滿足時，才從堆疊中取出要計算的變數值，計算得到最終結果。
打個比喻：要計算   10！ =
遞歸的話，過程：10！ =10 * 9!
               9!=9 * 8!
           2！ =2 *1！
                 1！ =1
計算時，它是將一個一個表達式存到內存，直到遞歸條件滿足1！ =1，這樣再從記憶體中取出剛才存的表達式，得到最終的結果。這樣的話，會花銷更大的系統資源。

而且系統會設定最大遞歸深度。大於該深度時，就報錯退出。函數遞歸呼叫過程中，函數中的參數，傳回值等會不停的壓棧。函數呼叫會不停地使用棧，報存現場，恢復現場，所以記憶體開銷會越來越大，解決的方法是為尾遞歸，但是，PHP對尾遞歸沒有最佳化效果，所以這個解決方案沒有什麼實際意義。