java程式設計面試過程中常見的10大演算法概念總表

以下是在程式設計面試中排名前10的演算法相關的概念，我會透過一些簡單的例子來闡述這些概念。由於完全掌握這些概念需要更多的努力，因此這份清單只是作為一個介紹。本文將從Java的角度看問題，包含下面的這些概念：

1. 字串

如果IDE沒有程式碼自動補全功能，所以你應該記住下面的這些方法。

toCharArray() // 获得字符串对应的char数组
Arrays.sort()  // 数组排序Arrays.toString(char[] a) // 数组转成字符串
charAt(int x) // 获得某个索引处的字符
length() // 字符串长度
length // 数组大小

2. 鍊錶

在Java中，鍊錶的實作非常簡單，每個節點Node都有一個值val和指向下個節點的連結next。

class Node {
    int val;
    Node next;
    Node(int x) {
        val = x;
        next = null;
    }
}

鍊錶兩個著名的應用是堆疊Stack和佇列Queue。

棧：

class Stack{
    Node top; 
    public Node peek(){
        if(top != null){
            return top;
        }
        return null;
    }
    public Node pop(){
        if(top == null){
            return null;
        }else{
            Node temp = new Node(top.val);
            top = top.next;
            return temp;
        }
    }
    public void push(Node n){
        if(n != null){
            n.next = top;
            top = n;
        }
    }
}

隊列：

class Queue{
    Node first, last;
    public void enqueue(Node n){
        if(first == null){
            first = n;
            last = first;
        }else{
            last.next = n;
            last = n;
        }
    }
    public Node dequeue(){
        if(first == null){
            return null;
        }else{
            Node temp = new Node(first.val);
            first = first.next;
            return temp;
        }
    }
}

3. 樹

這裡的樹通常是指二叉樹，每個節點都包含一個左孩子節點和右孩子節點，像下面這樣：

class TreeNode{
    int value;
    TreeNode left;
    TreeNode right;
}

下面是與樹相關的一些概念：

平衡vs. 非平衡：平衡二元樹中，每個節點的左右子樹的深度相差至多為1（1或0）。

滿二元樹（Full Binary Tree）：除葉子節點以為的每個節點都有兩個孩子。

完美二叉樹（Perfect Binary Tree）：是具有下列性質的滿二叉樹：所有的葉子節點都有相同的深度或處在同一層次，且每個父節點都必須有兩個孩子。

完全二叉樹（Complete Binary Tree）：在二叉樹中，可能除了最後一個，每一層都被完全填滿，且所有節點都必須盡可能想左靠。

譯者註：完美二元樹也隱約稱為完全二元樹。完美二元樹的一個例子是一個人在給定深度的祖先圖，因為每個人一定有兩個生父母。完全二元樹可以看成是可以有若干額外向左靠的葉子節點的完美二元樹。疑問：完美二元樹和滿二叉樹的差別？ （參考：http://xlinux.nist.gov/dads/HTML/perfectBinaryTree.html）

4. 圖

圖相關的問題主要集中在深度優先搜尋（depth first search）和廣度優先搜尋（breath first search）。

下面是一個簡單的圖廣度優先搜尋的實作。

1) 定義GraphNode

class GraphNode{ 
    int val;
    GraphNode next;
    GraphNode[] neighbors;
    boolean visited;
    GraphNode(int x) {
        val = x;
    }
    GraphNode(int x, GraphNode[] n){
        val = x;
        neighbors = n;
    }
    public String toString(){
        return "value: "+ this.val; 
    }
}

2) 定義一個佇列Queue

class Queue{
    GraphNode first, last;
    public void enqueue(GraphNode n){
        if(first == null){
            first = n;
            last = first;
        }else{
            last.next = n;
            last = n;
        }
    }
    public GraphNode dequeue(){
        if(first == null){
            return null;
        }else{
            GraphNode temp = new GraphNode(first.val, first.neighbors);
            first = first.next;
            return temp;
        }
    }
}

3) 用佇列Queue實作廣度優先搜尋

public class GraphTest {
    public static void main(String[] args) {
        GraphNode n1 = new GraphNode(1); 
        GraphNode n2 = new GraphNode(2); 
        GraphNode n3 = new GraphNode(3); 
        GraphNode n4 = new GraphNode(4); 
        GraphNode n5 = new GraphNode(5); 
        n1.neighbors = new GraphNode[]{n2,n3,n5};
        n2.neighbors = new GraphNode[]{n1,n4};
        n3.neighbors = new GraphNode[]{n1,n4,n5};
        n4.neighbors = new GraphNode[]{n2,n3,n5};
        n5.neighbors = new GraphNode[]{n1,n3,n4};
        breathFirstSearch(n1, 5);
    }
    public static void breathFirstSearch(GraphNode root, int x){
        if(root.val == x)
            System.out.println("find in root");
        Queue queue = new Queue();
        root.visited = true;
        queue.enqueue(root);
        while(queue.first != null){
            GraphNode c = (GraphNode) queue.dequeue();
            for(GraphNode n: c.neighbors){
                if(!n.visited){
                    System.out.print(n + " ");
                    n.visited = true;
                    if(n.val == x)
                        System.out.println("Find "+n);
                    queue.enqueue(n);
                }
            }
        }
    }
}

Output:

: value 5

2   value: 4

5. 排序

下面是不同排序演算法的時間複雜度，你可以去wiki看一下這些演算法的基本思想。

另外，這裡有一些實作/示範：: Counting sort、Mergesort、 Quicksort、 InsertionSort。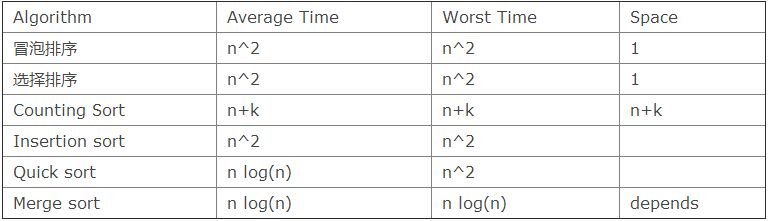

《視覺直觀感受7 種常用的排序演算法》

《影片: 6分鐘示範15種排序演算法》

6. 遞歸 vs. 迭代

對程式設計師來說，與生俱來應該是一個與生俱來的思想（a built-in thought），可以用一個簡單的例子來說明。

問題： 有n步台階，一次只能上1步或2步，共有多少種走法。

步驟1:找到走完前n步台階和前n-1步台階之間的關係。

為了走完n步台階，只有兩種方法：從n-1步台階爬1步走到或從n-2步台階處爬2步走到。如果f(n)是爬到第n步台階的方法數，那麼f(n) = f(n-1) + f(n-2)。

步驟2: 確保開始條件是正確的。

f(0) = 0;

f(1) = 1;

public static int f(int n){
    if(n <= 2) return n;
    int x = f(n-1) + f(n-2);
    return x;
}

遞歸方法的時間複雜度是n的指數級，因為有很多冗餘的計算，如下：

f(5)
f(4) + f(3)
f(3) + f(2) + f(2) + f(1)
f(2) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)
f(1) + f(0) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)

直接的想法是將遞歸轉換為迭代：

public static int f(int n) {
    if (n <= 2){
        return n;
    }
    int first = 1, second = 2;
    int third = 0;
    for (int i = 3; i <= n; i++) {
        third = first + second;
        first = second;
        second = third;
    }
    return third;
}

對這個例子而言，迭代花費的時間更少，你可能也想看看Recursion vs Iteration。

7. 動態規劃

動態規劃是解決以下這些性類型問題的技術：

一個問題可以透過更小子問題的解決方法來解決（譯者註：即問題的最優解包含了其子問題的最優解，也就是最優子結構性質）。

有些子問題的解可能需要計算多次（譯者註：也就是子問題重疊性質）。

子問題的解儲存在一張表格裡，這樣每個子問題只用計算一次。

需要額外的空間以節省時間。

爬台階問題完全符合上面的四條性質，因此可以用動態規劃法來解決。

public static int[] A = new int[100];
public static int f3(int n) {
    if (n <= 2)
        A[n]= n;
    if(A[n] > 0)
        return A[n];
    else
        A[n] = f3(n-1) + f3(n-2);//store results so only calculate once!
    return A[n];
}

8. 位操作

位元運算子：

获得给定数字n的第i位：(i从0计数并从右边开始)

public static boolean getBit(int num, int i){
    int result = num & (1<<i);
    if(result == 0){
        return false;
    }else{
        return true;
    }

例如，获得数字10的第2位：

i=1, n=10
11010&10=10
10 is not 0, so return true;

9. 概率问题

解决概率相关的问题通常需要很好的规划了解问题（formatting the problem），这里刚好有一个这类问题的简单例子：

一个房间里有50个人，那么至少有两个人生日相同的概率是多少？（忽略闰年的事实，也就是一年365天）

计算某些事情的概率很多时候都可以转换成先计算其相对面。在这个例子里，我们可以计算所有人生日都互不相同的概率，也就是：365/365 * 364/365 * 363/365 * … * (365-49)/365，这样至少两个人生日相同的概率就是1 – 这个值。

public static double caculateProbability(int n){
    double x = 1; 
    for(int i=0; i<n; i++){
        x *=  (365.0-i)/365.0;
    }
    double pro = Math.round((1-x) * 100);
    return pro/100;

calculateProbability(50) = 0.97

10. 排列组合

组合和排列的区别在于次序是否关键。

如果你有任何问题请在下面评论。

参考/推荐资料：
1. Binary tree
2. Introduction to Dynamic Programming
3. UTSA Dynamic Programming slides
4. Birthday paradox
5. Cracking the Coding Interview: 150 Programming Interview Questions and Solutions, Gayle Laakmann McDowell