js為什麼不能正確處理小數運算? _javascript技巧
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB原創
- 2016-05-16 15:22:591510瀏覽
var sum = 0;
for(var i = 0; i < 10; i++) {
sum += 0.1;
}
console.log(sum);
上面的程式會輸出1嗎?
在 你有必要知道的 25 個 JavaScript 面試題 一文中,第 8 題淺顯的說了下 js 為什麼不能正確處理小數運算的問題。今天重拾舊題,更深層的剖析下這個問題。
但要先說明的是,不能正確處理小數的運算並不是 JavaScript 語言本身的設計錯誤,其它高級程式語言,如C,Java等,也是不能正確處理小數運算的:
#include <stdio.h>
void main(){
float sum;
int i;
sum = 0;
for(i = 0; i < 100; i++) {
sum += 0.1;
}
printf('%f\n', sum); //10.000002
}
數在電腦內部的表示
我們都知道,用高階程式語言寫的程式需要經過解釋、編譯等操作轉變成CPU(Central Processing Unit) 可以辨識的機器語言才能運行,而對CPU 來說,它不識別數的十進制、八進制和十六進制等,我們在程式中聲明的這些進制數都會被轉換成二進制數來運算。
為什麼不是要轉換成三進位數來運算呢?
電腦內部是由很多的 IC (Integrated Circuit: 積體電路) 這種電子元件構成的,它的長相大概是這樣子:
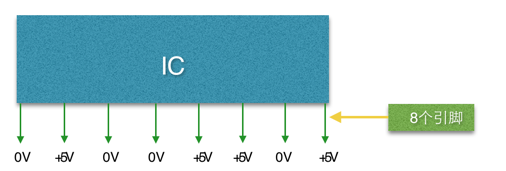
IC 有很多種形狀,在其兩側或內部並排排列著很多引腳(圖示只畫出了一側)。 IC 的所有引腳,只有直流電壓 0V 或 5V 兩個狀態,即 IC 引腳只能表示兩個狀態。 IC 的這個特性就決定了電腦內部的資料只能用二進位數處理。
由於1 位元(一個腳位)只能表示兩個狀態,所以二進位的計算方式就變成了 0、1、10、11、100….這種形式:
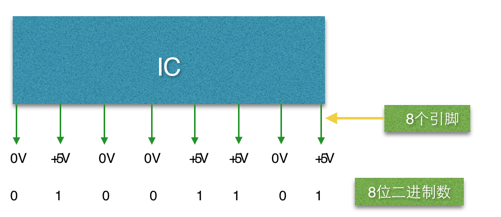
所以,在數的運算中,所有操作數都會被轉成二進制數參與運算,如39,會被轉換成二進制 00100111
小數的二進位表示
如前文所說,程式中的資料都會被轉換成二進制數,小數參與運算時,也會被轉成二進制,如十進制的11.1875 會被轉換成1101.0010。
小數點後4 位用二進制數表示的數值範圍是0.0000~0.1111,因此,這只能表示0.5、0.25、0.125、0.0625 這四個十進制數以及小數點後面的位權組合(相加)而成的小數:

從上表可以看出,十進制數0 的下一位是0.0625,所以,0~0.0625 之間的小數,就無法用小數點後4 位數的二進制數表示;如果增加二進制數小數點後面的位數,與其相對應的十進制數的個數也會增加,但無論增加多少位,都無法得到0.1 這個結果。實際上,0.1 轉換成二進位是 0.00110011001100110011… 注意 0011 是無限重複的:
console.log(0.2+0.1); //操作数的二进制表示 0.1 => 0.0001 1001 1001 1001…(无限循环) 0.2 => 0.0011 0011 0011 0011…(无限循环)
js 的 Number 型別並沒有像 C / Java 等分整型、單精確度、雙精確度等,而是統一表現為雙精確度浮點型。依照IEEE 的規定,單精確度浮點數以32 位元表示全體小數,而雙精確度浮點數用64 位元表示全體小數,而浮點數由符號、尾數、指數和基數組成,所以並不是所有的位數都用來表示小數,符號、指數等也要佔據位數,基數不佔據位數:

雙精度浮點數的小數部分最多支援52 位,所以兩者相加之後得到這麼一串0.0100110011001100110011001100110011001100…因浮點數小數位的限製而截斷的二進制數字,這時候轉換為十點就成了0.30000000000000004。
總結
js 不能正確處理小數運算,包括其它高級程式語言一樣,這不是語言本身的設計錯誤,而是計算機內部本身就不能正確處理小數的運算,對小數的運算往往會得到意想不到的結果,因為並不是所有的十進制小數能被二進位表示。
以上就是本文的全部內容,希望對大家的學習有所幫助。

