canvas差分函數的妙用

在這篇文章中我們就分析這種效果是如何實現的，如果你對源碼比較懵逼，相信看完解析就會恍然大悟。先上效果圖：

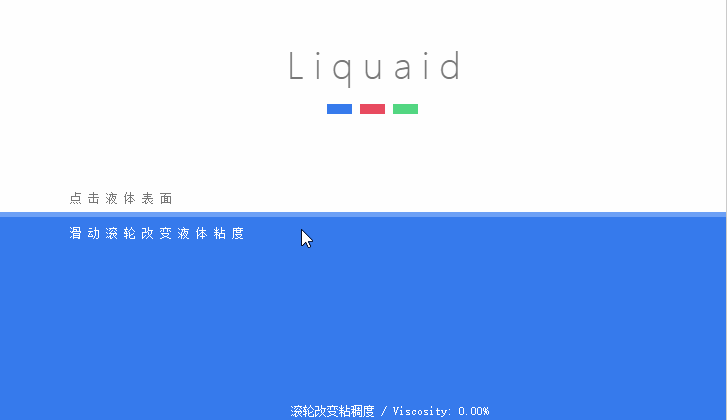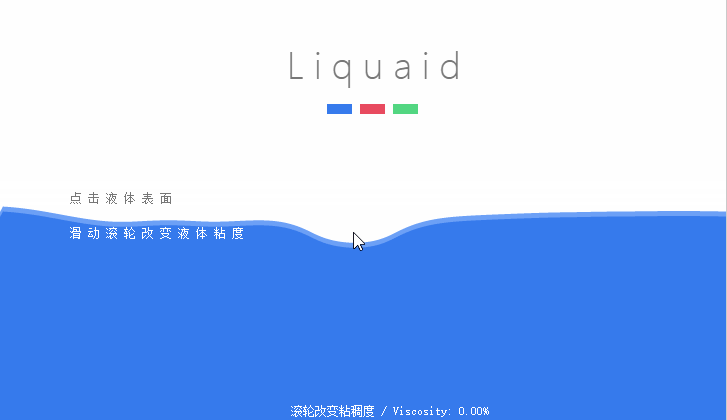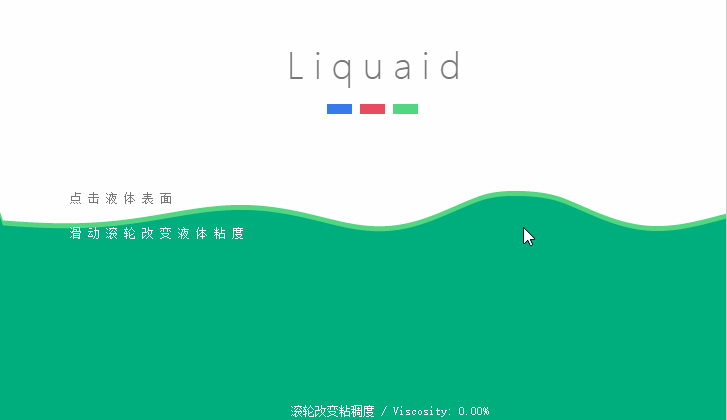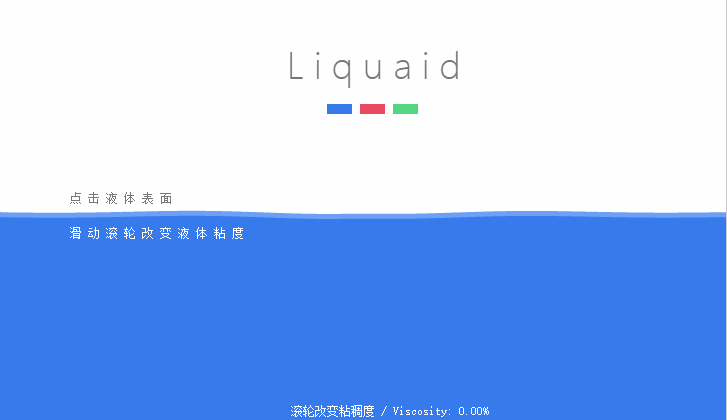
1.原理分析

相比與上篇文章中簡陋的水波動畫的效果，本文的動畫效果不僅能夠和滑鼠進行交互，而且波浪的形成更加自然，更加符合物理規律。整個動畫的形成過程就如動圖中所展示的那樣，在液面的位置點擊滑鼠，此處的液面就會有一個比較大的起伏，然後此處的震動會向兩邊傳播，隨著能量的衰減，後面的震動幅度會越來越下，最後能量衰減到零，頁面趨於平靜。聽起來是不是很玄乎，感覺很高深！毛主席告訴我們千萬不要被物體的表面現象所迷惑（誰知道是誰說的呢o(^▽^)o）。下面我們就來一步一步的分析，這其中的原理。

首先，在靜止狀態下我們可以看到整個液面就等於是個長方形。而當我們點擊液面的位置時，這個矩形就發生了相對應的變化。但其實並不是整個矩形都發生了變化，而只是矩形的上邊發生了變化。那是如何做到僅僅讓矩形的上邊改變的呢？秘訣就在長方形的上邊並不是簡單的從左邊的點lineTo()到右邊的點。而是由很多的點lineTo()組成。這樣講可能不太理解，看圖說話：

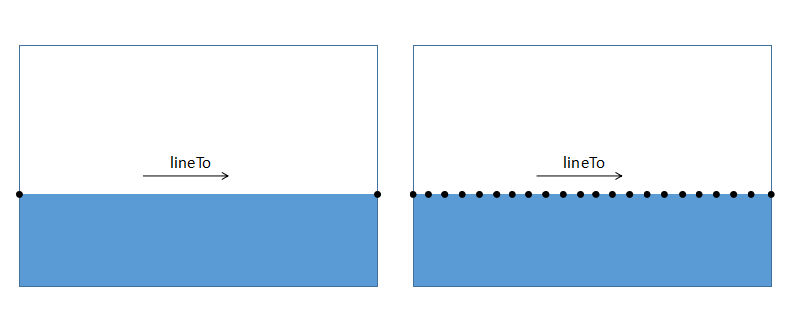
在上部我們設定了很多的點，這些點的縱座標都是一樣的，只是在水平方向相隔一定的間距。這樣在靜止的狀態下，我們就可以它看見與普通的矩形別無二致。而改變這些點的位置時我們就能同時改變矩形的形狀，進而形成不同的效果。

2.差分方程式

說到差分方程式也許很多人會頭疼，不過也沒本法，痛就痛會吧！這個知識點在高數裡講微分方程那一節，如果不明白，就算了吧！記住下面的用法也不錯，不過為了逼格我們還是簡單的介紹下。

在數學上，遞推關係（recurrence relation），也就是差分方程式（difference equation），是一種遞推定義一個序列的方程式：序列的每一項目是定義為前一項的函數。某些簡單定義的遞推關係式可能會表現出非常複雜的（混沌的）性質，他們屬於數學中的非線性分析領域。

記住一點，序列的每一項是定義為前一項的函數，我們用的就是這個原理。他的圖像如果用matalab來繪製就是下面這樣：

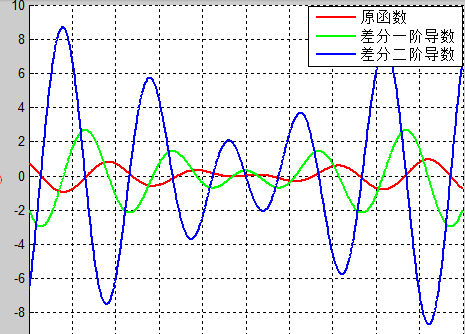
只關注原函數，紅色的那條曲線就可以了，是不是特別像水波。我們要做的就是讓那一堆點照這樣的波形去排列。

3.程式碼實作

1.準備工作

下面就到了大家最喜歡的程式碼時間。首先，我們創建一個點類Vertexes, 它的作用就是定義並更新那一堆點，程式碼在vertex.js中，如下：

function Vertex(x,y,baseY){
        this.baseY = baseY;         //基线
        this.x = x;                 //点的坐标
        this.y = y;            
        this.vy = 0;                //竖直方向的速度
        this.targetY = 0;           //目标位置
        this.friction = 0.15;       //摩擦力
        this.deceleration = 0.95;   //减速
    }
//y坐标更新
Vertex.prototype.updateY = function(diffVal){
        this.targetY = diffVal + this.baseY;   //改变目标位置
        this.vy += (this.targetY - this.y);       //速度
        this.vy *= this.deceleration;
        this.y += this.vy * this.friction;     //改变坐标竖直方向的位置
    }

我們要用這個函數去創建那一堆點。回到我們的主文件index.js中。我們先初始化一些要用的東西：

var canvas = document.getElementById('canvas'),
    ctx = canvas.getContext('2d'),
    W = window.innerWidth;
    H = window.innerHeight;

    canvas.width = W;
    canvas.height = H;

var color1 = "#6ca0f6",    //矩形1的颜色
    color2 = "#367aec";   //矩形2的颜色
    
var vertexes = [],    //顶点坐标
    verNum = 250,     //顶点数
    diffPt = [],      //差分值

然后，创建点并把它push进vertexes中，同时也创建相应数量的差分值，同样把它放到diffPt数组中，这样每个点都有了对应的差分值。

for(var i=0; i<verNum; i++){
    vertexes[i] = new Vertex(W/(verNum-1)*i, H/2, H/2);
    diffPt[i] = 0;                                         //初始值都为0
}

结果是，每个顶点的y坐标都在（H/2）的高度，水平坐标每隔一定的间隔取一个点。在这里是每隔4.5个像素取一个点，这与你canvas的宽度和点的数目有关。这样我们就把点创建完成了，来绘制一下看看效果。

代码如下：

function draw(){
        
        //矩形1
        ctx.save()
        ctx.fillStyle = color1;
        ctx.beginPath();
        ctx.moveTo(0, H);
        ctx.lineTo(vertexes[0].x, vertexes[0].y);
        for(var i=1; i<vertexes.length; i++){
            ctx.lineTo(vertexes[i].x, vertexes[i].y);
        }
        ctx.lineTo(W,H);
        ctx.lineTo(0,H);
        ctx.fill();
        ctx.restore();
        
        //矩形2
        ctx.save();
        ctx.fillStyle = color2;
        ctx.beginPath();
        ctx.moveTo(0, H);
        ctx.lineTo(vertexes[0].x, vertexes[0].y+5);
        for(var i=1; i<vertexes.length; i++){
            ctx.lineTo(vertexes[i].x, vertexes[i].y+5);
        }
        ctx.lineTo(W, H);
        ctx.lineTo(0, H);
        ctx.fill();
        ctx.restore();
}

就像你看到的那样此时我们的液面完全是静止的（因为没更新点嘛）。之所以要绘制两个矩形，你看看效果图就明白了，只是为了更好看，你完全可以绘制第三层，第四层。下面我们就来更新这些点的坐标。

2.核心代码

点的更新我们放在了update函数中。首先，我们设置一个初始的震荡点,缓冲变量和初始差分值。

var vPos = 125;  //震荡点
var dd = 15;     //缓冲
var autoDiff = 1000;  //初始差分值

这里的震荡点就是我们的起震位置，意思是vertexes中的第125号点开始起震，它对应的差分值就是autoDiff。它的改变会引起其他点的变化，从而达到更新其他差分值的效果。

function update(){
        autoDiff -= autoDiff*0.9;        //1
        diffPt[vPos] = autoDiff;         

        //左侧
        for(var i=vPos-1; i>0; i--){     //2
            var d = vPos-i;
            if(d > dd){
                d=dd;
            }
            diffPt[i]-=(diffPt[i] - diffPt[i+1])*(1-0.01*d);
        }
        //右侧
        for(var i=vPos+1; i<verNum; i++){   //3
            var d = i-vPos;
            if(d>dd){
                d=dd;
            }
            diffPt[i] -= (diffPt[i] - diffPt[i-1])*(1-0.01*d);
        }

        //更新Y坐标
        for(var i=0; i<vertexes.length; i++){  //4
            vertexes[i].updateY(diffPt[i]);
        }
    }

现在我们对上面的部分做详细解释：
代码1： 我们设置了起震位置的差分偏移量为autoDiff=100,注意autoDiff -= autoDiff*0.9;, 也就是说它的值每一帧都会变化。

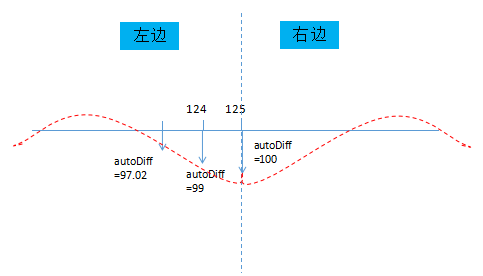
代码2：为起震位置的左边，主要关注diffPt[i]-=(diffPt[i] - diffPt[i+1])*(1-0.01*d);这一行。i的起始位置为124，默认差分值为0。稍作简单推算，你会发现，经过更新后第124号点的差分值为99，同理第123号为97.02。以此类推，我们就可以得到第一帧的所有点的差分值。右边同理。

代码4：在得到第一帧的差分值后就该调用每个点的更新函数了，并且传入计算好的差分值。形成的效果如下图所示

看一下updateY函数，我们把目标位置targetY设置为差分值diffVal和基线baseY的和。然后，通过距离计算需要运动的速度vy,最后将速度作用于点的纵坐标。这一段是不是与弹性动画缓动动画那一节很相似呢？

在缓冲系数dd的作用下，两侧的波会在扩散的过程中越来越小，最后趋近于0.我们也是通过这个变量去控制液体的粘度系数，达到粘稠度高的物体扩散的越缓慢并且起伏比较低，粘稠度低的物体扩散迅速但起伏大的效果。

随后，因为autoDiff的不断衰减，不同幅值波形的叠加形成波浪效果，最终衰减到0.液面也就趋于平静了。

现在，我们把update()和draw()放入动画循环中你就会看到水波起伏然后趋于平静的效果。

(function drawframe(){
        ctx.clearRect(0, 0, W, H);
        window.requestAnimationFrame(drawframe, canvas);
        update()
        draw();
    })()

3.鼠标交互

上面的代码已经实现了波浪动画的效果，但是震荡完成后就平静了，不会再发生震荡的效果。这一步我们就来实现点哪，哪震的效果。实现的思路很简单：水波之所以区域平静是因为起震位置的差分值不断衰减的结果，我们只需要在点击鼠标的位置重设autoDiff就可以了。此外，起震点的位置也要变成鼠标点击的位置。代码如下：

canvas.addEventListener('mousedown', function(e){
        var mouse = {x:null, y:null};

        if(e.pageX||e.pageY){
            mouse.x = e.pageX;
            mouse.y = e.pageY;
        }else{
            mouse.x = e.clientX + document.body.scrollLeft +document.documentElement.scrollLeft;
            mouse.y = e.clientY + document.body.scrollTop +document.documentElement.scrollTop;
        }

        //重设差分值
        if(mouse.y>(H/2-50) && mouse.y<(H/2 +50)){
            autoDiff = 1000;
            vPos = 1 + Math.floor((verNum - 2) * mouse.x / W);
            diffPt[vPos] = autoDiff;
        }

        console.log(mouse.x, mouse.y)

    }, false)

在获取鼠标位置这里应该注意一点，我们没有减去canvas的偏移量，这是因为在这里canvas做的是全屏设置。所以，如果你的画布并不是全屏大小，建议你使用我们的utils.js文件中的方法captureMouse来获取鼠标的坐标。

另外在判断鼠标是否点击在了液面上，我们设定了一个比较宽的范围，上下共100px。这样做的目的是让用户很容易就能触发这个事件，而不是只在页面那唯一的一个值上才能触发。这种做法相信你以前做过，对于比较小的物体我们会遮罩一个大一些的透明物体，然后在该物体上做事件的触发，便于用户操作。