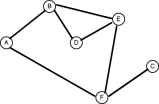
PHP主| PHP DEV的數據結構：圖形-php教程-PHP中文網

首頁

後端開發

php教程

PHP主| PHP DEV的數據結構：圖形

Joseph Gordon-Levitt

Feb 23, 2025 am 08:49 AM

PHP主| PHP DEV的數據結構：圖形

鑰匙要點

圖理論的常見應用是在任意兩個節點之間找到最少數量的啤酒花（即最短路徑）。這可以使用廣度優先的搜索來實現，這涉及從指定的根節點從級別穿越圖形級別。此過程需要保持未訪問的節點的隊列。 > Dijkstra的算法被廣泛用於查找圖中任何兩個節點之間的最短或最佳路徑。這涉及檢查從源節點開始的所有可能對頂點之間的每個邊緣，並保持最短的總距離的更新的頂點，直到達到目標節點為止。

在我以前的一篇文章中，我向您介紹了樹數據結構。現在，我想探索一個相關的結構 - 圖。圖具有許多現實世界應用程序，例如網絡優化，流量路由和社交網絡分析。 Google的Pagerank，Facebook的Graph Search以及Amazon和Netflix的建議是圖形驅動應用程序的一些示例。在本文中，我將探討使用圖形的兩個常見問題 - 啤酒花數量最少和最短路徑問題。圖是一種數學結構，用於建模鍵/值對之間的關系。圖包含一組>頂點（節點）和連接它們的任意數量的 edges（線）。這些邊緣可以指向或無向。導向邊緣只是兩個頂點之間的邊緣，而邊緣A→B不與B→A相同。無方向的邊緣沒有方向或方向；邊緣A-B等於B-A。我們上次了解到的樹結構可以被視為一種無向圖的類型，其中每個頂點通過簡單路徑連接到至少一個其他頂點。圖形也可以加權或未加權。加權圖或網絡是將重量或成本值分配給其每個邊緣的一個網絡。加權圖通常用於確定最佳路徑，最優勢或兩個點之間的最低“成本”路徑。 GoogleMap的驅動方向是使用加權圖的示例。最少的啤酒花

圖理論的常見應用是在任意兩個節點之間找到最少的啤酒花。與樹一樣，圖形可以通過以下兩種方式之一進行遍歷：深度優先或廣度優先。我們在上一篇文章中介紹了深度優先的搜索，因此讓我們看一下廣度優先的搜索。考慮以下圖：

PHP主| PHP DEV的數據結構：圖形為了簡單起見，讓我們假設該圖是

的 - 即，任何方向的邊緣是相同的。我們的任務是在任意兩個節點之間找到最少的啤酒花。在廣度優先的搜索中，我們從根節點（或指定為根的任何節點）開始，然後按級別沿著樹的水平沿我們的方式進行工作。為了做到這一點，我們需要一個隊列來維護未訪問的節點的列表，以便我們可以在每個級別後回溯和處理它們。一般算法看起來像這樣：但是，我們怎麼知道哪些節點相鄰，更不用說未訪問的而不首先遍歷圖形呢？這使我們解決瞭如何建模圖數據結構的問題。

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

代表圖形

通常有兩種表示圖形的方法：作為鄰接矩陣或鄰接列表。上面的圖表示為鄰接列表，如下所示：

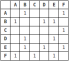
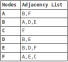PHP主| PHP DEV的數據結構：圖形該圖表示為矩陣，其中1表示2個頂點之間的邊緣的“發生率”：

PHP主| PHP DEV的數據結構：圖形

鄰接列表更具空間效率，尤其是對於大多數頂點沒有連接的稀疏圖，而鄰接矩陣有助於更快的查找。最終，表示形式的選擇將取決於可能需要哪種類型的圖形操作。讓我們使用鄰接列表來表示圖表：

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

現在，讓我們看看一般廣度優先搜索算法的實現是什麼樣的：

<span><span><?php </span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span></span>

運行以下示例，我們得到：

<span><span><?php </span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span></span>

如果我們使用堆棧而不是隊列，則遍歷將成為深度優先的搜索。

找到最短路徑

另一個常見的問題是找到任何兩個節點之間的最佳路徑。早些時候，我提到了GoogleMap的行駛方向，以此為例。其他應用程序包括規劃旅行行程，道路交通管理以及火車/公共汽車計劃。解決此問題的最著名算法之一是由一位29歲的計算機科學家以Edsger W. Dijkstra的名義發明的。總的來說，Dijkstra的解決方案涉及檢查從源節點開始的所有可能的頂點之間的每個邊緣，並保持最短的總距離的更新的頂點，直到達到目標節點，或者無法達到目標節點，任何情況下的情況下。有幾種方法可以實施該解決方案，實際上，在1959年，使用Minheaps，Priorityqueues和Fibonacci堆的多年以來，都對Dijkstra的原始算法做出了。一些改進的性能，而另一些則旨在解決Dijkstra解決方案中的缺點，因為它僅適用於正加權圖（權重為正值）。這是一個（正）加權圖的示例：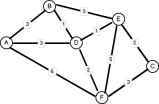

PHP主| PHP DEV的數據結構：圖形

我們可以將此圖表示為鄰接列表，如下所示：

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

這是使用PriorityQueue來維護所有“不優化”頂點的列表的實現：

<span><span><?php </span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span></span>

如您所見，Dijkstra的解決方案只是廣度優先搜索的變體！運行以下示例會產生以下結果：

<span><span><?php </span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span></span>

摘要

在本文中，我介紹了圖理論的基礎知識，兩種表示圖形的方法以及圖理論應用中的兩個基本問題。我向您展示瞭如何使用廣度優先的搜索來找到任何兩個節點之間最少的啤酒花，以及如何使用Dijkstra的解決方案來找到任何兩個節點之間的最短路徑。通過fotolia 圖像經常詢問數據結構中圖的問題（常見問題解答）

數據結構中的圖和樹之間有什麼區別？樹是一種類型，但並非所有圖形都是樹。樹是沒有任何週期的連接圖。它具有帶根節點和子節點的層次結構。樹上的每個節點都有一個獨特的路徑。另一方面，圖可以具有循環，其結構更為複雜。它可以連接或斷開連接，節點之間可以具有多個路徑。列表。鄰接矩陣是大小為v x v的2D數組，其中v是圖中的頂點數。如果頂點I和J之間有邊緣，則第I和J列的交點處的單元格為1，否則為0。鄰接列表是鏈接列表的數組。數組的索引代表一個頂點，其鏈接列表中的每個元素代表與頂點形成邊緣的其他頂點。是數據結構中幾種類型的圖形。一個簡單的圖是一個沒有循環的圖形，在任何兩個頂點之間不超過一個邊緣。多編碼可以在頂點之間具有多個邊緣。完整的圖是一個簡單的圖形，其中每對頂點都通過邊緣連接。加權圖為每個邊緣分配一個權重。有向圖（或Digraph）具有方向的邊緣。邊緣從一個頂點到另一個頂點。

在計算機科學中的許多應用中，都使用了圖表中圖中圖的應用？它們在社交網絡中用於表示人們之間的聯繫。它們用於網絡爬行中訪問網頁並構建搜索索引。它們用於網絡路由算法中，以找到兩個節點之間的最佳路徑。它們在生物學中用於建模和分析生物網絡。它們也用於計算機圖形和物理模擬中。

>圖形遍曆算法是什麼？

>有兩個主要的圖形遍曆算法：Depth-First Search（DFS）和廣度優先搜索（BFS）。 DFS在回溯之前盡可能沿每個分支探索。它使用堆棧數據結構。 BFS探索當前深度的所有頂點，然後才能進入下一個級別。它使用隊列數據結構。

如何在Java中實現圖形？ hashmap中的每個鍵都是頂點，其值是一個鏈接列表，包含其連接到的頂點。

>什麼是兩部分圖？

二鍵圖是一個圖形，是一個圖形的圖形。被分為兩個不相交的集合，使每個邊緣在一個集合中連接一個頂點與另一組頂點連接。沒有邊界在同一集合中連接頂點。

什麼是子圖？

一個子圖是一個圖形，是另一個圖的一部分。它具有原始圖的某些（或全部）頂點，以及原始圖的某些（或全）邊緣。

>圖中的一個週期是什麼？一條從同一頂點開始和結束的路徑，至少具有一個邊。的連續的頂點通過邊緣連接。

以上是PHP主| PHP DEV的數據結構：圖形的詳細內容。更多資訊請關注PHP中文網其他相關文章！

陳述

本文內容由網友自願投稿，版權歸原作者所有。本站不承擔相應的法律責任。如發現涉嫌抄襲或侵權的內容，請聯絡admin@php.cn

unset（）和session_destroy（）有什麼區別？May 04, 2025 am 12:19 AM

Thedifferencebetweenunset()andsession_destroy()isthatunset()clearsspecificsessionvariableswhilekeepingthesessionactive,whereassession_destroy()terminatestheentiresession.1)Useunset()toremovespecificsessionvariableswithoutaffectingthesession'soveralls

在負載平衡的情況下，什麼是粘性會話（會話親和力）？May 04, 2025 am 12:16 AM

stickysessensureuserRequestSarerOutedTothesMeServerForsessionDataConsisterency.1）sessionIdentificeAssificationAssigeaSsignAssignSignSuserServerServerSustersusiseCookiesorUrlModifications.2）一致的ententRoutingDirectSsssssubsequeSssubsequeSubsequestrequestSameSameserver.3）loadBellankingDisteributesNebutesneNewuserEreNevuseRe.3）

PHP中有哪些不同的會話保存處理程序？May 04, 2025 am 12:14 AM

phpoffersvarioussessionsionsavehandlers：1）文件：默認，簡單的ButMayBottLeneckonHigh-trafficsites.2）Memcached：高性能，Idealforsforspeed-Criticalapplications.3）REDIS：redis：similartomemememememcached，withddeddeddedpassistence.4）withddeddedpassistence.4）databases：gelifforcontrati forforcontrati，有用

PHP中的會話是什麼？為什麼使用它們？May 04, 2025 am 12:12 AM

PHP中的session是用於在服務器端保存用戶數據以在多個請求之間保持狀態的機制。具體來說，1)session通過session_start()函數啟動，並通過$_SESSION超級全局數組存儲和讀取數據；2)session數據默認存儲在服務器的臨時文件中，但可通過數據庫或內存存儲優化；3)使用session可以實現用戶登錄狀態跟踪和購物車管理等功能；4)需要注意session的安全傳輸和性能優化，以確保應用的安全性和效率。

說明PHP會話的生命週期。May 04, 2025 am 12:04 AM

PHPsessionsstartwithsession_start(),whichgeneratesauniqueIDandcreatesaserverfile;theypersistacrossrequestsandcanbemanuallyendedwithsession_destroy().1)Sessionsbeginwhensession_start()iscalled,creatingauniqueIDandserverfile.2)Theycontinueasdataisloade

絕對會話超時有什麼區別？May 03, 2025 am 12:21 AM

絕對會話超時從會話創建時開始計時，閒置會話超時則從用戶無操作時開始計時。絕對會話超時適用於需要嚴格控制會話生命週期的場景，如金融應用；閒置會話超時適合希望用戶長時間保持會話活躍的應用，如社交媒體。

如果會話在服務器上不起作用，您將採取什麼步驟？May 03, 2025 am 12:19 AM

服務器會話失效可以通過以下步驟解決：1.檢查服務器配置，確保會話設置正確。 2.驗證客戶端cookies，確認瀏覽器支持並正確發送。 3.檢查會話存儲服務，如Redis，確保其正常運行。 4.審查應用代碼，確保會話邏輯正確。通過這些步驟，可以有效診斷和修復會話問題，提升用戶體驗。

session_start（）函數的意義是什麼？May 03, 2025 am 12:18 AM

session_start（）iscucialinphpformanagingusersessions.1）ItInitiateSanewsessionifnoneexists，2）resumesanexistingsessions，and3）setsasesessionCookieforContinuityActinuityAccontinuityAcconActInityAcconActInityAcconAccRequests，EnablingApplicationsApplicationsLikeUseAppericationLikeUseAthenticationalticationaltication and PersersonalizedContentent。

See all articles