了解快速排序演算法（附Java範例）

QuickSort 演算法詳解：高效率的排序利器

快速排序 (QuickSort) 是一種基於分治策略的高效排序演算法。分治法將問題分解成更小的子問題，分別解決這些子問題，然後組合子問題的解得到最終解。在快速排序中，陣列透過選擇一個分區元素來劃分，該元素決定數組的分割點。在劃分之前，分區元素的位置會重新排列，使其位於大於它的元素之前，小於它的元素之後。左右子數組將以這種方式遞歸劃分，直到每個子數組只包含一個元素，此時數組已排序。

快速排序工作原理

讓我們以升序排序以下數組為例：

步驟 1：選擇樞軸元素

我們選擇最後一個元素作為樞軸：

步驟 2：重新排列樞軸元素

我們將樞軸元素放置在其大於它的元素之前，小於它的元素之後。為此，我們將遍歷數組，並將樞軸與它之前的每個元素進行比較。如果找到一個大於樞軸的元素，我們為它建立一個第二個指標：

如果找到一個小於樞軸的元素，我們將它與第二個指標交換：

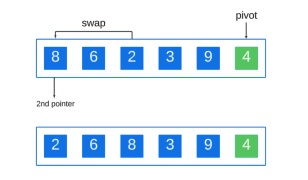
重複此過程，將下一個大於樞軸的元素設定為第二個指針，如果找到小於樞軸的元素則進行交換：

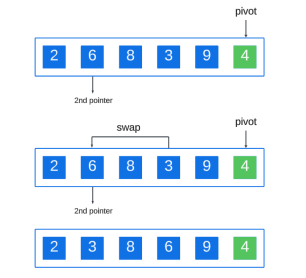
繼續此過程直到到達陣列的末端：

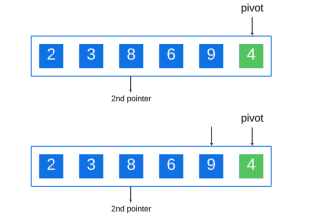
完成元素比較後，小於樞軸的元素已移動到右側，然後我們將樞軸與第二個指針交換：

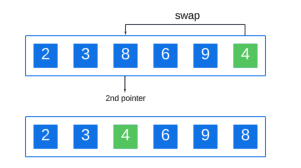
步驟 3：分割數組

根據分區索引劃分數組。如果我們將數組表示為arr[start..end]，則透過分區劃分數組，可以得到左子數組arr[start..partitionIndex-1] 和右子數組arr[partitionIndex 1..end]。

以這種方式繼續劃分子數組，直到每個子數組只包含一個元素：

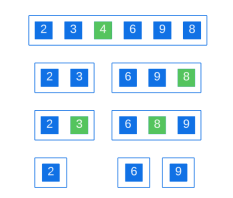
此時，陣列已排序。

快速排序程式碼實作

<code class="language-java">import java.util.Arrays;

public class QuickSortTest {
    public static void main(String[] args){
        int[] arr = {8, 6, 2, 3, 9, 4};
        System.out.println("未排序数组: " + Arrays.toString(arr));
        quickSort(arr, 0, arr.length-1);
        System.out.println("已排序数组: " + Arrays.toString(arr));
    }

    public static int partition(int[] arr, int start, int end){
        // 将最后一个元素设置为枢轴
        int pivot = arr[end];
        // 创建指向下一个较大元素的指针
        int secondPointer = start-1;

        // 将小于枢轴的元素移动到枢轴左侧
        for (int i = start; i < end; i++){
            if (arr[i] < pivot){
                secondPointer++;
                // 交换元素
                int temp = arr[secondPointer];
                arr[secondPointer] = arr[i];
                arr[i] = temp;
            }
        }
        // 将枢轴与第二个指针交换
        int temp = arr[secondPointer+1];
        arr[secondPointer+1] = arr[end];
        arr[end] = temp;
        // 返回分区索引
        return secondPointer+1;
    }

    public static void quickSort(int[] arr, int start, int end){
        if (start < end){
            // 找到分区索引
            int partitionIndex = partition(arr, start, end);
            // 递归调用快速排序
            quickSort(arr, start, partitionIndex-1);
            quickSort(arr, partitionIndex+1, end);
        }
    }
}</code>

程式碼解讀

quickSort 方法：先呼叫 partition 方法將陣列分成兩個子數組，然後遞歸呼叫 quickSort 對左右子數組進行排序。這個過程持續進行，直到所有子數組都只包含一個元素，此時數組已排序。

partition 方法：負責將陣列分成兩個子數組。它首先設定樞軸和下一個較大元素的指針，然後遍歷數組，將小於樞軸的元素移動到左側。之後，它將樞軸與第二個指針交換，並返回分區位置。

運行以上程式碼，控制台將輸出以下內容：

未排序數組: [8, 6, 2, 3, 9, 4] 已排序數組: [2, 3, 4, 6, 8, 9]

時間複雜度

最佳情況 (O(n log n))：當樞軸每次都將陣列分成兩個幾乎相等的部分時，就會出現最佳情況。

平均情況 (O(n log n))：在平均情況下，樞軸將陣列分成兩個不相等的部分，但遞歸深度和比較次數仍與 n log n 成正比。

最壞情況(O(n²))：當樞軸總是將陣列分成非常不相等的部分（例如，一部分只有一個元素，另一部分有n-1 個元素）時，就會出現最壞情況。例如，當排序一個逆序數組時，且樞軸選擇不佳時，就會發生這種情況。

空間複雜度 (O(log n))：快速排序通常就地實現，不需要額外的數組。

以上是了解快速排序演算法（附Java範例）的詳細內容。更多資訊請關注PHP中文網其他相關文章！