如何解析電腦程式碼，程式碼的出現 ay 3

解決了後來的一些《Advent of Code》挑戰後，我想重新回顧第 3 天，它提出了一個有趣的解析問題。這個任務涉及從嘈雜的輸入中提取有效的程式碼，這是解析器和詞法分析器開發中的一個很好的練習。和我一起探索應對這項挑戰的方法。

由 Microsoft Copilot 產生的圖像，顯示我對拼圖 (?) 的熱愛

當我第一次寫統治者DSL時，我依靠Hy來解析。然而，我最近對生成式人工智慧的探索引入了一種新的解析方法：使用 funcparserlib 函式庫產生程式碼。這次「程式碼挑戰」讓我能夠深入研究 funcparserlib 的複雜性，並對產生的程式碼的功能有更深入的掌握。

實作詞法分析器（詞法分析）

處理損壞的輸入的第一步是詞法分析（或標記化）。 詞法分析器（或分詞器）掃描輸入字串並將其分成單獨的標記，它們是進一步處理的基本構建塊。 token 表示輸入中有意義的單元，依其型別分類。對於這個謎題，我們對這些令牌類型感興趣：

• 運算子 (OP)： 這些代表函數名稱，例如 mul、do 和 don't。例如，輸入 mul(2, 3) 包含運算符標記 mul.
• 數字：這些是數值。例如，在輸入 mul(2, 3) 中，2 和 3 將被識別為數字標記。
• 逗號： 逗號字元 (,) 充當參數之間的分隔符號。
• 括號： 左括號（和右括號）定義函數呼叫的結構。
• 亂碼： 此類別包含與其他標記類型不符的任何字元或字元序列。這就是輸入的“損壞”部分出現的地方。例如，%$#@ 或任何隨機字母將被視為亂碼。

雖然 funcparserlib 經常在其教程中使用魔術字串，但我更喜歡更結構化的方法。魔術字串可能會導致拼字錯誤並使重構程式碼變得困難。使用 Enum 定義令牌類型有幾個優點：更好的可讀性、改進的可維護性和增強的類型安全性。以下是我如何使用枚舉定義令牌類型：

from enum import Enum, auto

class Spec(Enum):
    OP = auto()
    NUMBER = auto()
    COMMA = auto()
    LPAREN = auto()
    RPAREN = auto()
    GIBBERISH = auto()

透過使用 Spec.OP、Spec.NUMBER 等，我們避免了與使用純字串相關的歧義和潛在錯誤。

為了將 Enum 與 funcparserlib 無縫集成，我創建了一個名為 TokenSpec_ 的自訂裝飾器。此裝飾器可作為 funcparserlib 中原始 TokenSpec 函數的包裝器。它透過接受 Spec Enum 中的值作為 spec 參數來簡化標記定義。在內部，它會提取枚舉 (spec.name) 的字串表示形式，並將其與任何其他參數一起傳遞給原始 TokenSpec 函數。

from enum import Enum, auto

class Spec(Enum):
    OP = auto()
    NUMBER = auto()
    COMMA = auto()
    LPAREN = auto()
    RPAREN = auto()
    GIBBERISH = auto()

使用修飾過的 TokenSpec_ 函數，我們可以定義分詞器。我們使用 funcparserlib 中的 make_tokenizer 來建立一個採用 TokenSpec_ 定義清單的分詞器。每個定義指定一個標記類型（來自我們的規範枚舉）和一個與之相符的正規表示式。

from funcparserlib.lexer import TokenSpec

def TokenSpec_(spec: Spec, *args: Any, **kwargs: Any) -> TokenSpec:
    return TokenSpec(spec.name, *args, **kwargs)

OP正規表示式使用交替（|）來符合不同的函數格式。具體來說：

• mul(?=(d{1,3},d{1,3}))：僅當 mul 後面跟著包含兩個以逗號分隔的數字的括號時才符合 mul。正向先行斷言 (?=...) 確保括號和數字存在，但不會被匹配消耗。
• do(?=())：僅當後面跟有空括號時才符合。
• dont(?=())：僅當後面接空括號時才符合 don。

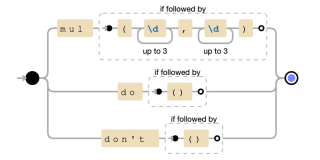
正規表示式的圖形表示

最後，tokenize 函數會在分詞過程中過濾掉任何亂碼標記，以專注於輸入的相關部分以進行進一步處理。

解釋程式碼的過程通常涉及兩個主要階段：詞法分析（或詞法分析）和解析。我們已經實現了第一階段：我們的 tokenize 函數充當詞法分析器，獲取輸入字串並將其轉換為標記序列。這些標記是解析器用來理解程式碼的結構和意義的基本建構塊。現在，讓我們探討一下解析器如何使用這些標記。

實作解析器

由 tokenize 函數傳回的已解析令牌隨後被傳送到解析器進行進一步處理。為了彌補 Spec Enum 和 tok 函數之間的差距，我們引入了一個名為 tok_ 的裝飾器。

from funcparserlib.lexer import make_tokenizer

def tokenize(input: str) -> tuple[Token, ...]:
    tokenizer = make_tokenizer(
        [
            TokenSpec_(
                Spec.OP, r"mul(?=\(\d{1,3},\d{1,3}\))|do(?=\(\))|don\'t(?=\(\))"
            ),
            TokenSpec_(Spec.NUMBER, r"\d{1,3}"),
            TokenSpec_(Spec.LPAREN, r"\("),
            TokenSpec_(Spec.RPAREN, r"\)"),
            TokenSpec_(Spec.COMMA, r","),
            TokenSpec_(Spec.GIBBERISH, r"[\s\S]"),
        ]
    )

    return tuple(
        token for token in tokenizer(input) if token.type != Spec.GIBBERISH.name
    )

例如，如果我們有一個 Spec.NUMBER 令牌，則傳回的解析器將接受該令牌，並傳回一個值，如下所示：

from funcparserlib.parser import tok

def tok_(spec: Spec, *args: Any, **kwargs: Any) -> Parser[Token, str]:
    return tok(spec.name, *args, **kwargs)

然後可以使用>>將傳回的值轉換為所需的資料類型。運算符，如下圖：

from enum import Enum, auto

class Spec(Enum):
    OP = auto()
    NUMBER = auto()
    COMMA = auto()
    LPAREN = auto()
    RPAREN = auto()
    GIBBERISH = auto()

通常，在解析未知輸入時最好使用 ast.literal_eval 以避免潛在的安全漏洞。然而，這個特定的「代​​碼降臨」謎題的限制（具體來說，所有數字都是有效整數）允許我們使用更直接、更有效率的 int 函數將字串表示形式轉換為整數。

from funcparserlib.lexer import TokenSpec

def TokenSpec_(spec: Spec, *args: Any, **kwargs: Any) -> TokenSpec:
    return TokenSpec(spec.name, *args, **kwargs)

我們可以定義解析規則來強制執行特定的標記序列並將其轉換為有意義的物件。例如，要解析 mul 函數調用，我們需要以下序列：左括號、數字、逗號、另一個數字、右括號。然後我們將此序列轉換為 Mul 物件：

from funcparserlib.lexer import make_tokenizer

def tokenize(input: str) -> tuple[Token, ...]:
    tokenizer = make_tokenizer(
        [
            TokenSpec_(
                Spec.OP, r"mul(?=\(\d{1,3},\d{1,3}\))|do(?=\(\))|don\'t(?=\(\))"
            ),
            TokenSpec_(Spec.NUMBER, r"\d{1,3}"),
            TokenSpec_(Spec.LPAREN, r"\("),
            TokenSpec_(Spec.RPAREN, r"\)"),
            TokenSpec_(Spec.COMMA, r","),
            TokenSpec_(Spec.GIBBERISH, r"[\s\S]"),
        ]
    )

    return tuple(
        token for token in tokenizer(input) if token.type != Spec.GIBBERISH.name
    )

此規則將所需標記（OP、LPAREN、COMMA、RPAREN）的 tok_ 解析器與數位解析器結合。 >>然後運算子將匹配的序列轉換為 Mul 對象，從索引 2 和 4 處的元組 elem 中提取兩個數字。

我們可以應用相同的原則來定義 do 和 don't 運算的解析規則。這些運算不帶參數（以空括號表示）並轉換為 Condition 物件：

from funcparserlib.parser import tok

def tok_(spec: Spec, *args: Any, **kwargs: Any) -> Parser[Token, str]:
    return tok(spec.name, *args, **kwargs)

do 規則建立一個 can_proceed = True 的 Condition 對象，而 don't 規則會建立一個 can_proceed = False 的 Condition 物件。

最後，我們使用 | 將這些單獨的解析規則（do、dont 和 mul）組合到單一 expr 解析器中。 （或）運算符：

>>> from funcparserlib.lexer import Token
>>> number_parser = tok_(Spec.NUMBER)
>>> number_parser.parse([Token(Spec.NUMBER.name, '123'])
'123'

此 expr 解析器將嘗試依序將輸入與每個規則進行匹配，傳回第一個成功匹配的結果。

我們的 expr 解析器可以處理完整的表達式，例如 mul(2,3)、do() 和 dont()。但是，輸入也可能包含不屬於這些結構化表達式的單獨標記。為了處理這些，我們定義了一個名為 everything 的包羅萬象的解析器：

>>> from funcparserlib.lexer import Token
>>> from ast import literal_eval
>>> number_parser = tok_(Spec.NUMBER) >> literal_eval
>>> number_parser.parse([Token(Spec.NUMBER.name, '123'])
123

這個解析器使用 | (或) 運算子來匹配 NUMBER、LPAREN、RPAREN 或 COMMA 類型的任何單一標記。它本質上是一種捕獲不屬於較大表達式的任何雜散標記的方法。

定義了所有元件後，我們現在可以定義完整程式的構成。程式由一個或多個「呼叫」組成，其中「呼叫」是可能被雜散標記包圍的表達式。

呼叫解析器處理此結構：它符合任意數量的雜散標記（許多（一切）），後面跟著單一表達式（expr），後面跟著任意數量的附加雜散標記。然後，operator.itemgetter(1) 函數從結果序列中提取匹配的表達式。

number = tok_(Spec.NUMBER) >> int

由程式解析器表示的完整程式由零個或多個呼叫組成，確保使用完成的解析器消耗整個輸入。然後將解析結果轉換為表達式元組。

from enum import Enum, auto

class Spec(Enum):
    OP = auto()
    NUMBER = auto()
    COMMA = auto()
    LPAREN = auto()
    RPAREN = auto()
    GIBBERISH = auto()

最後，我們將所有這些定義分組到一個解析函數中。此函數將標記元組作為輸入並傳回已解析表達式的元組。所有解析器都在函數體內定義，以防止污染全域命名空間，並且因為數字解析器依賴 tok_ 函數。

from funcparserlib.lexer import TokenSpec

def TokenSpec_(spec: Spec, *args: Any, **kwargs: Any) -> TokenSpec:
    return TokenSpec(spec.name, *args, **kwargs)

解決難題

有了我們的解析器，解決第 1 部分就很簡單了。我們需要找到所有乘法運算，執行乘法並對結果求和。我們先定義一個處理 Mul 表達式的評估函數

from funcparserlib.lexer import make_tokenizer

def tokenize(input: str) -> tuple[Token, ...]:
    tokenizer = make_tokenizer(
        [
            TokenSpec_(
                Spec.OP, r"mul(?=\(\d{1,3},\d{1,3}\))|do(?=\(\))|don\'t(?=\(\))"
            ),
            TokenSpec_(Spec.NUMBER, r"\d{1,3}"),
            TokenSpec_(Spec.LPAREN, r"\("),
            TokenSpec_(Spec.RPAREN, r"\)"),
            TokenSpec_(Spec.COMMA, r","),
            TokenSpec_(Spec.GIBBERISH, r"[\s\S]"),
        ]
    )

    return tuple(
        token for token in tokenizer(input) if token.type != Spec.GIBBERISH.name
    )

為了解決第 1 部分，我們對輸入進行標記和解析，然後使用我們剛剛定義的函數評估_skip_condition 來獲得最終結果：

from funcparserlib.parser import tok

def tok_(spec: Spec, *args: Any, **kwargs: Any) -> Parser[Token, str]:
    return tok(spec.name, *args, **kwargs)

對於第 2 部分，如果遇到不條件，我們需要跳過計算 mul 操作。我們定義一個新的評估函數，evaluate_with_condition，來處理這個問題：

>>> from funcparserlib.lexer import Token
>>> number_parser = tok_(Spec.NUMBER)
>>> number_parser.parse([Token(Spec.NUMBER.name, '123'])
'123'

函數使用reduce和自訂reducer函數來維護運行總和和布林標誌（條件）。當遇到條件表達式（do 或 don）時，條件標誌會更新。只有當條件為 True 時，才會計算 Mul 表達式並將其加到總和中。

上一次迭代

最初，我的解析方法涉及兩個不同的過程。首先，我將對整個輸入字串進行標記，收集所有標記，無論其類型為何。然後，在一個單獨的步驟中，我將專門執行第二次標記化和解析，以識別和處理 mul 操作。

>>> from funcparserlib.lexer import Token
>>> from ast import literal_eval
>>> number_parser = tok_(Spec.NUMBER) >> literal_eval
>>> number_parser.parse([Token(Spec.NUMBER.name, '123'])
123

改進的方法透過在一次傳遞中執行標記化和解析來消除這種冗餘。我們現在有一個解析器可以處理所有標記類型，包括與 mul、do、dont 和其他單獨標記相關的標記類型。

number = tok_(Spec.NUMBER) >> int

我們沒有重新標記輸入來找出 mul 操作，而是利用初始標記化過程中辨識的標記類型。解析函數現在使用這些標記類型來直接建構適當的表達式物件（Mul、Condition 等）。這樣就避免了輸入的冗餘掃描，顯著提高了效率。

本週「程式碼降臨」的解析之旅就到此結束了。雖然這篇文章需要大量的時間投入，但重新審視和鞏固我的詞法分析和解析知識的過程使其成為一項值得的努力。這是一個有趣且富有洞察力的謎題，我渴望在未來幾週內應對更複雜的挑戰並分享我的經驗。

一如既往，感謝您的閱讀，下週我會再寫信。

以上是如何解析電腦程式碼，程式碼的出現 ay 3的詳細內容。更多資訊請關注PHP中文網其他相關文章！