理解 JavaScript 中的大 O 表示法和時間複雜度

使用 JavaScript 時，編寫函數式程式碼很重要，但確保其高效運作也同樣重要。這就是 Big O 表示法的用武之地。它提供了一種方法來分析程式碼的效能如何隨著輸入大小的增加而擴展，從而幫助您編寫最佳化且可擴展的應用程式。

本文將透過 JavaScript 中適合初學者的範例來探索 Big O 表示法和常見時間複雜度的基礎知識

什麼是大 O 表示法？

大O表示法是描述演算法效率的數學表示形式。它幫助我們理解：

1. 時間複雜度：演算法的執行時間如何隨輸入大小的變化而改變。
2. 空間複雜度：演算法的記憶體使用量如何隨輸入大小的變化而變化。

目標是評估演算法隨著輸入大小的增長而表現如何，並專注於最壞的情況。

---

為什麼大 O 表示法很重要？

假設您的任務是在電話簿中找出姓名：

• 一種方法是翻閱每一頁，直到找到名稱（線性搜尋）。
• 另一種是從中間開始，有系統地縮小範圍（二分查找）。

兩種方法都可以解決問題，但是隨著電話簿大小的增長，它們的效率差異很大。 Big O 幫助我們比較這些方法並選擇最好的方法。

---

大 O 表示法的實際應用

以下是常見的 Big O 複雜性，並透過 JavaScript 中的實際範例進行了解釋。

---

1. O(1) - 恆定時間

無論輸入大小為何，運轉時間都保持不變。這些操作是最有效率的。

範例：透過索引存取陣列中的元素。

const numbers = [10, 20, 30, 40, 50];
console.log(numbers[2]); // Always takes the same time, no matter the array size

---

2. O(log n) - 對數時間

隨著輸入大小的增加，運行時間呈對數增長。這通常發生在二分搜尋等分治演算法中。

範例： 對排序數組進行二分搜尋。

function binarySearch(arr, target) {
    let start = 0;
    let end = arr.length - 1;

    while (start <= end) {
        const mid = Math.floor((start + end) / 2);

        if (arr[mid] === target) {
            return mid;
        } else if (arr[mid] < target) {
            start = mid + 1; // Search the right half
        } else {
            end = mid - 1; // Search the left half
        }
    }

    return -1; // Target not found
}

const arr = [1, 3, 5, 7, 9];
console.log(binarySearch(arr, 7)); // Output: 3

---

3. O(n) - 線性時間

運行時間與輸入大小成比例增長。當您需要檢查每個元素一次時，就會發生這種情況。

範例：在未排序的陣列中尋找項目。

function linearSearch(arr, target) {
    for (let i = 0; i < arr.length; i++) {
        if (arr[i] === target) {
            return i; // Found
        }
    }
    return -1; // Not found
}

const items = [10, 20, 30, 40, 50];
console.log(linearSearch(items, 30)); // Output: 2

---

4. O(n²) - 二次時間

隨著輸入大小的增加，運行時間呈現二次方成長。這在具有嵌套循環的演算法中是典型的。

範例：基本的冒泡排序實作。

const numbers = [10, 20, 30, 40, 50];
console.log(numbers[2]); // Always takes the same time, no matter the array size

---

5. O(2ⁿ) - 指數時間

每增加一個輸入，運行時間就會加倍。這種情況發生在遞歸解決問題的演算法中，考慮所有可能的解決方案。

範例：遞歸計算斐波那契數。

function binarySearch(arr, target) {
    let start = 0;
    let end = arr.length - 1;

    while (start <= end) {
        const mid = Math.floor((start + end) / 2);

        if (arr[mid] === target) {
            return mid;
        } else if (arr[mid] < target) {
            start = mid + 1; // Search the right half
        } else {
            end = mid - 1; // Search the left half
        }
    }

    return -1; // Target not found
}

const arr = [1, 3, 5, 7, 9];
console.log(binarySearch(arr, 7)); // Output: 3

---

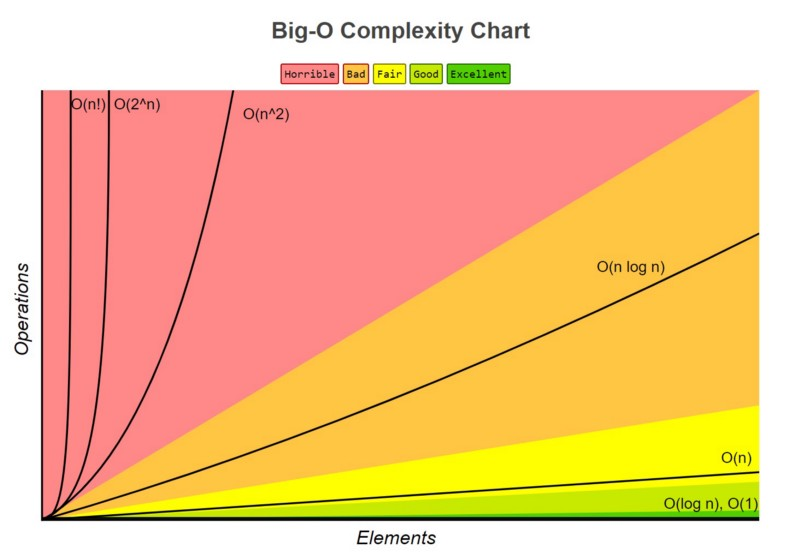
可視化大O

以下是隨著輸入大小的增加，不同 Big O 複雜度的比較：

Big O	Name	Example Use Case	Growth Rate
O(1)	Constant	Array access	Flat
O(log n)	Logarithmic	Binary search	Slow growth
O(n)	Linear	Looping through an array	Moderate growth
O(n²)	Quadratic	Nested loops	Rapid growth
O(2ⁿ)	Exponential	Recursive brute force	Very fast growth

---

成長率說明

想像一下您正在解決一個問題，並且輸入大小增加。以下是不同複雜度的演算法如何隨著輸入大小的增加而擴展：

Input Size	O(1)	O(log n)	O(n)	O(n²)	O(2ⁿ)
1	1 ms	1 ms	1 ms	1 ms	1 ms
10	1 ms	3 ms	10 ms	100 ms	~1 sec
100	1 ms	7 ms	100 ms	10 sec	~centuries
1000	1 ms	10 ms	1 sec	~17 min	Unrealistic

• O(1) 無論輸入如何，都保持不變。
• O(log n) 成長緩慢，非常適合大輸入。
• O(n) 與輸入大小成比例成長。
• O(n²) 及更高的值對於大輸入很快變得不切實際。

---

用代碼可視化 Big O

以下是如何使用簡單的計數器來視覺化不同複雜度的操作數量：

const numbers = [10, 20, 30, 40, 50];
console.log(numbers[2]); // Always takes the same time, no matter the array size

---

關於 Big O 的常見誤解

1. Big O ≠ 實際表現：Big O 告訴您表現如何衡量，而不是所花費的確切時間。
   • 例如，對於小輸入大小，具有較小常數因子的 O(n) 演算法可能優於 O(log n) 演算法。
2. 最佳情況與最壞情況：Big O 通常描述最壞的情況。例如，搜尋不在清單中的項目。
3. 並非所有巢狀循環都是 O(n²)：複雜性取決於內循環處理的元素數量。

---

初學者實用技巧

1. 專注於 O(1)、O(n) 和 O(n²)：這些是您會遇到的最常見的複雜性。
2. 衡量效能：使用 Chrome DevTools 等工具對您的程式碼進行基準測試。
3. 重構以提高效率：程式碼運行後，識別複雜性較高的部分並進行最佳化。
4. 不斷學習：LeetCode 和 HackerRank 等平台為理解 Big O 提供了很好的練習。

---

結論

大 O 表示法是評估演算法效率和了解程式碼擴充方式的重要工具。透過掌握基礎知識並分析常見模式，您將能夠很好地編寫高效能的 JavaScript 應用程式。

編碼愉快！ ？

以上是理解 JavaScript 中的大 O 表示法和時間複雜度的詳細內容。更多資訊請關注PHP中文網其他相關文章！