反應模型解釋
前言
自從我開始開發應用程式和網站以來已經過去了 10 年,但 JavaScript 生態系統從未像今天這樣令人興奮!
2022 年,社群被「訊號」的概念所吸引,以至於大多數 JavaScript 框架都將它們整合到自己的引擎中。我正在考慮 Preact,它自 2022 年 9 月以來提供了與組件生命週期分離的反應變量;或者最近的 Angular,它於 2023 年 5 月實驗性地實現了 Signals,然後從版本 18 正式開始。其他 JavaScript 函式庫也選擇重新考慮他們的方法...
從 2023 年到現在,我一直在各個專案中使用 Signals。它們的實施和使用簡單性完全說服了我,以至於我在技術研討會、培訓課程和會議期間與我的專業網絡分享了它們的好處。
但最近,我開始問自己這個概念是否真正具有「革命性」/是否有訊號的替代品?因此,我更深入地研究了這種反思,並發現了反應式系統的不同方法。
這篇文章概述了不同的反應模型,以及我對它們如何運作的理解。
注意: 說到這裡,你可能已經猜到了,我不會討論Java 的「Reactive Streams」;否則,我會把這篇文章的標題定為「背壓是什麼鬼! 理論
當我們談論反應性模型時,我們(首先也是最重要的)談論“
反應性程式”,但特別是“反應性”。
響應式程式設計是一種開發範例,允許將資料來源的變更自動傳播給消費者。 因此,我們可以將
反應性定義為根據資料的變化即時更新依賴關係的能力。
NB:簡而言之,當使用者填寫和/或提交表單時,我們必須對這些變更做出反應,顯示載入元件或任何其他指定正在發生的事情。 .. 另一個例子,當非同步接收資料時,我們必須透過顯示全部或部分資料、執行新操作等來做出反應 在這種情況下,反應式函式庫提供了自動更新和高效傳播的變量,使編寫簡單且最佳化的程式碼變得更加容易。
為了提高效率,當且僅當它們的值發生變化時,這些系統必須重新計算/重新評估這些變數!同樣,為了確保廣播的數據保持一致和最新,系統必須避免顯示任何中間狀態(特別是在狀態變化的計算期間)。
NB:狀態是指程式/應用程式整個生命週期中使用的資料/值。
好吧,但是…這些「反應模型」到底是什麼?
PUSH,又稱為「急切」反應
第一個反應模型稱為「PUSH」(或「渴望」反應)。本系統基於以下原則:
- 資料來源的初始化(稱為「Observables」)
- 元件/函數訂閱這些資料來源(這些是消費者)
- 當數值改變時,資料會立即傳播給消費者(稱為「觀察者」)
如您可能已經猜到的,「PUSH」模型依賴「Observable/Observer」設計模式。
第一個用例:初始狀態和狀態更改
讓我們考慮以下初始狀態,
let a = { firstName: "John", lastName: "Doe" };
const b = a.firstName;
const c = a.lastName;
const d = `${b} ${c}`;

使用反應式函式庫(例如 RxJS),這個初始狀態看起來比較像這樣:
let a = observable.of({ firstName: "John", lastName: "Doe" });
const b = a.pipe(map((a) => a.firstName));
const c = a.pipe(map((a) => a.lastName));
const d = merge(b, c).pipe(reduce((b, c) => `${b} ${c}`));
注意:為了這篇文章的目的,所有程式碼片段都應被視為「偽代碼」。
現在,我們假設消費者(例如元件)希望在資料來源更新時記錄狀態 D 的值,
d.subscribe((value) => console.log(value));
我們的元件將訂閱資料流;它仍然需要觸發改變,
a.next({ firstName: "Jane", lastName: "Doe" });
從那裡,「PUSH」系統偵測到變更並自動將其廣播給消費者。基於上面的初始狀態,以下是可能發生的操作的描述:
- 資料來源A發生狀態變化!
- A的值傳播到B(資料來源B的計算);
- 然後,將B的值傳播到D(資料來源D的計算);
- A的值傳播到C(資料來源C的計算);
- 最後將C的值傳播到D(資料來源D的重新計算);

該系統的挑戰之一在於計算順序。事實上,根據我們的用例,您會注意到 D 可能會被評估兩次:第一次使用 C 的先前狀態值;第二次使用 C 的值。第二次,C 的值是最新的!在這個反應模型中,這個挑戰被稱為「鑽石問題」 ️。
第二個用例:下一次迭代
現在,我們假設該狀態依賴兩個主要資料來源,
let a = { firstName: "John", lastName: "Doe" };
const b = a.firstName;
const c = a.lastName;
const d = `${b} ${c}`;
更新 E 時,系統將重新計算整個狀態,這使得系統可以透過覆蓋先前的狀態來保留單一事實來源。
- 資料來源E發生狀態變化!
- A的值傳播到B(資料來源B的計算);
- 然後,將B的值傳播到D(資料來源D的計算);
- A的值傳播到C(資料來源C的計算);
- E的值傳播到C(資料來源C的重新計算);.
- 最後將C的值傳播到D(資料來源D的重新計算);

「鑽石問題」再次發生...這次是在資料來源 C 上,可能會評估 2 次,並且始終在 D 上。
鑽石問題
「鑽石問題」並不是「渴望」反應模型中的新挑戰。一些計算演算法(尤其是 MobX 使用的演算法)可以標記「反應式依賴樹的節點」以平衡狀態計算。透過這種方法,系統將首先評估「根」資料來源(在我們的範例中為 A 和 E),然後是 B 和 C,最後是 D。更改狀態計算的順序有助於解決此類問題。

PULL,又稱「惰性」反應
第二個反應模型稱為「PULL」。與“PUSH”模型不同,它基於以下原則:
- 反應變數的宣告
- 系統延遲狀態計算
- 派生狀態是根據其依賴關係計算的
- 系統避免過度更新
最重要的是要記住最後一條規則:與先前的系統不同,最後一條規則推遲了狀態計算,以避免對相同資料來源進行多次評估。
第一個用例:初始狀態和狀態更改
讓我們保持之前的初始狀態...

在這種系統中,初始狀態語法將採用以下形式:
let a = observable.of({ firstName: "John", lastName: "Doe" });
const b = a.pipe(map((a) => a.firstName));
const c = a.pipe(map((a) => a.lastName));
const d = merge(b, c).pipe(reduce((b, c) => `${b} ${c}`));
注意: React 愛好者可能會認識這個文法 ?
宣告一個反應變數給一個元組「誕生」:一方面是不可變的變數;另一個變數的更新函數。其餘語句(在我們的例子中為 B、C 和 D)被視為派生狀態,因為它們「監聽」各自的依賴關係。
d.subscribe((value) => console.log(value));
「惰性」系統的定義特徵是它不會立即傳播更改,而是僅在明確請求時傳播更改。
let a = { firstName: "John", lastName: "Doe" };
const b = a.firstName;
const c = a.lastName;
const d = `${b} ${c}`;
在「PULL」模型中,使用effect()(來自組件)來記錄反應變數(指定為依賴項)的值會觸發狀態變更的計算:
- D 將檢查其依賴項(B 和 C)是否已更新;
- B 將檢查其依賴項 (A) 是否已更新;
- A 將其值傳播給 B(計算 B 的值);
- C 將檢查其相依性 (A) 是否已更新;
- A 會將其值傳播給 C(計算 C 的值)
- B和C將各自的值傳播給D(計算D的值);

在查詢依賴項時可以最佳化此系統。事實上,在上面的場景中,A 被查詢了兩次以確定它是否已更新。但是,第一個查詢可能足以定義狀態是否已變更。 C 不需要執行此操作...相反,A 只能廣播其值。
第二個用例:下一次迭代
讓我們透過加入第二個反應變數「root」來讓狀態稍微複雜一些,
let a = observable.of({ firstName: "John", lastName: "Doe" });
const b = a.pipe(map((a) => a.firstName));
const c = a.pipe(map((a) => a.lastName));
const d = merge(b, c).pipe(reduce((b, c) => `${b} ${c}`));
系統再次延遲狀態計算,直到明確要求為止。使用與之前相同的效果,更新新的反應變數將觸發以下步驟:
- D 將檢查其依賴項(B 和 C)是否已更新;
- B 將檢查其依賴項 (A) 是否已更新;
- C 將檢查其依賴項(A 和 E)是否已更新;
- E 將其值傳播給 C,C 將透過記憶取得 A 的值(計算 C 的值);
- C 將其值傳播給 D,D 將透過記憶取得 B 的值(計算 D 的值);

由於 A 的值沒有改變,所以不需要重新計算這個變數(同樣的情況也適用於 B 的值)。在這種情況下,使用記憶演算法可以提高狀態計算期間的表現。
推拉,又稱「細粒度」反應
最後一個反應模型是「推拉」系統。術語「PUSH」反映了更改通知的立即傳播,而「PULL」指的是按需獲取狀態值。這種方法與所謂的「細粒度」反應性密切相關,它遵循以下原則:
- 反應變數的聲明(我們談論的是反應基元)
- 在原子層級追蹤依賴關係
- 變更傳播具有高度針對性
請注意,這種反應性並非「推拉」模型所獨有。細粒度反應性是指對系統依賴性的精確追蹤。因此,還有 PUSH 和 PULL 反應模型也以這種方式工作(我正在考慮 Jotai 或 Recoil。
第一個用例:初始狀態和狀態更改
仍基於先前的初始狀態...「細粒度」反應系統中初始狀態的聲明如下所示:
let a = { firstName: "John", lastName: "Doe" };
const b = a.firstName;
const c = a.lastName;
const d = `${b} ${c}`;
注意:signal關鍵字的使用不只是軼事?
在語法方面,它與「PUSH」模型非常相似,但有一個顯著且重要的區別:依賴關係! 在「細粒度」反應系統中,沒有必要明確聲明計算派生狀態所需的依賴關係,因為這些狀態隱式追蹤它們使用的變數。在我們的例子中,B 和 C 將自動追蹤 A 值的更改,D 將追蹤 B 和 C 的更改。
let a = observable.of({ firstName: "John", lastName: "Doe" });
const b = a.pipe(map((a) => a.firstName));
const c = a.pipe(map((a) => a.lastName));
const d = merge(b, c).pipe(reduce((b, c) => `${b} ${c}`));
在這樣的系統中,更新反應變數比基本的「PUSH」模型更有效,因為變更會自動傳播到依賴它的衍生變數(僅作為通知,而不是值本身) 。
d.subscribe((value) => console.log(value));
然後,根據需要(讓我們以logger 為例),系統內使用D 將取得關聯根狀態的值(在我們的例子中為A),計算值導出狀態( B和C),最後評估D。這不是一個直覺的操作方式嗎?

第二個用例:下一次迭代
讓我們考慮以下狀態,
a.next({ firstName: "Jane", lastName: "Doe" });
再一次,推拉系統的「細粒度」方面允許自動追蹤每個狀態。因此,派生狀態 C 現在追蹤根狀態 A 和 E。更新變數 E 將觸發以下操作:
- 反應原語 E 的狀態變化!
- 目標變更通知(透過 C 從 E 到 D);
- E將其值傳播給C,C將透過記憶檢索A的值(計算C的值);
- C 會將其值傳播給 D,D 將透過 memoization 檢索 B 的值(計算 D 的值);

這是反應性依賴關係相互之間的先前關聯,使得模型如此有效率!
確實,在經典的「PULL」系統(例如React 的Virtual DOM)中,當從元件更新響應式狀態時,框架將收到變更通知(觸發「 差異”階段)。然後,根據需要(和延遲),框架將通過遍歷反應式依賴樹來計算更改;每次更新變數時!這種對依賴狀態的「發現」需要付出巨大的代價......
透過「細粒度」反應性系統(如訊號),反應性變數/基元的更新會自動通知與它們相關的任何派生狀態的變化。因此,無需(重新)發現關聯的依賴關係;狀態傳播是有針對性的!
結論(.值)
到 2024 年,大多數 Web 框架都選擇重新思考它們的工作方式,特別是在反應性模型方面。這種轉變總體上提高了他們的效率和競爭力。其他人選擇(仍然)混合(我在這裡考慮的是 Vue),這使他們在許多情況下更加靈活。
最後,無論選擇什麼模型,在我看來,一個(好的)反應式系統是建立在一些主要規則之上的:
- 系統防止不一致的衍生狀態;
- 在系統中使用狀態會導致反應式派生狀態;
- 系統盡量減少過多的工作;
- 並且,「對於給定的初始狀態,無論狀態遵循的路徑,系統的最終結果將始終相同!」
最後一點可以解釋為聲明式程式設計的基本原則,這就是我如何看待(好的)反應式系統需要確定性!這就是使反應式模型可靠、可預測且易於在大規模技術專案中使用的“決定論”,無論演算法有多複雜。
以上是反應性是什麼鬼! ?的詳細內容。更多資訊請關注PHP中文網其他相關文章!
 在JavaScript中替換字符串字符Mar 11, 2025 am 12:07 AM
在JavaScript中替換字符串字符Mar 11, 2025 am 12:07 AMJavaScript字符串替換方法詳解及常見問題解答 本文將探討兩種在JavaScript中替換字符串字符的方法:在JavaScript代碼內部替換和在網頁HTML內部替換。 在JavaScript代碼內部替換字符串 最直接的方法是使用replace()方法: str = str.replace("find","replace"); 該方法僅替換第一個匹配項。要替換所有匹配項,需使用正則表達式並添加全局標誌g: str = str.replace(/fi
 構建您自己的Ajax Web應用程序Mar 09, 2025 am 12:11 AM
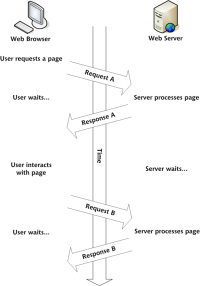
構建您自己的Ajax Web應用程序Mar 09, 2025 am 12:11 AM因此,在這裡,您準備好了解所有稱為Ajax的東西。但是,到底是什麼? AJAX一詞是指用於創建動態,交互式Web內容的一系列寬鬆的技術。 Ajax一詞,最初由Jesse J創造
 如何在瀏覽器中優化JavaScript代碼以進行性能?Mar 18, 2025 pm 03:14 PM
如何在瀏覽器中優化JavaScript代碼以進行性能?Mar 18, 2025 pm 03:14 PM本文討論了在瀏覽器中優化JavaScript性能的策略,重點是減少執行時間並最大程度地減少對頁面負載速度的影響。
 如何使用瀏覽器開發人員工具有效調試JavaScript代碼?Mar 18, 2025 pm 03:16 PM
如何使用瀏覽器開發人員工具有效調試JavaScript代碼?Mar 18, 2025 pm 03:16 PM本文討論了使用瀏覽器開發人員工具的有效JavaScript調試,專注於設置斷點,使用控制台和分析性能。
 jQuery矩陣效果Mar 10, 2025 am 12:52 AM
jQuery矩陣效果Mar 10, 2025 am 12:52 AM將矩陣電影特效帶入你的網頁!這是一個基於著名電影《黑客帝國》的酷炫jQuery插件。該插件模擬了電影中經典的綠色字符特效,只需選擇一張圖片,插件就會將其轉換為充滿數字字符的矩陣風格畫面。快來試試吧,非常有趣! 工作原理 插件將圖片加載到畫布上,讀取像素和顏色值: data = ctx.getImageData(x, y, settings.grainSize, settings.grainSize).data 插件巧妙地讀取圖片的矩形區域,並利用jQuery計算每個區域的平均顏色。然後,使用
 如何構建簡單的jQuery滑塊Mar 11, 2025 am 12:19 AM
如何構建簡單的jQuery滑塊Mar 11, 2025 am 12:19 AM本文將引導您使用jQuery庫創建一個簡單的圖片輪播。我們將使用bxSlider庫,它基於jQuery構建,並提供許多配置選項來設置輪播。 如今,圖片輪播已成為網站必備功能——一圖胜千言! 決定使用圖片輪播後,下一個問題是如何創建它。首先,您需要收集高質量、高分辨率的圖片。 接下來,您需要使用HTML和一些JavaScript代碼來創建圖片輪播。網絡上有很多庫可以幫助您以不同的方式創建輪播。我們將使用開源的bxSlider庫。 bxSlider庫支持響應式設計,因此使用此庫構建的輪播可以適應任何
 如何使用Angular上傳和下載CSV文件Mar 10, 2025 am 01:01 AM
如何使用Angular上傳和下載CSV文件Mar 10, 2025 am 01:01 AM數據集對於構建API模型和各種業務流程至關重要。這就是為什麼導入和導出CSV是經常需要的功能。在本教程中,您將學習如何在Angular中下載和導入CSV文件


熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

WebStorm Mac版
好用的JavaScript開發工具

mPDF
mPDF是一個PHP庫,可以從UTF-8編碼的HTML產生PDF檔案。原作者Ian Back編寫mPDF以從他的網站上「即時」輸出PDF文件,並處理不同的語言。與原始腳本如HTML2FPDF相比,它的速度較慢,並且在使用Unicode字體時產生的檔案較大,但支援CSS樣式等,並進行了大量增強。支援幾乎所有語言,包括RTL(阿拉伯語和希伯來語)和CJK(中日韓)。支援嵌套的區塊級元素(如P、DIV),

Dreamweaver CS6
視覺化網頁開發工具

PhpStorm Mac 版本
最新(2018.2.1 )專業的PHP整合開發工具

MinGW - Minimalist GNU for Windows
這個專案正在遷移到osdn.net/projects/mingw的過程中,你可以繼續在那裡關注我們。 MinGW:GNU編譯器集合(GCC)的本機Windows移植版本,可自由分發的導入函式庫和用於建置本機Windows應用程式的頭檔;包括對MSVC執行時間的擴展,以支援C99功能。 MinGW的所有軟體都可以在64位元Windows平台上運作。







