研究 np.einsum 的性能

我上一篇博文的一位讀者向我指出，對於切片matmul 之類的操作，np.einsum 比np.matmul 慢得多，除非您在參數列表中打開優化標誌： np.einsum(. . ., 最佳化= True).

帶著一些懷疑，我啟動了 Jupyter 筆記本並做了一些初步測試。 我天哪，這是完全正確的 - 即使對於兩個操作數的情況，優化根本不應該產生任何區別！

檢定 1 非常簡單 - 兩個不同維度的 C 階（又稱行主階）矩陣的矩陣乘法。 np.matmul 總是快二十倍左右。

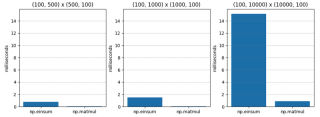
M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	0.765	0.045	17.055
(100, 1000)	(1000, 100)	1.495	0.073	20.554
(100, 10000)	(10000, 100)	15.148	0.896	16.899

對於檢定2，當optimize=True時，結果截然不同。 np.einsum 仍然較慢，但最壞情況下僅慢 1.5 倍左右！

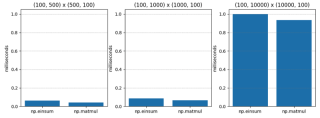
M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	0.063	0.043	1.474
(100, 1000)	(1000, 100)	0.086	0.067	1.284
(100, 10000)	(10000, 100)	1.000	0.936	1.068

為什麼？

我對最佳化標誌的理解是，當存在三個或更多操作數時，它確定最佳收縮順序。 這裡，我們只有兩個操作數。 所以優化應該不會有什麼不同，對吧？

但也許優化不只是選擇收縮順序？ 也許優化器知道記憶體佈局，這與行優先與列優先佈局有關？

在矩陣乘法的小學方法中，要計算單個條目，您將迭代op1 中的行，同時迭代op2 中的列，因此將第二個參數按列優先順序放置可能會導致加速對於np.einsum （假設np.einsum 有點像是底層矩陣乘法的小學方法的通用版本，我懷疑這是真的）。

因此，對於 測試 3，我為第二個運算元傳遞了一個列主矩陣，以查看當 optimize=False 時這是否會加快 np.einsum 的速度。

這是結果。 令人驚訝的是，np.einsum 還是相當更糟。 顯然，發生了一些我不明白的事情 - 當 optimize 為 True 時，也許 np.einsum 使用完全不同的程式碼路徑？ 是時候開始挖掘了。

M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	1.486	0.056	26.541
(100, 1000)	(1000, 100)	3.885	0.125	31.070
(100, 10000)	(10000, 100)	49.669	1.047	47.444

更深入

Numpy 1.12.0 的發行說明提到了最佳化標誌的引入。 然而，優化的目的似乎是確定操作數鏈中參數的組合順序（即關聯性） - 因此優化不應僅對兩個操作數產生影響，對吧？ 以下是發行說明：

np.einsum 現在支援最佳化參數，它將最佳化收縮順序。例如，np.einsum 將在一次傳遞中完成鏈點範例np.einsum('ij,jk,kl->il', a, b, c)，其縮放比例類似於N^4；然而，當optimize= True時，np.einsum將建立一個中間數組，以將此縮放減少到N^3或有效地np.dot(a, b).dot(c)。使用中間張量來減少縮放已應用於通用 einsum 求和符號。有關更多詳細信息，請參閱 np.einsum_path。

為了讓這個謎團更加複雜，一些後來的發行說明表明 np.einsum 已升級為使用tensordot（它本身在適當的情況下使用BLAS）。 現在，這似乎很有希望。

但是，為什麼我們只在最佳化為True時看到加速？ 發生什麼事了？

如果我們在numpy/numpy/_core/einsumfunc.py 中閱讀def einsum(*operands, out=None, optimization=False, **kwargs) ，我們幾乎會立即看到這個提前退出的邏輯：

c_einsum 是否使用tensordot？ 我對此表示懷疑。 稍後在程式碼中，我們看到 1.14 註解似乎引用了 tensordot 呼叫：

所以，這就是發生的事情：

1. 如果 optimization 為 True，則收縮清單循環將被執行 - 即使在簡單的兩個操作數情況下也是如此。
2. tensordot僅在收縮_列表循環中呼叫。
3. 因此，當optimize為True時，我們呼叫tensordot（因此也呼叫BLAS）。

對我來說，這似乎是個錯誤。 恕我直言， np.einsum 開頭的「提前退出」仍應偵測運算元是否與tensordot相容，並在可能的情況下呼叫tensordot。 然後，即使優化為 False，我們也會得到明顯的 BLAS 加速。 畢竟，最佳化的語義與收縮順序有關，而不是與 BLAS 的使用有關，我認為這應該是給定的。

這裡的好處是，調用 np.einsum 進行相當於張量調用的操作的人將獲得適當的加速，從性能角度來看，這使得 np.einsum 的危險性降低了一些。

c_einsum 實際上是如何運作的？

我深入研究了一些 C 程式碼來檢查它。 實現的核心就在這裡。

經過大量的參數解析和參數準備，確定了軸迭代順序並準備了專用迭代器。 迭代器的每個收益都代表了同時跨越所有操作數的不同方式。

假設某些特殊情況最佳化不適用，則根據涉及的資料類型確定適當的乘積和 (sop) 函數：

然後，在從迭代器返回的每個多操作數步幅上呼叫此乘積和 (sop) 運算，如下所示：

這就是我對 einsum 工作原理的理解，誠然，它仍然有點薄弱——它確實值得我花更多的時間來了解它。

但它確實證實了我的懷疑，它的作用就像小學矩陣乘法方法的廣義、千兆腦版本。 最終，它委託給一系列「乘積之和」運算，這些運算依賴於在操作數中移動的「跨步器」——與學習矩陣乘法時用手指所做的沒有太大不同。

概括

那為什麼當你使用optimize=True呼叫np.einsum時通常會比較快呢？ 原因有兩個。

第一個（也是最初的）原因是它試圖找到最佳的收縮路徑。 然而，正如我所指出的，當我們只有兩個操作數時，這應該不重要，就像我們在效能測試中所做的那樣。

第二個（也是較新的）原因是，當optimize=True時，即使在兩個運算元的情況下，它也會啟動一個程式碼路徑，在可能的情況下呼叫tensordot，而tensordot又會嘗試使用BLAS。 BLAS 與矩陣乘法一樣最佳化！

所以，雙重操作數加速之謎解決了！ 然而，我們還沒有真正涵蓋由於收縮順序而導致的加速特性。 這得等以後的貼文了！ 敬請期待！

以上是研究 np.einsum 的性能的詳細內容。更多資訊請關注PHP中文網其他相關文章！