numpy&#s einsum 的不合理用處

介紹

我想向您介紹Python中最有用的方法，np.einsum。

使用 np.einsum（以及 Tensorflow 和 JAX 中的對應項），您可以以極其清晰和簡潔的方式編寫複雜的矩陣和張量運算。 我還發現它的清晰性和簡潔性減輕了許多使用張量帶來的精神負擔。

而且它實際上學習和使用起來相當簡單。 其工作原理如下：

在 np.einsum 中，您有一個下標字串參數，並且有一個或多個運算元：

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

下標參數是一種“迷你語言”，它告訴 numpy 如何操作和組合運算元的軸。 剛開始讀起來有點困難，但是掌握訣竅後也不錯。

單一操作數

第一個範例，讓我們使用 np.einsum 交換矩陣 A 的軸（也稱為轉置）：

M = np.einsum('ij->ji', A)

字母 i 和 j 綁定到 A 的第一個和第二個軸。 Numpy 按照字母出現的順序將字母綁定到軸，但如果你是顯式的，numpy 並不在乎你使用什麼字母。 例如，我們可以使用 a 和 b，其工作方式相同：

M = np.einsum('ab->ba', A)

但是，您必須提供與操作數中的軸一樣多的字母。 A 中有兩個軸，因此您必須提供兩個不同的字母。 下一個範例不會工作，因為下標公式只有一個字母要綁定，i：

# broken
M = np.einsum('i->i', A)

另一方面，如果操作數確實只有一個軸（即，它是一個向量），那麼單字母下標公式就可以正常工作，儘管它不是很有用，因為它使向量成為原樣：

m = np.einsum('i->i', a)

對軸求和

但是這個操作呢？ 右邊沒有 i。 這有效嗎？

c = np.einsum('i->', a)

令人驚訝的是，是的！

這是理解 np.einsum 本質的第一個關鍵：如果一個軸從右側省略，那麼該軸對求和。

代碼：

c = 0
I = len(a)
for i in range(I):
   c += a[i]

求和行為不限於單一軸。 例如，您可以使用下列下標公式同時對兩個軸求和： c = np.einsum('ij->', A):

這是兩個軸上對應的 Python 程式碼：

c = 0
I,J = A.shape
for i in range(I):
   for j in range(J):
      c += A[i,j]

但它不止於此 - 我們可以發揮創造力，對一些軸進行求和，而忽略其他軸。 例如： np.einsum('ij->i', A) 對矩陣 A 的行求和，留下長度為 j 的行和向量：

代碼：

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

同樣，np.einsum('ij->j', A) 對 A 中的列進行求和。

代碼：

M = np.einsum('ij->ji', A)

兩個操作數

我們用單一運算元可以做的事情是有限的。 使用兩個操作數，事情會變得更加有趣（並且有用）。

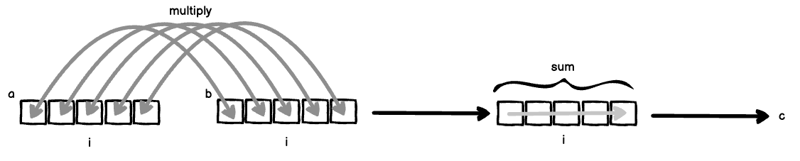
假設您有兩個向量 a = [a_1, a_2, ... ] 和 b = [a_1, a_2, ...]。

如果 len(a) === len(b)，我們可以這樣計算內積（也稱為點積）：

M = np.einsum('ab->ba', A)

這裡同時發生兩件事：

1. 因為 i 與 a 和 b 都綁定，所以 a 和 b 會「排列」然後相乘：a[i] * b[i]。
2. 因為索引 i 被排除在右側，所以對軸 i 進行求和以消除它。

如果將（1）和（2）放在一起，您將得到經典的內積。

代碼：

# broken
M = np.einsum('i->i', A)

現在，假設我們沒有從下標公式中省略i，我們將所有a[i]和b[i]相乘，並且不總和除以i：

m = np.einsum('i->i', a)

代碼：

c = np.einsum('i->', a)

這也稱為逐元素乘法（或矩陣的哈達瑪積），通常透過 numpy 方法 np.multiply 完成。

下標公式還有第三種變體，稱為外積。

c = 0
I = len(a)
for i in range(I):
   c += a[i]

在此下標公式中，a 和 b 的軸綁定到單獨的字母，因此被視為單獨的「循環變數」。 因此，C 對所有 i 和 j 都有條目 a[i] * b[j]，排列成矩陣。

代碼：

c = 0
I,J = A.shape
for i in range(I):
   for j in range(J):
      c += A[i,j]

三個操作數

將外積更進一步，這是一個三操作數版本：

I,J = A.shape
r = np.zeros(I)
for i in range(I):
   for j in range(J):
      r[i] += A[i,j]

我們的三操作數外積的等效 Python 程式碼是：

I,J = A.shape
r = np.zeros(J)
for i in range(I):
   for j in range(J):
      r[j] += A[i,j]

更進一步，沒有什麼可以阻止我們省略軸來對它們求和，除了轉置通過在右側寫ki而不是ik來計算結果->:

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

等效的 Python 程式碼為：

M = np.einsum('ij->ji', A)

現在我希望您可以開始了解如何輕鬆地指定複雜的張量運算。 當我更廣泛地使用 numpy 時，我發現每當我必須實現複雜的張量運算時，我都會使用 np.einsum。

根據我的經驗，np.einsum 讓以後的程式碼閱讀更加容易- 我可以輕鬆地直接從下標讀出上述操作：“三個向量的外積，中間軸相加，最終結果轉置” 。 如果我必須閱讀一系列複雜的 numpy 運算，我可能會發現自己張口結舌。

一個實際的例子

舉一個實際的例子，讓我們實現法學碩士的核心方程，來自經典論文「注意力就是你所需要的」。

等式。 1 描述注意力機制：

我們將把注意力集中在這個字上 $Q{K}^{T}K$KTT >QKT$T\frac{\mathrm{}}{\sqrt{{}_{}}}$dkk> >1

申請起來很簡單。

的 $Q{K}^{T}K$KTT >QKTT

term 表示

m

個查詢與 n

個鍵的點積。 Q 是

m 個 d 維行向量堆疊成矩陣的集合，因此 Q 的形狀為 md。同樣，K 是 n 個 d 維行向量堆疊成矩陣的集合，因此 K 的形狀為 md。 單一 Q 和 K 之間的乘積可寫為： np.einsum('md,nd->mn', Q, K)

請注意，由於我們寫下標方程式的方式，我們避免了在矩陣乘法之前轉置 K！ 所以，這看起來非常簡單 - 事實上，它只是一個傳統的矩陣乘法。 然而，我們還沒有完成。 注意力就是你所需要的使用多頭注意力，這意味著我們確實有k這樣的矩陣乘法在Q矩陣和K矩陣的索引集合上同時發生.

為了讓事情更清楚一些，我們可以將產品重寫為 $Q_i{K}_{}^{K}TQ\_iK\_i^T$Q我 我T

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

. 這表示我們對於 Q 和 K 都有一個額外的軸 i。 更重要的是，如果我們處於訓練環境中，我們可能正在執行批量這樣的多頭注意力操作。 因此大概想要沿著批次軸 b 對一批範例執行操作。 因此，完整的產品將類似於： 我將跳過這裡的圖表，因為我們正在處理 4 軸張量。 但是您也許可以想像「堆疊」早期的圖表以獲得我們的多頭軸 i，然後「堆疊」這些「堆疊」以獲得我們的批次軸 b。 我很難理解如何使用其他 numpy 方法的任意組合來實現這樣的操作。 然而，經過一些檢查，就很清楚發生了什麼事：在一個批次中，在矩陣 Q 和 K 的集合上，執行矩陣乘法 Qt(K). 現在，這不是很棒嗎？ 無恥的插頭 在創辦人模式磨練了一年之後，我正在找工作。 我在各種技術領域和程式語言方面擁有超過 15 年的經驗，並且還有管理團隊的經驗。 數學和統計學是重點領域。 DM 我，讓我們談談！

以上是numpy&#s einsum 的不合理用處的詳細內容。更多資訊請關注PHP中文網其他相關文章！